はじめに¶
この非常に簡単なケーススタディは、statsmodelsをすぐに使えるようにすることを目的としています。生のデータから始めて、統計モデルを推定し、診断プロットを描くために必要な手順を示します。 statsmodelsまたはその依存関係であるpandasとpatsyによって提供される関数のみを使用します。
モジュールと関数の読み込み¶
statsmodelsとその依存関係をインストールした後、いくつかのモジュールと関数を読み込みます。
In [1]: import statsmodels.api as sm
In [2]: import pandas
In [3]: from patsy import dmatrices
pandasは、numpy配列を基盤として、豊富なデータ構造とデータ分析ツールを提供します。 pandas.DataFrame関数は、Rの「data.frame」と同様に、(潜在的に異種の)データのラベル付き配列を提供します。 pandas.read_csv関数は、カンマ区切り値ファイル(CSV)をDataFrameオブジェクトに変換するために使用できます。
patsyは、Rのような式を使用して統計モデルを記述し、計画行列を構築するためのPythonライブラリです。
注記
この例ではAPIインターフェースを使用しています。APIインターフェース(statsmodels.apiとstatsmodels.tsa.api)をインポートすることと、モデルを定義するモジュールから直接インポートすることの違いについては、インポートパスと構造を参照してください。
データ¶
Andre-Michel Guerryの1833年の著書「フランスの道徳統計に関するエッセイ」を裏付けるために使用された歴史的データのコレクションであるGuerryデータセットをダウンロードします。このデータセットは、Rdatasetsリポジトリによって、カンマ区切り値形式(CSV)でオンラインでホストされています。ファイルをローカルにダウンロードしてread_csvを使用してロードすることもできますが、pandasはこれらすべてを自動的に処理します。
In [4]: df = sm.datasets.get_rdataset("Guerry", "HistData").data
入出力ドキュメントページには、他のさまざまな形式からインポートする方法が示されています。
対象の変数を選択し、下5行を確認します。
In [5]: vars = ['Department', 'Lottery', 'Literacy', 'Wealth', 'Region']
In [6]: df = df[vars]
In [7]: df[-5:]
Out[7]:
Department Lottery Literacy Wealth Region
81 Vienne 40 25 68 W
82 Haute-Vienne 55 13 67 C
83 Vosges 14 62 82 E
84 Yonne 51 47 30 C
85 Corse 83 49 37 NaN
_Region_ 列に1つの欠損値があることに注意してください。 pandasによって提供されるDataFrameメソッドを使用して、それを削除します。
In [8]: df = df.dropna()
In [9]: df[-5:]
Out[9]:
Department Lottery Literacy Wealth Region
80 Vendee 68 28 56 W
81 Vienne 40 25 68 W
82 Haute-Vienne 55 13 67 C
83 Vosges 14 62 82 E
84 Yonne 51 47 30 C
実質的な動機とモデル¶
フランスの86の県の識字率が、1820年代の宝くじの1人当たりの賭け金に関連しているかどうかを知りたいと考えています。各県の富の水準を制御する必要があり、また、回帰方程式の右辺に一連のダミー変数を含めて、地域効果による観測されない異質性を制御したいと考えています。モデルは、最小二乗法回帰(OLS)を使用して推定されます。
計画行列(_endog_と_exog_)¶
statsmodelsで扱われているほとんどのモデルを適合させるには、2つの計画行列を作成する必要があります。1つ目は、内生変数(つまり、従属変数、応答変数、被説明変数など)の行列です。2つ目は、外生変数(つまり、独立変数、予測変数、説明変数など)の行列です。OLS係数推定値は、通常どおり計算されます。
ここで、\(y\)は、1人当たりの宝くじ賭け金(_Lottery_)に関するデータの\(N \times 1\)列です。 \(X\)は、切片、_Literacy_変数と_Wealth_変数、および4つの地域二元変数を持つ\(N \times 7\)です。
patsyモジュールは、Rのような式を使用して計画行列を準備するための便利な関数を備えています。詳細については、こちらをご覧ください。
patsyのdmatrices関数を使用して計画行列を作成します。
In [10]: y, X = dmatrices('Lottery ~ Literacy + Wealth + Region', data=df, return_type='dataframe')
結果の行列/データフレームは次のようになります。
In [11]: y[:3]
Out[11]:
Lottery
0 41.0
1 38.0
2 66.0
In [12]: X[:3]
Out[12]:
Intercept Region[T.E] Region[T.N] ... Region[T.W] Literacy Wealth
0 1.0 1.0 0.0 ... 0.0 37.0 73.0
1 1.0 0.0 1.0 ... 0.0 51.0 22.0
2 1.0 0.0 0.0 ... 0.0 13.0 61.0
[3 rows x 7 columns]
dmatricesは、
カテゴリ変数_Region_を一連の指示変数に分割しました。
外生説明変数行列に定数項を追加しました。
単純なnumpy配列ではなく、
pandasDataFramesを返しました。これは、DataFramesによってstatsmodelsが結果を報告する際にメタデータ(例:変数名)を引き継ぐことができるため便利です。
上記の動作はもちろん変更できます。 patsyドキュメントページを参照してください。
モデルの適合とサマリー¶
statsmodelsでのモデルの適合は、通常3つの簡単な手順で行います。
モデルクラスを使用してモデルを記述する
クラスメソッドを使用してモデルを適合させる
サマリーメソッドを使用して結果を検査する
OLSの場合、これは次のように実現されます。
In [13]: mod = sm.OLS(y, X) # Describe model
In [14]: res = mod.fit() # Fit model
In [15]: print(res.summary()) # Summarize model
OLS Regression Results
==============================================================================
Dep. Variable: Lottery R-squared: 0.338
Model: OLS Adj. R-squared: 0.287
Method: Least Squares F-statistic: 6.636
Date: Thu, 03 Oct 2024 Prob (F-statistic): 1.07e-05
Time: 16:15:27 Log-Likelihood: -375.30
No. Observations: 85 AIC: 764.6
Df Residuals: 78 BIC: 781.7
Df Model: 6
Covariance Type: nonrobust
===============================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------
Intercept 38.6517 9.456 4.087 0.000 19.826 57.478
Region[T.E] -15.4278 9.727 -1.586 0.117 -34.793 3.938
Region[T.N] -10.0170 9.260 -1.082 0.283 -28.453 8.419
Region[T.S] -4.5483 7.279 -0.625 0.534 -19.039 9.943
Region[T.W] -10.0913 7.196 -1.402 0.165 -24.418 4.235
Literacy -0.1858 0.210 -0.886 0.378 -0.603 0.232
Wealth 0.4515 0.103 4.390 0.000 0.247 0.656
==============================================================================
Omnibus: 3.049 Durbin-Watson: 1.785
Prob(Omnibus): 0.218 Jarque-Bera (JB): 2.694
Skew: -0.340 Prob(JB): 0.260
Kurtosis: 2.454 Cond. No. 371.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
resオブジェクトには、多くの便利な属性があります。たとえば、パラメータ推定値と決定係数R二乗は、次のように入力することで抽出できます。
In [16]: res.params
Out[16]:
Intercept 38.651655
Region[T.E] -15.427785
Region[T.N] -10.016961
Region[T.S] -4.548257
Region[T.W] -10.091276
Literacy -0.185819
Wealth 0.451475
dtype: float64
In [17]: res.rsquared
Out[17]: np.float64(0.337950869192882)
属性の完全なリストについては、dir(res)と入力してください。
詳細と例については、回帰ドキュメントページを参照してください。
診断と仕様テスト¶
statsmodelsでは、さまざまな回帰診断と仕様テストを実行できます。たとえば、線形性に関するレインボーテストを適用します(帰無仮説は、関係が線形として適切にモデル化されていることです)。
In [18]: sm.stats.linear_rainbow(res)
Out[18]: (np.float64(0.847233997615691), np.float64(0.6997965543621644))
確かに、上記で生成された出力はあまり冗長ではありませんが、docstring(また、print(sm.stats.linear_rainbow.__doc__))を読むと、最初の数字はF統計量であり、2番目の数字はp値であることがわかります。
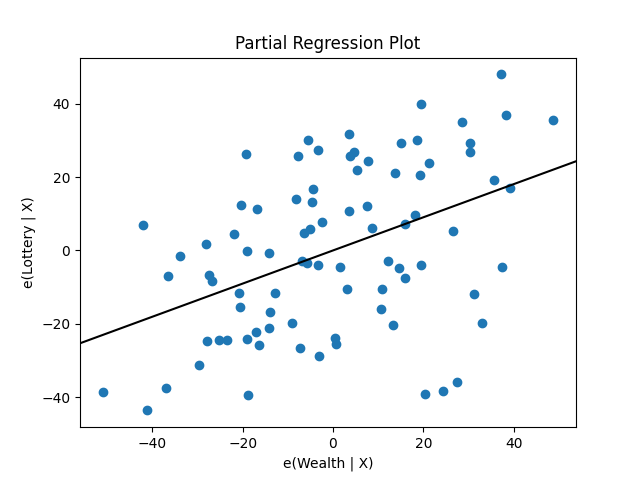
statsmodelsは、グラフィックス関数も提供します。たとえば、一連の 회귀変数 の偏回帰プロットは、次のように描くことができます。
In [19]: sm.graphics.plot_partregress('Lottery', 'Wealth', ['Region', 'Literacy'],
....: data=df, obs_labels=False)
....:
Out[19]: <Figure size 640x480 with 1 Axes>
ドキュメント¶
ドキュメントには、IPythonセッションからwebdocを使用してアクセスできます。
ブラウザを開いてオンラドキュメントを表示します |
その他¶
おめでとうございます! 目次の他のトピックに進む準備ができました。