ベクトル自己回帰 `tsa.vector_ar`¶

statsmodels.tsa.vector_ar には、ベクトル自己回帰 (VAR) とベクトル誤差修正モデル (VECM) を使用して、複数の時系列を同時にモデル化および分析するのに役立つメソッドが含まれています。

VAR(p)過程¶

観測値の数 \(T\) と変数の数 \(K\) の多変量時系列 \(Y\) をモデル化することに関心があります。時系列とそのラグ値間の関係を推定する1つの方法は、ベクトル自己回帰過程です。

\[ \begin{align}\begin{aligned}Y_t = \nu + A_1 Y_{t-1} + \ldots + A_p Y_{t-p} + u_t\\u_t \sim {\sf Normal}(0, \Sigma_u)\end{aligned}\end{align} \]

ここで、\(A_i\) は \(K \times K\) の係数行列です。

私たちは、Lutkepohl (2005) の方法と表記法を大部分踏襲しますが、ここでは詳しく説明しません。

モデル適合¶

注記

以下で参照されているクラスは、statsmodels.tsa.api モジュールからアクセスできます。

VARモデルを推定するには、まず、同種のdtypeまたは構造化されたdtypeのndarrayを使用してモデルを作成する必要があります。構造化配列またはレコード配列を使用する場合、クラスは渡された変数名を使用します。それ以外の場合は、明示的に渡すことができます。

# some example data
In [1]: import numpy as np

In [2]: import pandas

In [3]: import statsmodels.api as sm

In [4]: from statsmodels.tsa.api import VAR

In [5]: mdata = sm.datasets.macrodata.load_pandas().data

# prepare the dates index
In [6]: dates = mdata[['year', 'quarter']].astype(int).astype(str)

In [7]: quarterly = dates["year"] + "Q" + dates["quarter"]

In [8]: from statsmodels.tsa.base.datetools import dates_from_str

In [9]: quarterly = dates_from_str(quarterly)

In [10]: mdata = mdata[['realgdp','realcons','realinv']]

In [11]: mdata.index = pandas.DatetimeIndex(quarterly)

In [12]: data = np.log(mdata).diff().dropna()

# make a VAR model
In [13]: model = VAR(data)

注記

VAR クラスは、渡された時系列が定常であると仮定します。非定常データまたはトレンドのあるデータは、多くの場合、最初に差分をとるなどの方法で定常になるように変換できます。非定常時系列の直接分析には、標準的な安定したVAR(p)モデルは適切ではありません。

実際に推定を行うには、目的のラグ次数でfitメソッドを呼び出します。または、モデルが標準的な情報基準に基づいてラグ次数を選択することもできます（下記参照）。

In [14]: results = model.fit(2)

In [15]: results.summary()
Out[15]: 
  Summary of Regression Results   
==================================
Model:                         VAR
Method:                        OLS
Date:           Thu, 03, Oct, 2024
Time:                     16:15:42
--------------------------------------------------------------------
No. of Equations:         3.00000    BIC:                   -27.5830
Nobs:                     200.000    HQIC:                  -27.7892
Log likelihood:           1962.57    FPE:                7.42129e-13
AIC:                     -27.9293    Det(Omega_mle):     6.69358e-13
--------------------------------------------------------------------
Results for equation realgdp
==============================================================================
                 coefficient       std. error           t-stat            prob
------------------------------------------------------------------------------
const               0.001527         0.001119            1.365           0.172
L1.realgdp         -0.279435         0.169663           -1.647           0.100
L1.realcons         0.675016         0.131285            5.142           0.000
L1.realinv          0.033219         0.026194            1.268           0.205
L2.realgdp          0.008221         0.173522            0.047           0.962
L2.realcons         0.290458         0.145904            1.991           0.047
L2.realinv         -0.007321         0.025786           -0.284           0.776
==============================================================================

Results for equation realcons
==============================================================================
                 coefficient       std. error           t-stat            prob
------------------------------------------------------------------------------
const               0.005460         0.000969            5.634           0.000
L1.realgdp         -0.100468         0.146924           -0.684           0.494
L1.realcons         0.268640         0.113690            2.363           0.018
L1.realinv          0.025739         0.022683            1.135           0.257
L2.realgdp         -0.123174         0.150267           -0.820           0.412
L2.realcons         0.232499         0.126350            1.840           0.066
L2.realinv          0.023504         0.022330            1.053           0.293
==============================================================================

Results for equation realinv
==============================================================================
                 coefficient       std. error           t-stat            prob
------------------------------------------------------------------------------
const              -0.023903         0.005863           -4.077           0.000
L1.realgdp         -1.970974         0.888892           -2.217           0.027
L1.realcons         4.414162         0.687825            6.418           0.000
L1.realinv          0.225479         0.137234            1.643           0.100
L2.realgdp          0.380786         0.909114            0.419           0.675
L2.realcons         0.800281         0.764416            1.047           0.295
L2.realinv         -0.124079         0.135098           -0.918           0.358
==============================================================================

Correlation matrix of residuals
             realgdp  realcons   realinv
realgdp     1.000000  0.603316  0.750722
realcons    0.603316  1.000000  0.131951
realinv     0.750722  0.131951  1.000000

matplotlibを使用したデータの視覚化方法はいくつかあります。

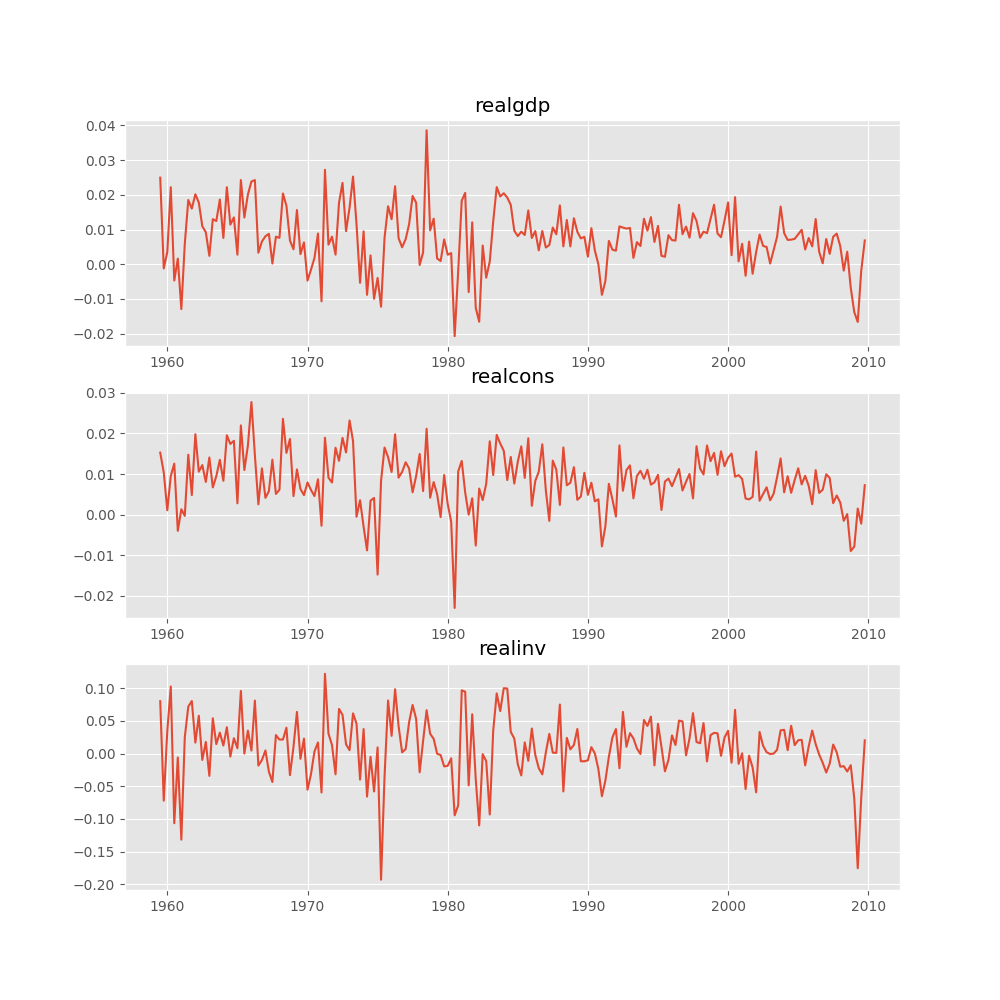
入力時系列のプロット

In [16]: results.plot()
Out[16]: <Figure size 1000x1000 with 3 Axes>

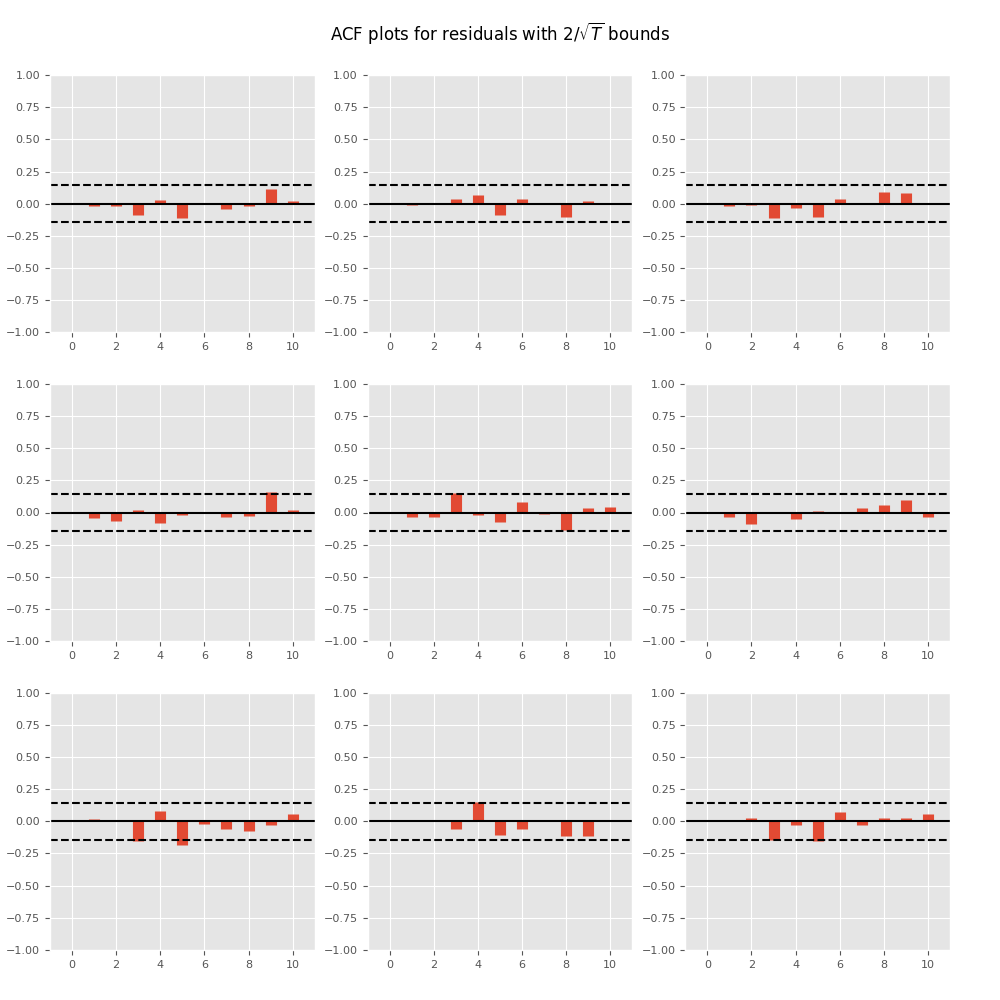
時系列自己相関関数のプロット

In [17]: results.plot_acorr()
Out[17]: <Figure size 1000x1000 with 9 Axes>

ラグ次数選択¶

ラグ次数の選択は難しい問題となる可能性があります。標準的な分析では、尤度検定または情報基準に基づく次数選択が用いられます。後者は、VAR クラスを介してアクセスできます。

In [18]: model.select_order(15)
Out[18]: <statsmodels.tsa.vector_ar.var_model.LagOrderResults at 0x7f18fd4e8430>

fit関数を呼び出す際、最大ラグ数と次数選択に使用する基準を渡すことができます。

In [19]: results = model.fit(maxlags=15, ic='aic')

予測¶

線形予測子は、平均二乗誤差の観点から最適なhステップ先の予測です。

\[y_t(h) = \nu + A_1 y_t(h − 1) + \cdots + A_p y_t(h − p)\]

forecast関数を用いてこの予測を作成できます。予測の「初期値」を指定する必要があることに注意してください。

In [20]: lag_order = results.k_ar

In [21]: results.forecast(data.values[-lag_order:], 5)
Out[21]: 
array([[ 0.0062,  0.005 ,  0.0092],
       [ 0.0043,  0.0034, -0.0024],
       [ 0.0042,  0.0071, -0.0119],
       [ 0.0056,  0.0064,  0.0015],
       [ 0.0063,  0.0067,  0.0038]])

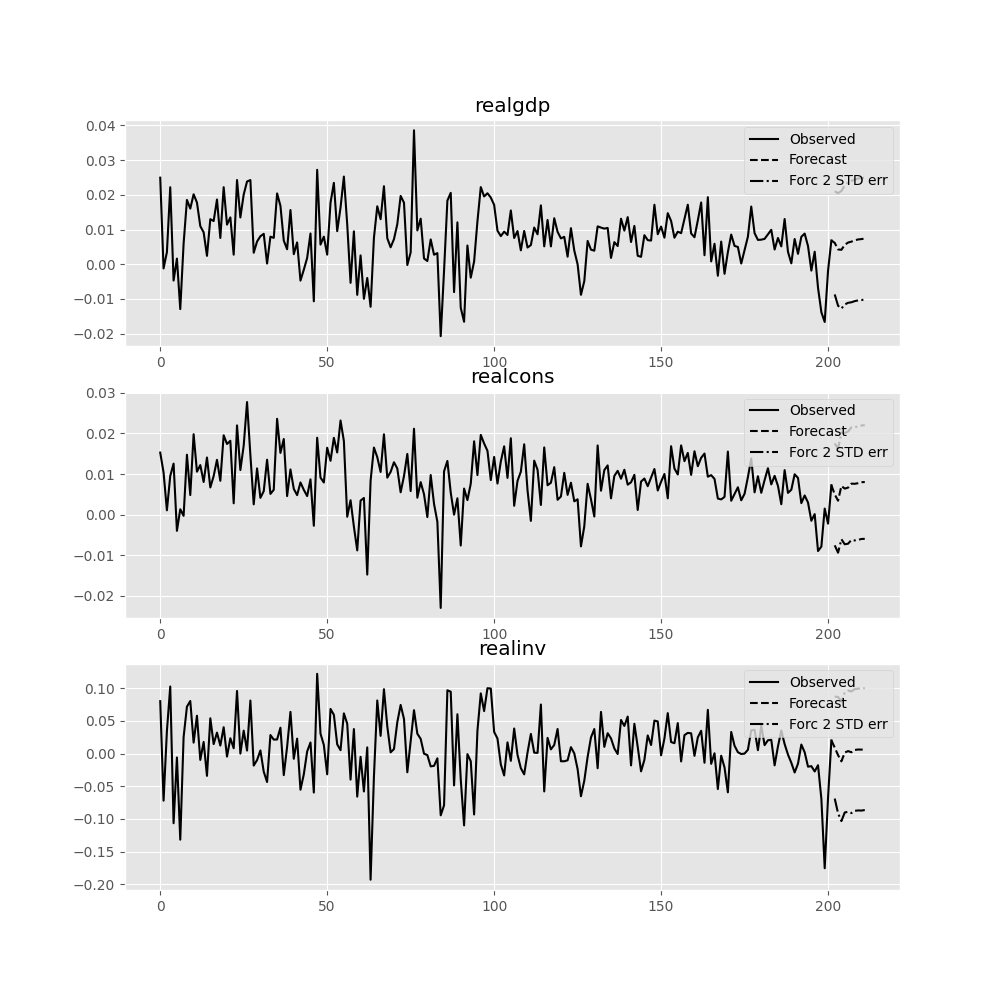
forecast_interval関数は、上記の予測と漸近標準誤差を生成します。これらはplot_forecast関数を用いて視覚化できます。

In [22]: results.plot_forecast(10)
Out[22]: <Figure size 1000x1000 with 3 Axes>

クラスリファレンス¶

`VAR`(endog[, exog, dates, freq, missing])	VAR(p)過程を適合させ、ラグ次数を選択する
`VARProcess`(coefs, coefs_exog, sigma_u[, ...])	既知のVAR(p)過程を表すクラス
`VARResults`(endog, endog_lagged, params, ...)	固定数のラグを持つVAR(p)過程を推定する

推定後分析¶

ベクトル自己回帰過程については、いくつかの過程特性と推定後の追加の結果が利用可能です。

`LagOrderResults`(ics, selected_orders[, vecm])	モデルのラグ次数を選択するための結果クラス。

`HypothesisTestResults`(test_statistic, ...)	仮説検定の結果クラス。
`NormalityTestResults`(test_statistic, ...)	非正規性に対するJarque-Bera検定の結果クラス。
`WhitenessTestResults`(test_statistic, ...)	残差の自己相関に対するPortmanteau検定の結果クラス。

インパルス応答分析¶

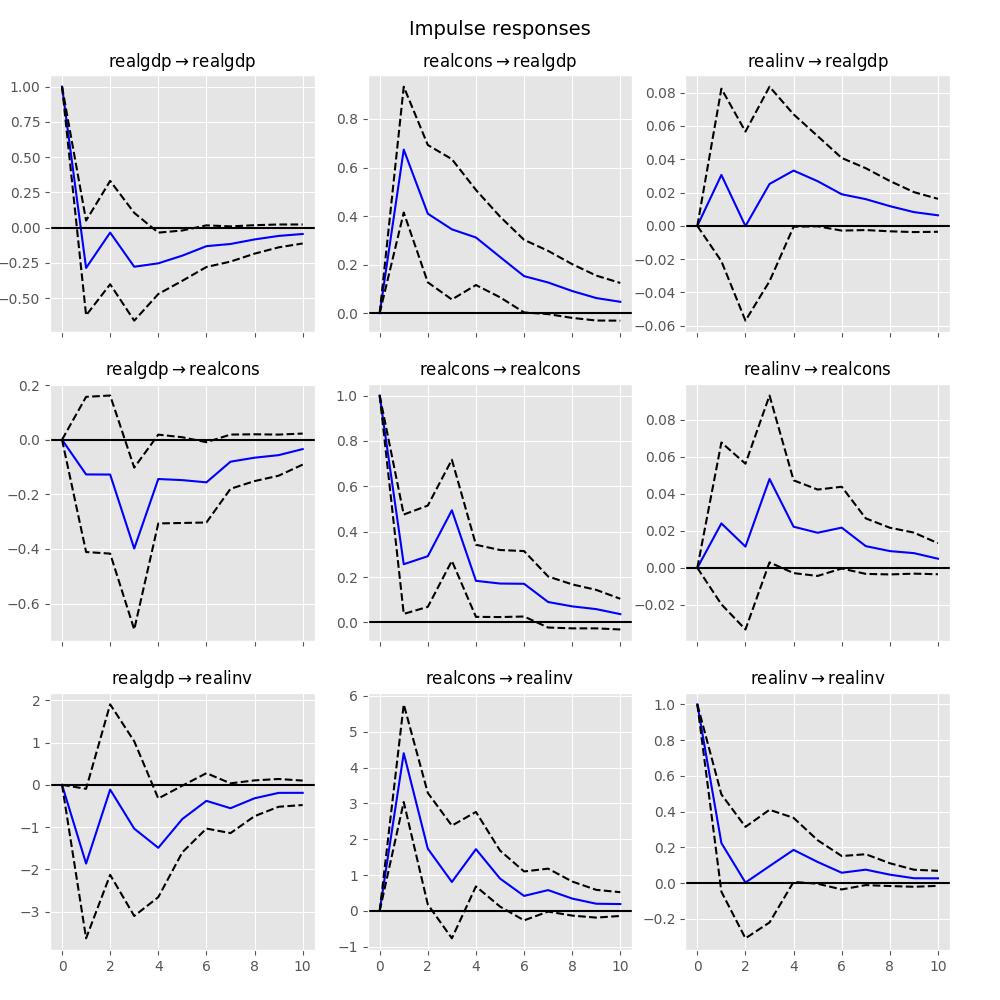
インパルス応答は計量経済学的研究において関心事です。これらは、変数の1つの単位インパルスに対する推定応答です。実際には、VAR(p)過程のMA(\(\infty\))表現を使用して計算されます。

\[Y_t = \mu + \sum_{i=0}^\infty \Phi_i u_{t-i}\]

VARResultsオブジェクトでirf関数を呼び出すことで、インパルス応答分析を実行できます。

In [23]: irf = results.irf(10)

これらはplot関数を用いて、直交化された形式または直交化されていない形式のいずれかで視覚化できます。デフォルトでは、95％の有意水準で漸近標準誤差がプロットされますが、ユーザーが変更できます。

注記

直交化は、推定された誤差共分散行列\(\hat \Sigma_u\)のCholesky分解を使用して行われるため、解釈は変数の順序によって変わる可能性があります。

In [24]: irf.plot(orth=False)
Out[24]: <Figure size 1000x1000 with 9 Axes>

plot関数は柔軟性があり、必要に応じて関心のある変数のみをプロットできます。

In [25]: irf.plot(impulse='realgdp')
Out[25]: <Figure size 1000x1000 with 3 Axes>

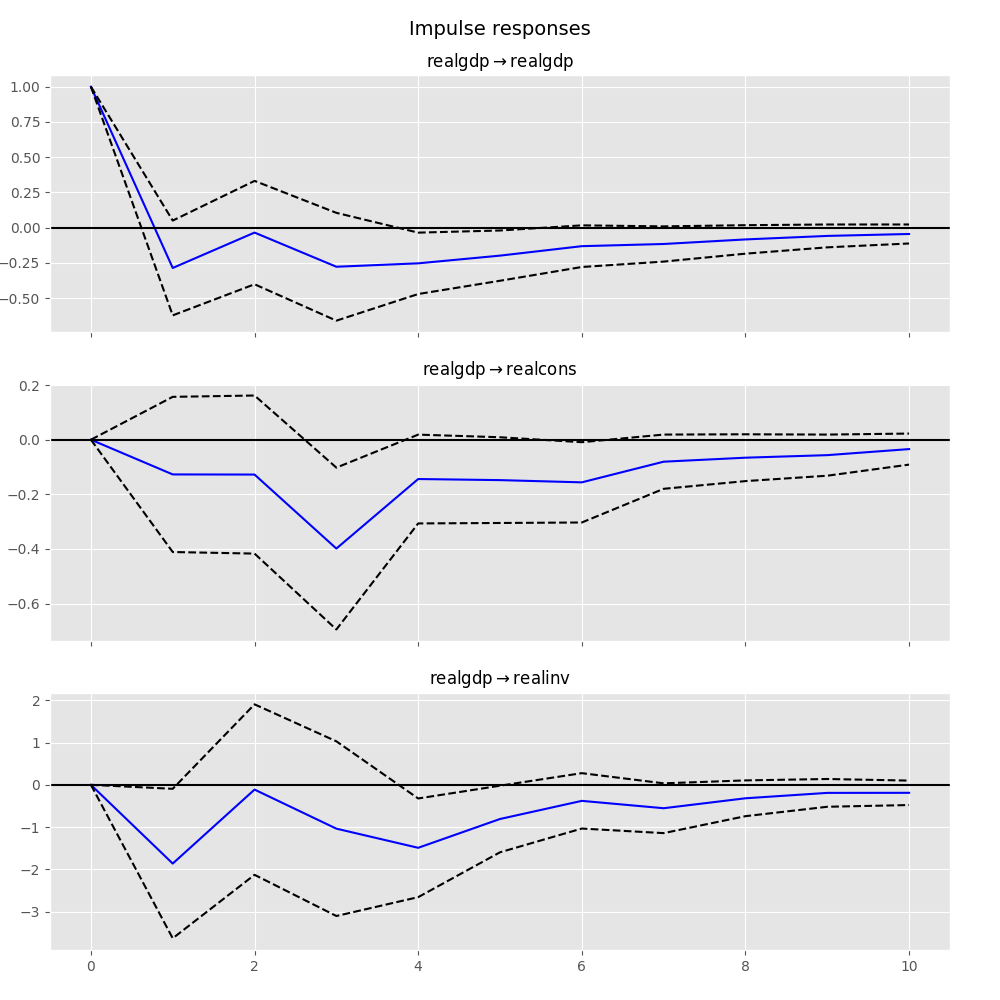
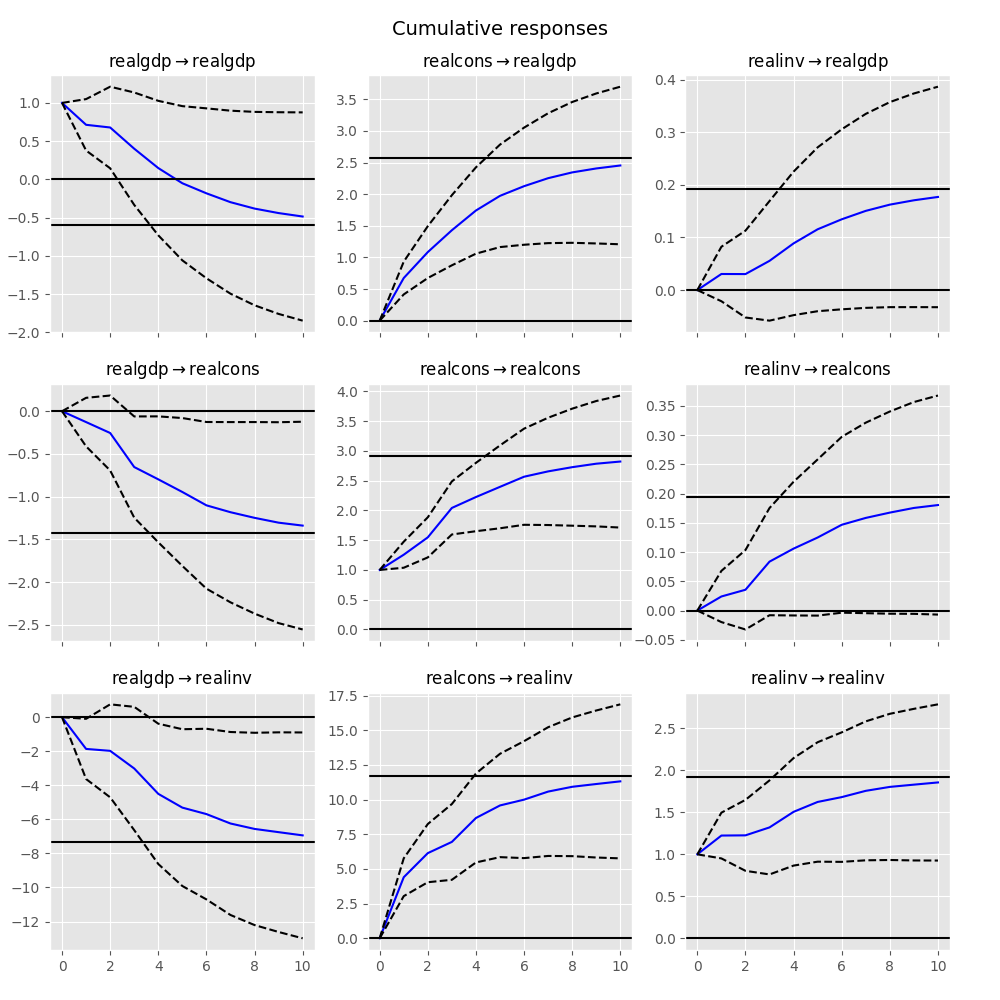
累積効果\(\Psi_n = \sum_{i=0}^n \Phi_i\)は、次のように長期効果と共にプロットできます。

In [26]: irf.plot_cum_effects(orth=False)
Out[26]: <Figure size 1000x1000 with 9 Axes>

`IRAnalysis`(model[, P, periods, order, svar, ...])	インパルス応答分析クラス。

予測誤差分散分解 (FEVD)¶

iステップ先の予測における構成要素jに関する構成要素kの予測誤差は、直交化されたインパルス応答\(\Theta_i\)を使用して分解できます。

\[ \begin{align}\begin{aligned}\omega_{jk, i} = \sum_{i=0}^{h-1} (e_j^\prime \Theta_i e_k)^2 / \mathrm{MSE}_j(h)\\\mathrm{MSE}_j(h) = \sum_{i=0}^{h-1} e_j^\prime \Phi_i \Sigma_u \Phi_i^\prime e_j\end{aligned}\end{align} \]

これらは、fevd関数を使用して、最大ステップ数まで計算されます。

In [27]: fevd = results.fevd(5)

In [28]: fevd.summary()
FEVD for realgdp
      realgdp  realcons   realinv
0    1.000000  0.000000  0.000000
1    0.864889  0.129253  0.005858
2    0.816725  0.177898  0.005378
3    0.793647  0.197590  0.008763
4    0.777279  0.208127  0.014594

FEVD for realcons
      realgdp  realcons   realinv
0    0.359877  0.640123  0.000000
1    0.358767  0.635420  0.005813
2    0.348044  0.645138  0.006817
3    0.319913  0.653609  0.026478
4    0.317407  0.652180  0.030414

FEVD for realinv
      realgdp  realcons   realinv
0    0.577021  0.152783  0.270196
1    0.488158  0.293622  0.218220
2    0.478727  0.314398  0.206874
3    0.477182  0.315564  0.207254
4    0.466741  0.324135  0.209124

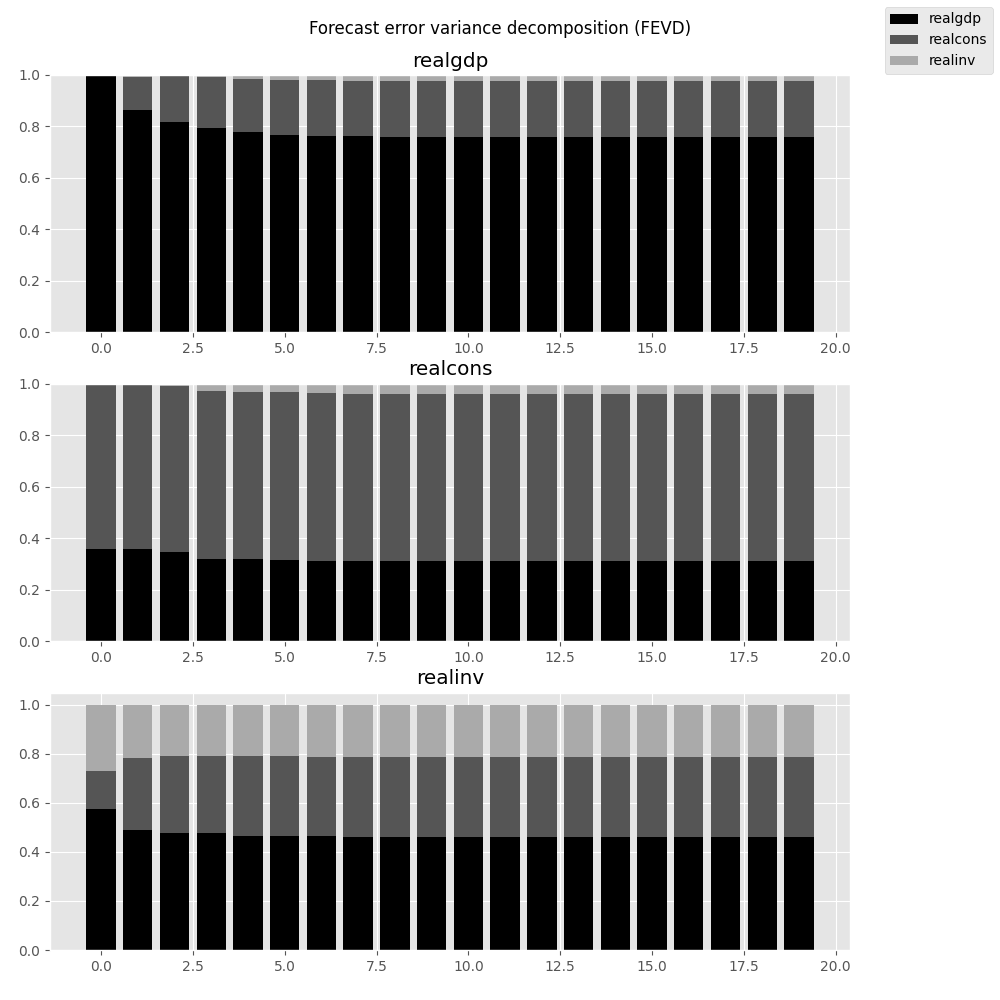
返されるFEVDオブジェクトを使用して視覚化することもできます。

In [29]: results.fevd(20).plot()
Out[29]: <Figure size 1000x1000 with 3 Axes>

`FEVD`(model[, P, periods])	予測誤差分散分解と漸近標準誤差を計算およびプロットします。

統計検定¶

モデルの結果やモデルの仮定の妥当性（正規性、誤差の白色性／「i.i.d.」など）について、さまざまな方法で仮説検定を実行できます。

グレンジャー因果性¶

ある変数または変数のグループが、別の変数に対して「因果的」であるかどうかを、「因果的」の定義によっては、関心を持つことがよくあります。VARモデルの文脈では、ある変数の集合がVAR方程式の1つの中でグレンジャー因果的であると言うことができます。グレンジャー因果性の数学的定義については詳細を述べませんが、読者にお任せします。VARResultsオブジェクトには、ワルド検定（\(\chi^2\)）またはF検定を実行するためのtest_causalityメソッドがあります。

In [30]: results.test_causality('realgdp', ['realinv', 'realcons'], kind='f')
Out[30]: <statsmodels.tsa.vector_ar.hypothesis_test_results.CausalityTestResults at 0x7f18f3daf580>

正規性¶

このドキュメントの冒頭で述べたように、ホワイトノイズ成分\(u_t\)は正規分布していると仮定されています。この仮定は、パラメータ推定値の一致性や漸近的正規性には必要ありませんが、残差がガウスホワイトノイズである場合、有限サンプルでは一般的に結果の信頼性が高まります。この仮定がデータセットと一致するかどうかをテストするために、VARResultsはtest_normalityメソッドを提供しています。

In [31]: results.test_normality()
Out[31]: <statsmodels.tsa.vector_ar.hypothesis_test_results.NormalityTestResults at 0x7f18f3daf640>

残差の白色性¶

推定残差の白色性をテストするには（これは、有意な残差自己相関がないことを意味します）、VARResultsのtest_whitenessメソッドを使用できます。

`HypothesisTestResults`(test_statistic, ...)	仮説検定の結果クラス。
`CausalityTestResults`(causing, caused, ...[, ...])	グレンジャー因果性と瞬間的因果性の結果クラス。
`NormalityTestResults`(test_statistic, ...)	非正規性に対するJarque-Bera検定の結果クラス。
`WhitenessTestResults`(test_statistic, ...)	残差の自己相関に対するPortmanteau検定の結果クラス。

構造ベクトル自己回帰モデル¶

いくつかの種類の構造VARモデルを扱うクラスのセットがあります。

`SVAR`(endog, svar_type[, dates, freq, A, B, ...])	VARを適合させた後、AとBの構造的成分を推定します。
`SVARProcess`(coefs, intercept, sigma_u, ...)	既知のSVAR(p)過程を表すクラス
`SVARResults`(endog, endog_lagged, params, ...)	固定数のラグを持つVAR(p)過程を推定する

ベクトル誤差修正モデル (VECM)¶

ベクトル誤差修正モデルは、1つ以上の永続的な確率的トレンド（単位根）からの短期的なずれを研究するために使用されます。VECMは、仮定された確率的トレンドの数によって暗示される構造を課すことで、時系列ベクトルの差をモデル化します。VECMは、これらのモデルを指定して推定するために使用されます。

VECM(\(k_{ar}-1\))は、次の形式を持ちます。

\[\Delta y_t = \Pi y_{t-1} + \Gamma_1 \Delta y_{t-1} + \ldots + \Gamma_{k_{ar}-1} \Delta y_{t-k_{ar}+1} + u_t\]

ここで

\[\Pi = \alpha \beta'\]

は、[1]の7章で説明されています。

決定論的項を含むVECM(\(k_{ar} - 1\))は、次の形式を持ちます。

\[\begin{split}\Delta y_t = \alpha \begin{pmatrix}\beta' & \eta'\end{pmatrix} \begin{pmatrix}y_{t-1} \\ D^{co}_{t-1}\end{pmatrix} + \Gamma_1 \Delta y_{t-1} + \dots + \Gamma_{k_{ar}-1} \Delta y_{t-k_{ar}+1} + C D_t + u_t.\end{split}\]

\(D^{co}_{t-1}\)には、共和分関係内にある（または共和分関係に制限される）決定論的項が含まれています。\(\eta\)は対応する推定量です。共和分関係内に決定論的項を渡すには、exog_coint引数を使用できます。切片と線形トレンドの2つの特別なケースでは、これらの項を宣言するより簡単な方法があります。deterministic引数にそれぞれ"ci"と"li"を渡すことができます。したがって、共和分関係内の切片の場合、deterministicとして"ci"を渡すか、dataがendog引数として渡された場合、exog_cointとしてnp.ones(len(data))を渡すことができます。これは、すべての\(t\)に対して\(D_{t-1}^{co} = 1\)であることを保証します。

共和分関係の外側の決定論的項も使用できます。これらは、上記の式で\(D_t\)で定義され、行列\(C\)に対応する推定量があります。このような項を指定するには、exog引数に渡します。切片および／または線形トレンドの場合、deterministicを代わりに使用することもできます。切片の場合、"co"を渡し、線形トレンドの場合、"lo"を渡します。ここで、oはoutsideを表します。

[2]で考慮されている5つのケースを示す表を次に示します。最後の列は、これらの各ケースのdeterministic引数に渡す文字列を示しています。

ケース	切片	線形トレンドの傾き	deterministic
I	0	0	`"nc"`
II	\(- \alpha \beta^T \mu\)	0	`"ci"`
III	\(\neq 0\)	0	`"co"`
IV	\(\neq 0\)	\(- \alpha \beta^T \gamma\)	`"coli"`
V	\(\neq 0\)	\(\neq 0\)	`"colo"`

`VECM`(endog[, exog, exog_coint, dates, freq, ...])	ベクトル誤差修正モデル (VECM) を表すクラス。
`coint_johansen`(endog, det_order, k_ar_diff)	VECMの共和分階数のヨハンセン共和分検定
`JohansenTestResult`(rkt, r0t, eig, evec, lr1, ...)	ヨハンセン共和分検定の結果クラス
`select_order`(data, maxlags[, deterministic, ...])	使用可能な情報基準に基づいてラグ次数を選択計算します。
`select_coint_rank`(endog, det_order, k_ar_diff)	VECMの共和分階数を計算します。
`VECMResults`(endog, exog, exog_coint, k_ar, ...)	ベクトル誤差修正モデル (VECM) の推定関連の結果を保持するクラス。
`CointRankResults`(rank, neqs, test_stats, ...)	共和分階数の検定結果を保持するクラス。

参考文献¶

最終更新日：2024年10月3日

ベクトル自己回帰 tsa.vector_ar¶

VAR(p)過程¶

モデル適合¶

ラグ次数選択¶

予測¶

クラスリファレンス¶

推定後分析¶

インパルス応答分析¶

予測誤差分散分解 (FEVD)¶

統計検定¶

グレンジャー因果性¶

正規性¶

残差の白色性¶

構造ベクトル自己回帰モデル¶

ベクトル誤差修正モデル (VECM)¶

参考文献¶

ベクトル自己回帰 `tsa.vector_ar`¶