GLMロジットの影響度指標¶

これは、GLMInfluenceのドラフト版に基づいており、離散ロジット、プロビット、ポアソンにも適用され、最終的には時系列分析以外のほとんどのモデルをカバーするように拡張される予定です。

ロジスティック回帰の例は、Pregibon (1981) の「ロジスティック回帰診断」で使用されており、Finney (1947) のデータに基づいています。

GLMInfluenceには基本的な影響度指標が含まれていますが、Pregibon (1981) で説明されている指標、例えば、逸脱度や信頼区間への影響に関連する指標はまだ含まれていません。

[1]:

import os.path
import pandas as pd
import matplotlib.pyplot as plt

from statsmodels.genmod.generalized_linear_model import GLM
from statsmodels.genmod import families

plt.rc("figure", figsize=(16, 8))
plt.rc("font", size=14)

[2]:

import statsmodels.stats.tests.test_influence

test_module = statsmodels.stats.tests.test_influence.__file__
cur_dir = cur_dir = os.path.abspath(os.path.dirname(test_module))

file_name = "binary_constrict.csv"
file_path = os.path.join(cur_dir, "results", file_name)
df = pd.read_csv(file_path, index_col=0)

[3]:

res = GLM(
    df["constrict"],
    df[["const", "log_rate", "log_volumne"]],
    family=families.Binomial(),
).fit(attach_wls=True, atol=1e-10)
print(res.summary())

                 Generalized Linear Model Regression Results
==============================================================================
Dep. Variable:              constrict   No. Observations:                   39
Model:                            GLM   Df Residuals:                       36
Model Family:                Binomial   Df Model:                            2
Link Function:                  Logit   Scale:                          1.0000
Method:                          IRLS   Log-Likelihood:                -14.614
Date:                Thu, 03 Oct 2024   Deviance:                       29.227
Time:                        15:49:03   Pearson chi2:                     34.2
No. Iterations:                     7   Pseudo R-squ. (CS):             0.4707
Covariance Type:            nonrobust
===============================================================================
                  coef    std err          z      P>|z|      [0.025      0.975]
-------------------------------------------------------------------------------
const          -2.8754      1.321     -2.177      0.029      -5.464      -0.287
log_rate        4.5617      1.838      2.482      0.013       0.959       8.164
log_volumne     5.1793      1.865      2.777      0.005       1.524       8.834
===============================================================================

影響度指標の取得¶

GLMResultsには、OLSResultsと同様に、GLMInfluenceクラスのインスタンスを返すget_influenceメソッドがあります。このクラスには、影響度と外れ値の指標を検査するためのメソッドと（キャッシュされた）属性があります。

これらの指標は、1つの観測値を削除した結果に対する1ステップ近似に基づいています。1ステップ近似は、通常、小さな変化に対しては正確ですが、大きな変化の大きさを過小評価します。大きな変化は過小評価されますが、影響力の強い観測値の影響は明確に示されます。

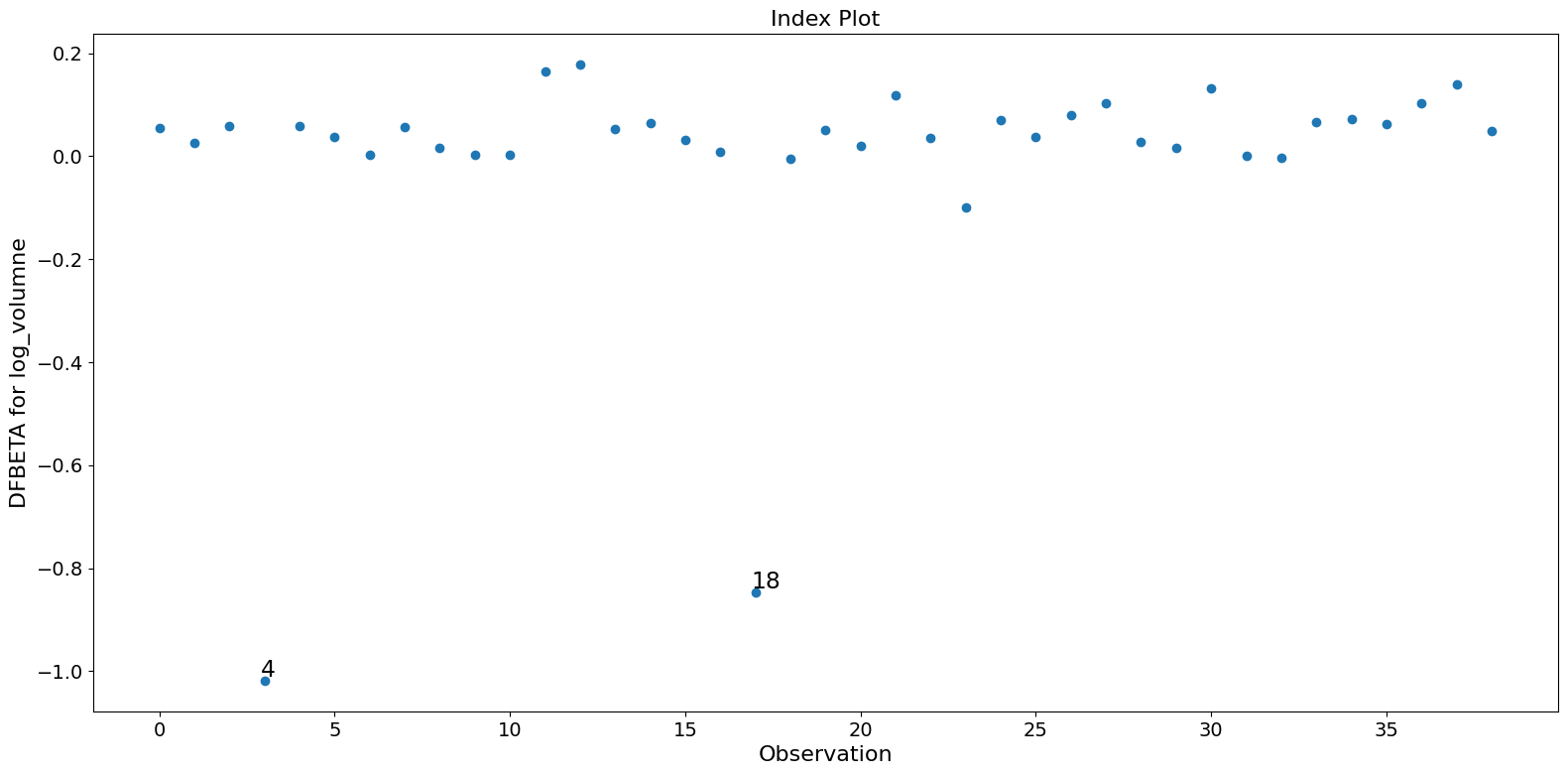
この例では、観測値4と18は大きな標準化残差と大きなクック距離を持っていますが、大きなレバレッジはありません。観測値13は最大のレバレッジを持っていますが、クック距離は小さく、スチューデント化残差も大きくありません。

パラメータ推定に大きな影響を与えるのは、観測値4と18の2つだけです。

[4]:

infl = res.get_influence(observed=False)

[5]:

summ_df = infl.summary_frame()
summ_df.sort_values("cooks_d", ascending=False)[:10]

[5]:

	dfb_const	dfb_log_rate	dfb_log_volumne	cooks_d	standard_resid	hat_diag	dffits_internal
ケース
4	1.073359	-0.930200	-1.017953	0.429085	3.681352	0.086745	1.134573
18	0.959508	-0.827905	-0.847666	0.328152	3.055542	0.095386	0.992197
19	-0.259120	0.202363	-0.004883	0.066770	-1.150095	0.131521	-0.447560
29	0.236747	-0.194984	0.028643	0.065370	0.984729	0.168219	0.442844
31	0.116501	-0.099602	0.132197	0.055382	0.713771	0.245917	0.407609
24	-0.128107	0.041039	-0.100410	0.051950	-1.420261	0.071721	-0.394777
13	-0.093083	-0.009463	0.177532	0.046492	-0.847046	0.162757	-0.373465
23	-0.196119	0.127482	0.035689	0.031168	-1.065576	0.076085	-0.305786
33	-0.088174	-0.013657	-0.002161	0.027481	-1.238185	0.051031	-0.287130
6	-0.092235	0.170980	0.038080	0.026230	0.661478	0.152431	0.280520

[6]:

fig = infl.plot_influence()
fig.tight_layout(pad=1.0)

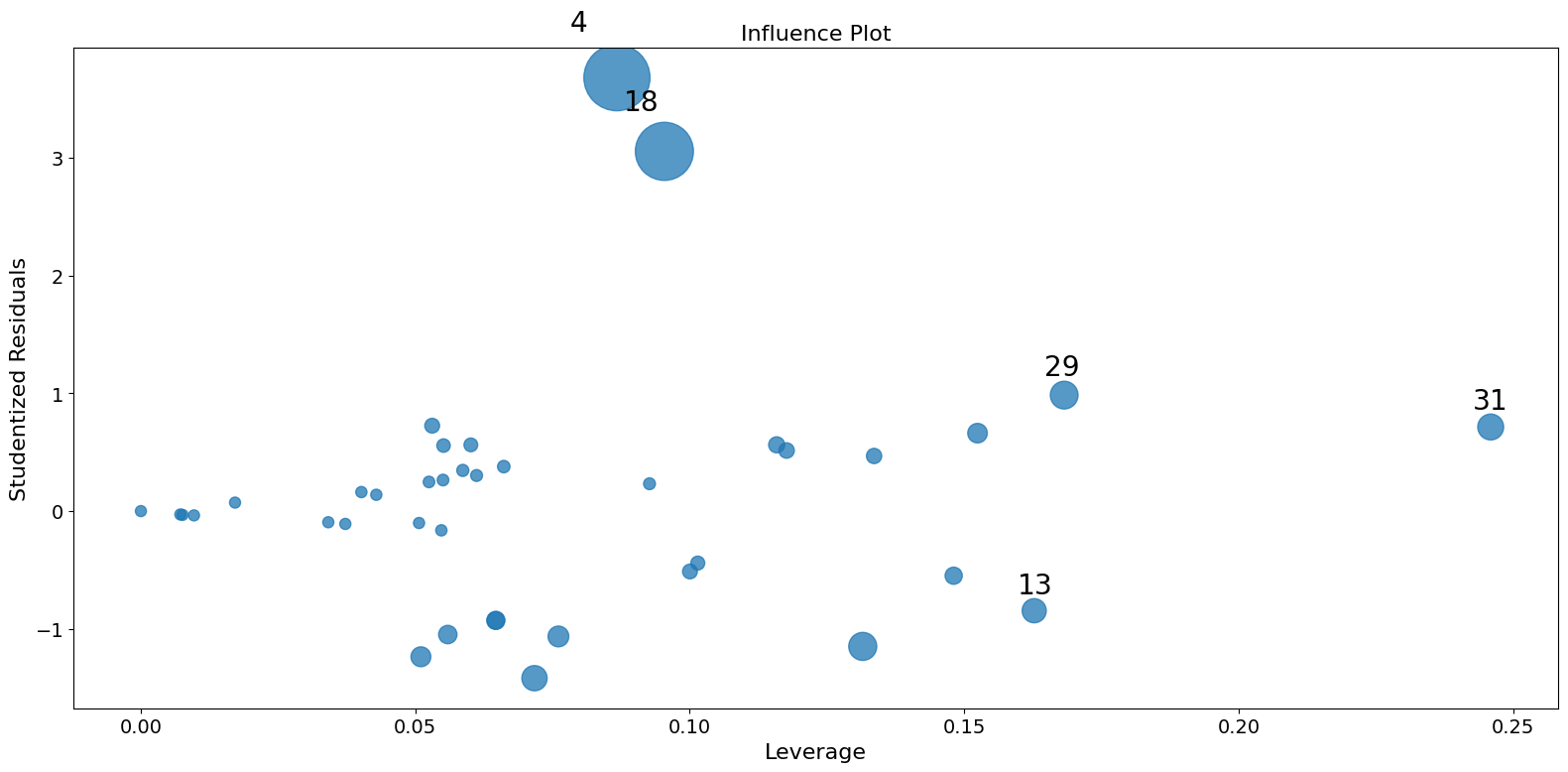
../../../_images/examples_notebooks_generated_influence_glm_logit_7_0.png

[7]:

fig = infl.plot_index(y_var="cooks", threshold=2 * infl.cooks_distance[0].mean())
fig.tight_layout(pad=1.0)

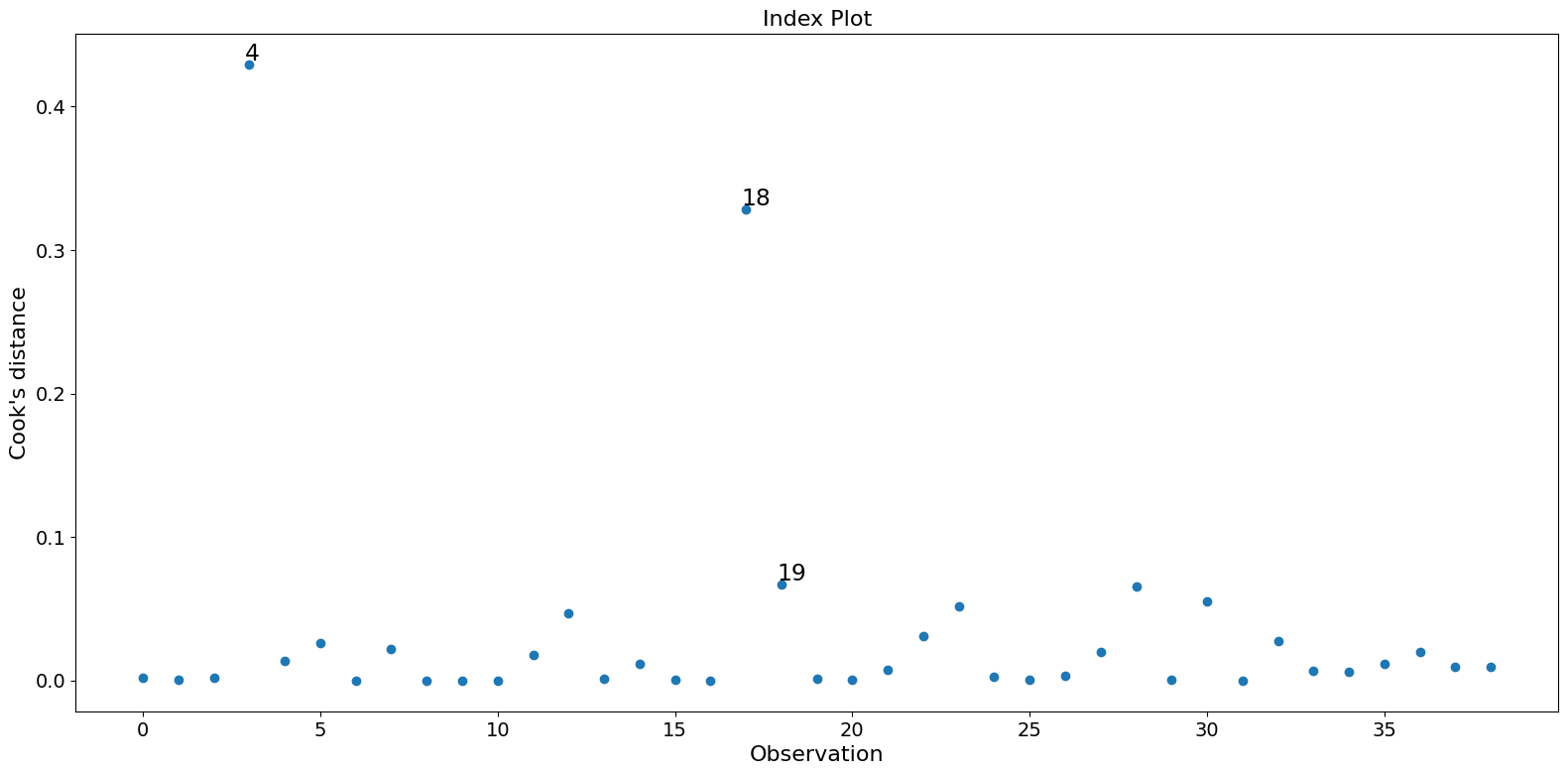
../../../_images/examples_notebooks_generated_influence_glm_logit_8_0.png

[8]:

fig = infl.plot_index(y_var="resid", threshold=1)
fig.tight_layout(pad=1.0)

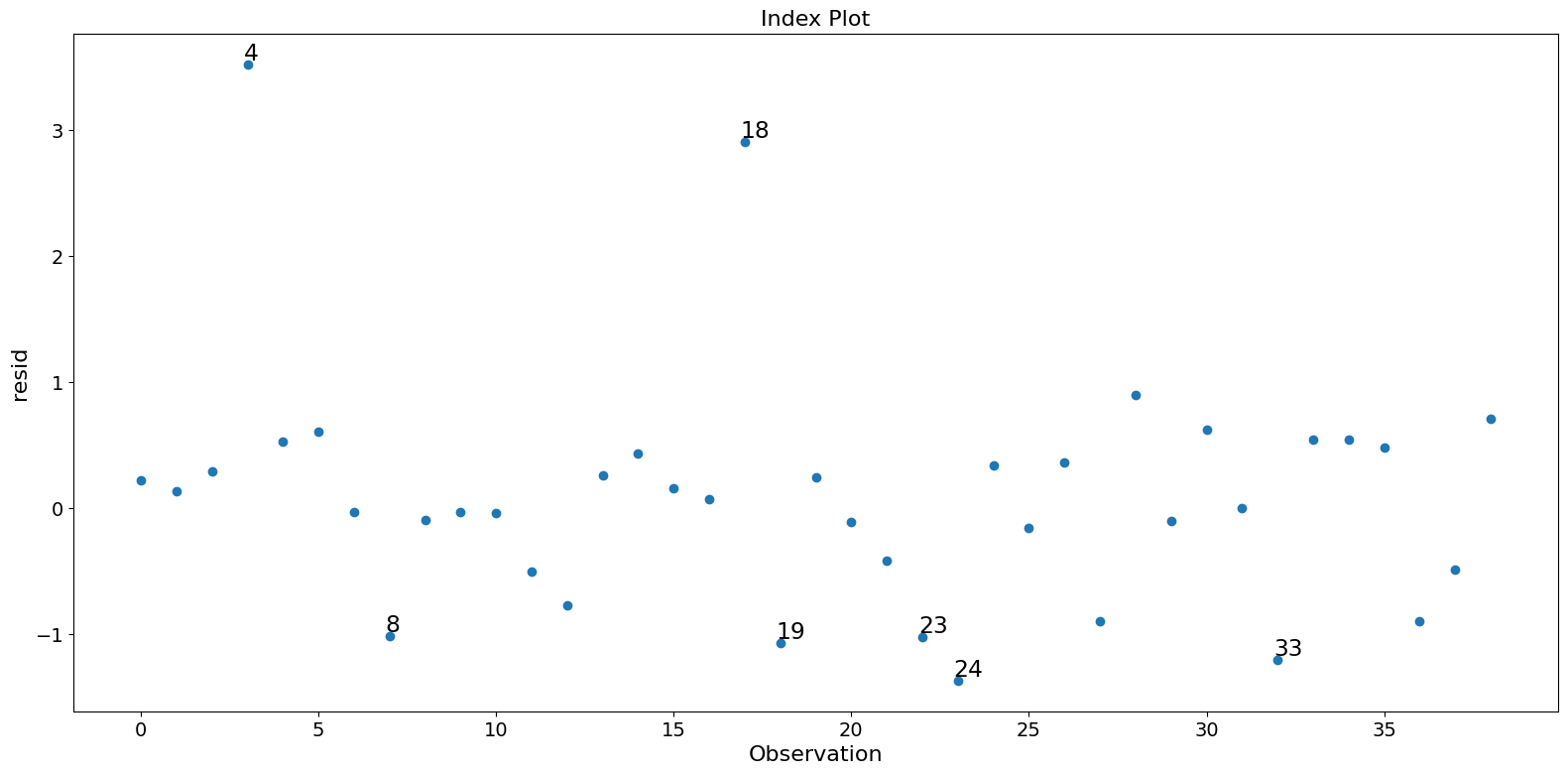
../../../_images/examples_notebooks_generated_influence_glm_logit_9_0.png

[9]:

fig = infl.plot_index(y_var="dfbeta", idx=1, threshold=0.5)
fig.tight_layout(pad=1.0)

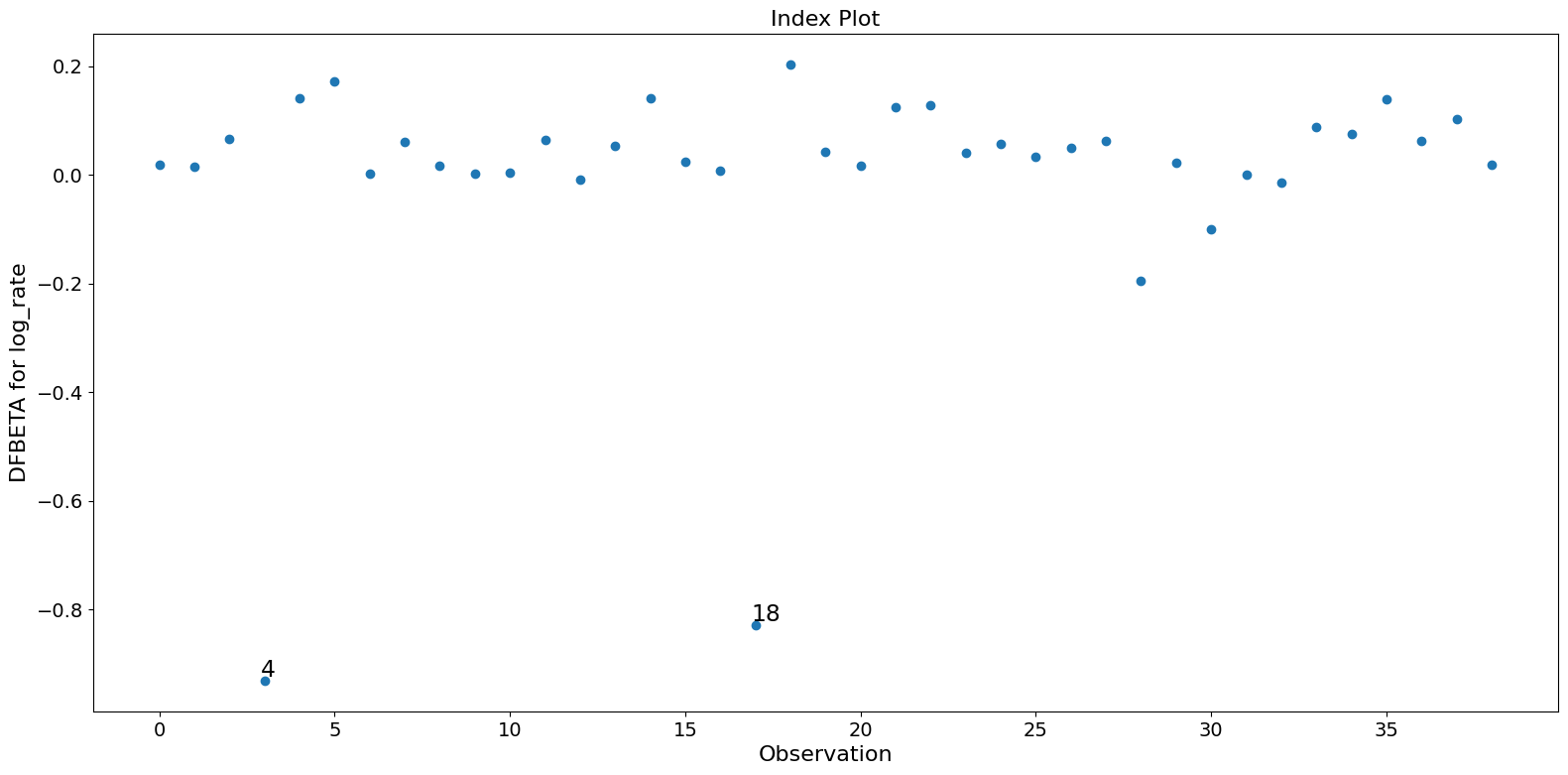
../../../_images/examples_notebooks_generated_influence_glm_logit_10_0.png

[10]:

fig = infl.plot_index(y_var="dfbeta", idx=2, threshold=0.5)
fig.tight_layout(pad=1.0)

../../../_images/examples_notebooks_generated_influence_glm_logit_11_0.png

[11]:

fig = infl.plot_index(y_var="dfbeta", idx=0, threshold=0.5)
fig.tight_layout(pad=1.0)

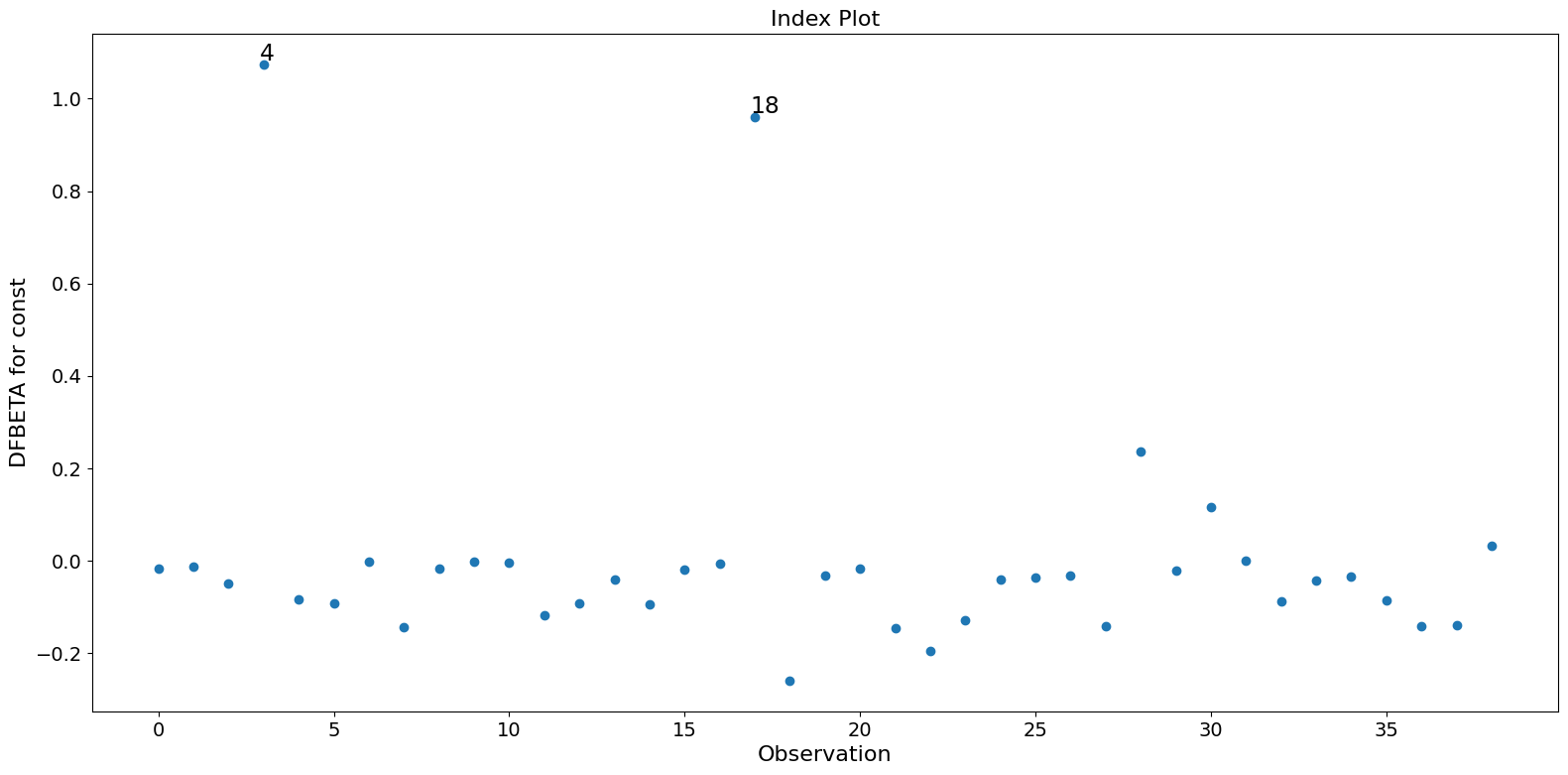
../../../_images/examples_notebooks_generated_influence_glm_logit_12_0.png

[ ]:

最終更新日: 2024年10月3日