statsmodels主成分分析¶
主要な概念: 主成分分析、世界銀行データ、出生率
このノートブックでは、世界銀行から入手したデータを使用して、192か国の出生率の時系列を分析するために主成分分析(PCA)を使用します。主な目的は、時間の経過に伴う出生率の傾向が国によってどのように異なるかを理解することです。これは、データが時系列であるため、PCAのやや非典型的な例です。この設定では機能的PCAなどの手法が開発されていますが、出生率のデータは非常に滑らかであるため、この場合、標準的なPCAを使用することによる実際の欠点はほとんどありません。
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.multivariate.pca import PCA
plt.rc("figure", figsize=(16, 8))
plt.rc("font", size=14)
データは世界銀行のウェブサイトから入手できますが、ここでは、わずかにクリーンアップされたバージョンのデータを使用しています。
[2]:
data = sm.datasets.fertility.load_pandas().data
data.head()
[2]:
| 国名 | 国コード | 指標名 | 指標コード | 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | ... | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | アルバ | ABW | 合計特殊出生率(女性一人当たりの出生数) | SP.DYN.TFRT.IN | 4.820 | 4.655 | 4.471 | 4.271 | 4.059 | 3.842 | ... | 1.786 | 1.769 | 1.754 | 1.739 | 1.726 | 1.713 | 1.701 | 1.690 | NaN | NaN |
| 1 | アンドラ | AND | 合計特殊出生率(女性一人当たりの出生数) | SP.DYN.TFRT.IN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | 1.240 | 1.180 | 1.250 | 1.190 | 1.220 | NaN | NaN | NaN |
| 2 | アフガニスタン | AFG | 合計特殊出生率(女性一人当たりの出生数) | SP.DYN.TFRT.IN | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | ... | 7.136 | 6.930 | 6.702 | 6.456 | 6.196 | 5.928 | 5.659 | 5.395 | NaN | NaN |
| 3 | アンゴラ | AGO | 合計特殊出生率(女性一人当たりの出生数) | SP.DYN.TFRT.IN | 7.316 | 7.354 | 7.385 | 7.410 | 7.425 | 7.430 | ... | 6.704 | 6.657 | 6.598 | 6.523 | 6.434 | 6.331 | 6.218 | 6.099 | NaN | NaN |
| 4 | アルバニア | ALB | 合計特殊出生率(女性一人当たりの出生数) | SP.DYN.TFRT.IN | 6.186 | 6.076 | 5.956 | 5.833 | 5.711 | 5.594 | ... | 2.004 | 1.919 | 1.849 | 1.796 | 1.761 | 1.744 | 1.741 | 1.748 | NaN | NaN |
5行×58列
ここでは、数値の出生率データのみを含むDataFrameを作成し、インデックスを国名に設定します。また、欠損データのある国はすべて削除します。
[3]:
columns = list(map(str, range(1960, 2012)))
data.set_index("Country Name", inplace=True)
dta = data[columns]
dta = dta.dropna()
dta.head()
[3]:
| 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 | ... | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 国名 | |||||||||||||||||||||
| アルバ | 4.820 | 4.655 | 4.471 | 4.271 | 4.059 | 3.842 | 3.625 | 3.417 | 3.226 | 3.054 | ... | 1.825 | 1.805 | 1.786 | 1.769 | 1.754 | 1.739 | 1.726 | 1.713 | 1.701 | 1.690 |
| アフガニスタン | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | 7.671 | ... | 7.484 | 7.321 | 7.136 | 6.930 | 6.702 | 6.456 | 6.196 | 5.928 | 5.659 | 5.395 |
| アンゴラ | 7.316 | 7.354 | 7.385 | 7.410 | 7.425 | 7.430 | 7.422 | 7.403 | 7.375 | 7.339 | ... | 6.778 | 6.743 | 6.704 | 6.657 | 6.598 | 6.523 | 6.434 | 6.331 | 6.218 | 6.099 |
| アルバニア | 6.186 | 6.076 | 5.956 | 5.833 | 5.711 | 5.594 | 5.483 | 5.376 | 5.268 | 5.160 | ... | 2.195 | 2.097 | 2.004 | 1.919 | 1.849 | 1.796 | 1.761 | 1.744 | 1.741 | 1.748 |
| アラブ首長国連邦 | 6.928 | 6.910 | 6.893 | 6.877 | 6.861 | 6.841 | 6.816 | 6.783 | 6.738 | 6.679 | ... | 2.428 | 2.329 | 2.236 | 2.149 | 2.071 | 2.004 | 1.948 | 1.903 | 1.868 | 1.841 |
5行×52列
長方形の行列を分析するためにPCAを使用するには2つの方法があります。行を「オブジェクト」として、列を「変数」として扱うか、その逆を行うことができます。ここでは、国を「オブジェクト」として測定するために使用される「変数」として出生率の測定値を扱います。したがって、目標は、年間出生率の値を、さまざまな国における時間の経過に伴う変化の大部分を捉える少数の出生率「プロファイル」または「基底関数」に削減することです。
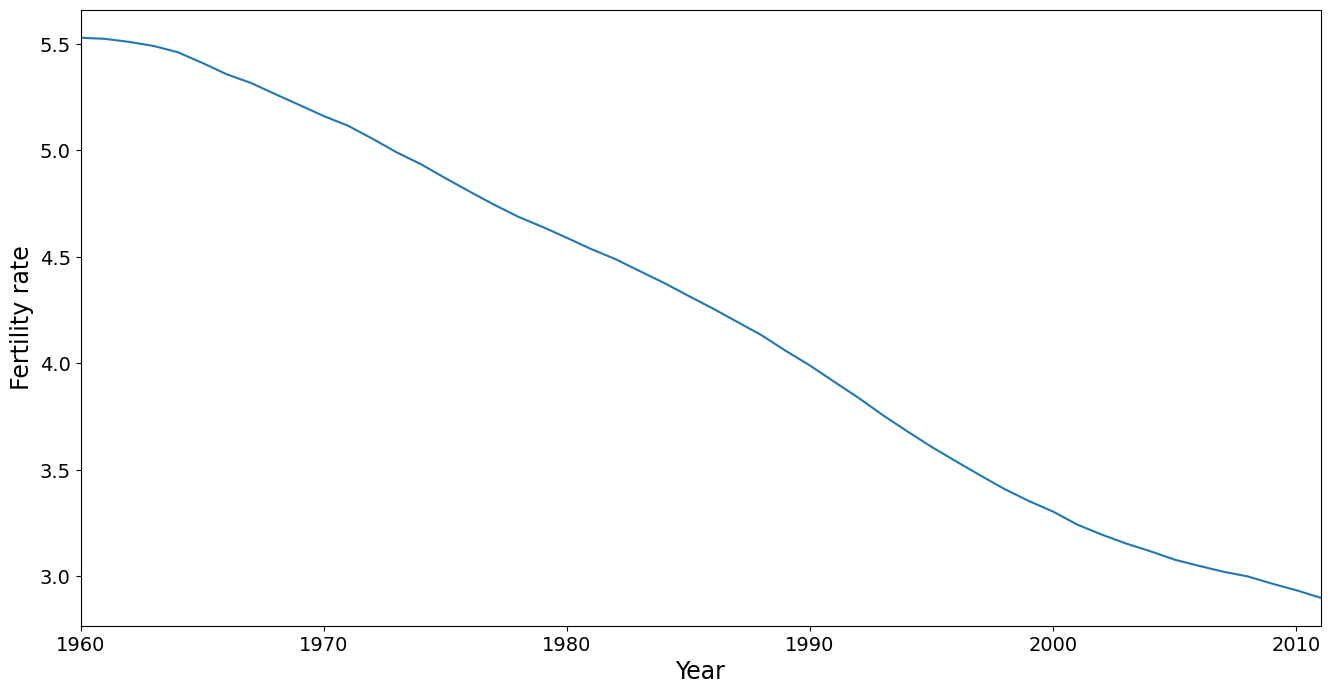
平均トレンドはPCAで削除されますが、それを確認する価値はあります。これにより、このデータセットでカバーされている期間中に出生率が着実に低下していることがわかります。平均は、人口規模を無視して、分析単位として国を使用して計算されていることに注意してください。これは、以下で実施されるPC分析にも当てはまります。より高度な分析では、国に重み付けを行うことができます(たとえば、1980年の人口による)。
[4]:
ax = dta.mean().plot(grid=False)
ax.set_xlabel("Year", size=17)
ax.set_ylabel("Fertility rate", size=17)
ax.set_xlim(0, 51)
[4]:
(0.0, 51.0)
次に、PCAを実行します。
[5]:
pca_model = PCA(dta.T, standardize=False, demean=True)
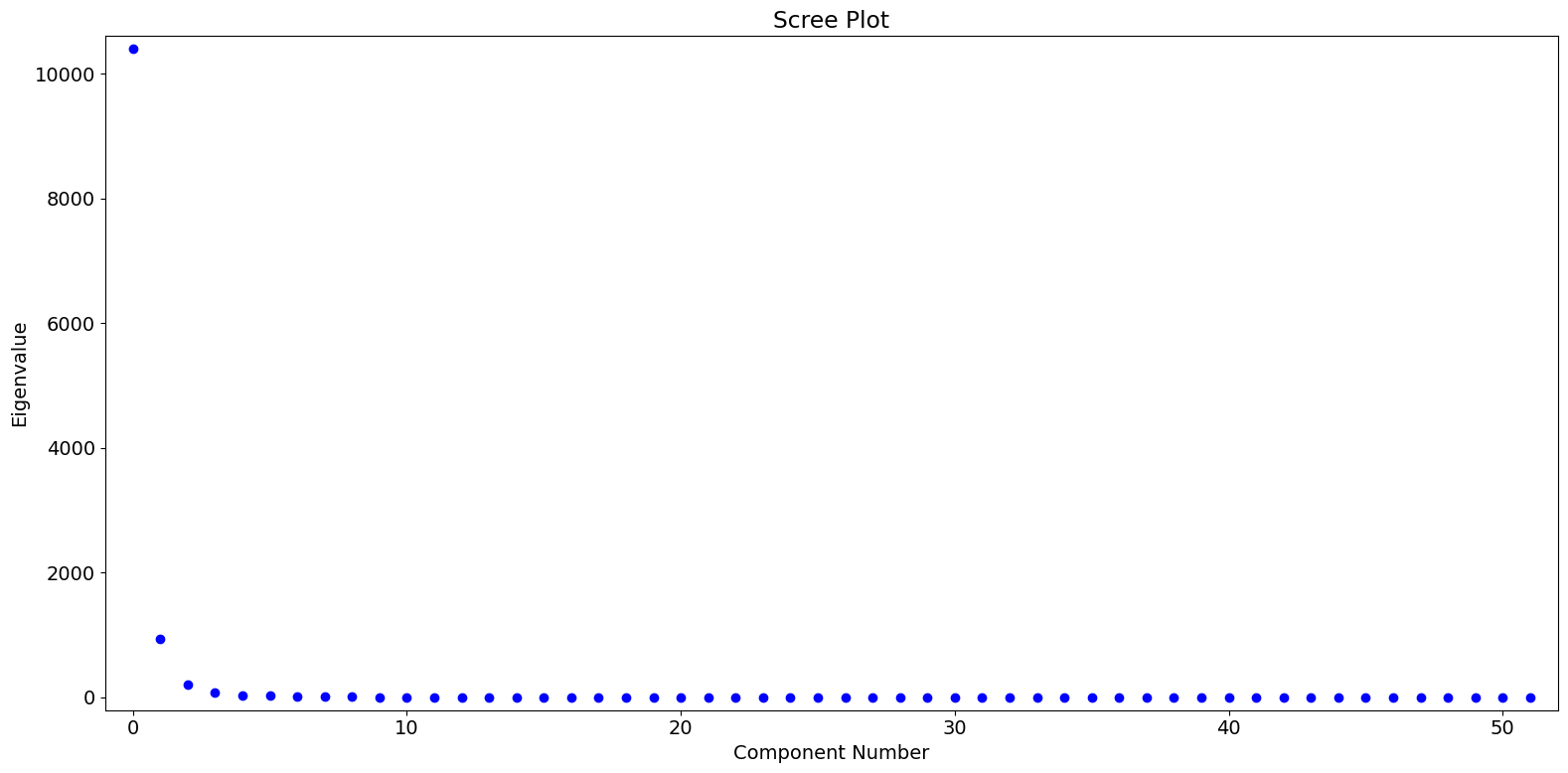
固有値に基づいて、第1のPCが支配的であり、おそらく第2および第3のPCに意味のある変化が少量捉えられていることがわかります。
[6]:
fig = pca_model.plot_scree(log_scale=False)
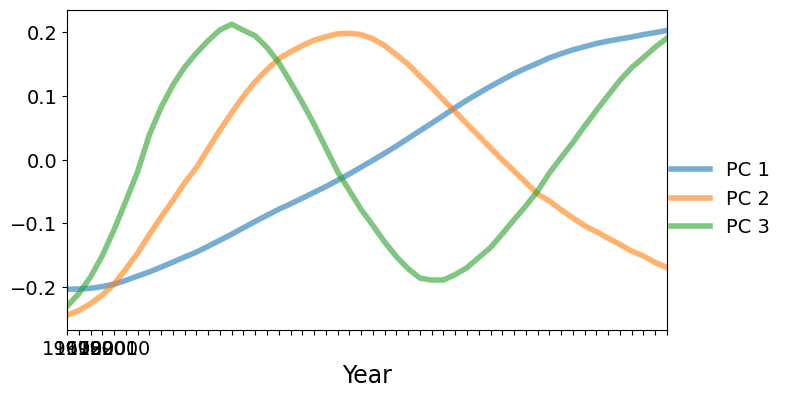
次に、PCファクターをプロットします。支配的なファクターは単調増加です。第1のファクターで正のスコアを持つ国は、上記で示した平均と比較して、より速く増加します(またはよりゆっくりと減少します)。第1のファクターで負のスコアを持つ国は、平均よりも速く減少します。第2のファクターはU字型で、1985年頃に正のピークがあります。第2のファクターで大きな正のスコアを持つ国は、データ範囲の開始時と終了時では平均よりも低い出生率を持ちますが、範囲の中間では平均よりも高い出生率を持ちます。
[7]:
fig, ax = plt.subplots(figsize=(8, 4))
lines = ax.plot(pca_model.factors.iloc[:, :3], lw=4, alpha=0.6)
ax.set_xticklabels(dta.columns.values[::10])
ax.set_xlim(0, 51)
ax.set_xlabel("Year", size=17)
fig.subplots_adjust(0.1, 0.1, 0.85, 0.9)
legend = fig.legend(lines, ["PC 1", "PC 2", "PC 3"], loc="center right")
legend.draw_frame(False)
/tmp/ipykernel_3281/427128218.py:3: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
ax.set_xticklabels(dta.columns.values[::10])
何が起こっているかをよりよく理解するために、同様のPCスコアを持つ国のセットの出生率の軌跡をプロットします。次の便宜的な関数は、そのようなプロットを作成します。
[8]:
idx = pca_model.loadings.iloc[:, 0].argsort()
まず、PC1で最も高いスコアを持つ5つの国をプロットします。これらの国は、世界の平均(減少している)よりも高い出生率増加率を持っています。
[9]:
def make_plot(labels):
fig, ax = plt.subplots(figsize=(9, 5))
ax = dta.loc[labels].T.plot(legend=False, grid=False, ax=ax)
dta.mean().plot(ax=ax, grid=False, label="Mean")
ax.set_xlim(0, 51)
fig.subplots_adjust(0.1, 0.1, 0.75, 0.9)
ax.set_xlabel("Year", size=17)
ax.set_ylabel("Fertility", size=17)
legend = ax.legend(
*ax.get_legend_handles_labels(), loc="center left", bbox_to_anchor=(1, 0.5)
)
legend.draw_frame(False)
[10]:
labels = dta.index[idx[-5:]]
make_plot(labels)
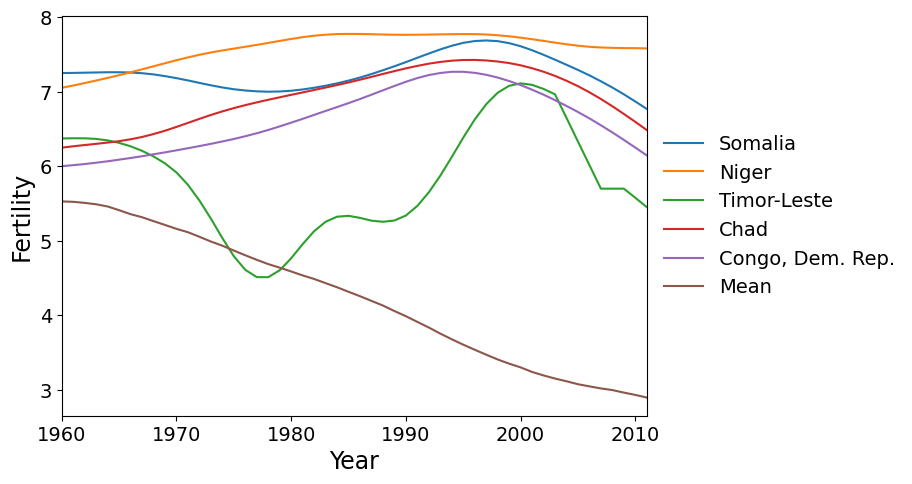
次に、ファクター2で最も高いスコアを持つ5つの国を示します。これらは、世界の他の多くの国よりも遅く、1980年頃にピークの出生率に達し、その後出生率が急速に低下した国です。
[11]:
idx = pca_model.loadings.iloc[:, 1].argsort()
make_plot(dta.index[idx[-5:]])
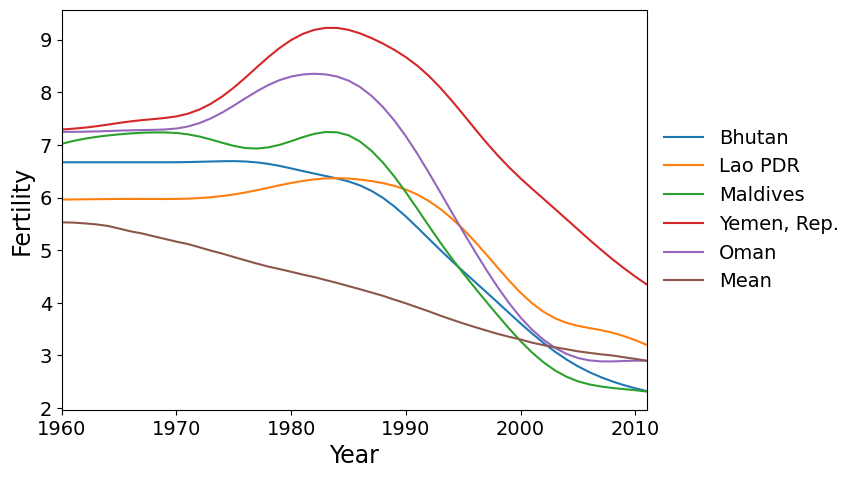
最後に、PC2で最も負のスコアを持つ国があります。これらは、1960年代と1970年代に世界の平均よりもはるかに速く出生率が低下し、その後平坦化した国です。
[12]:
make_plot(dta.index[idx[:5]])
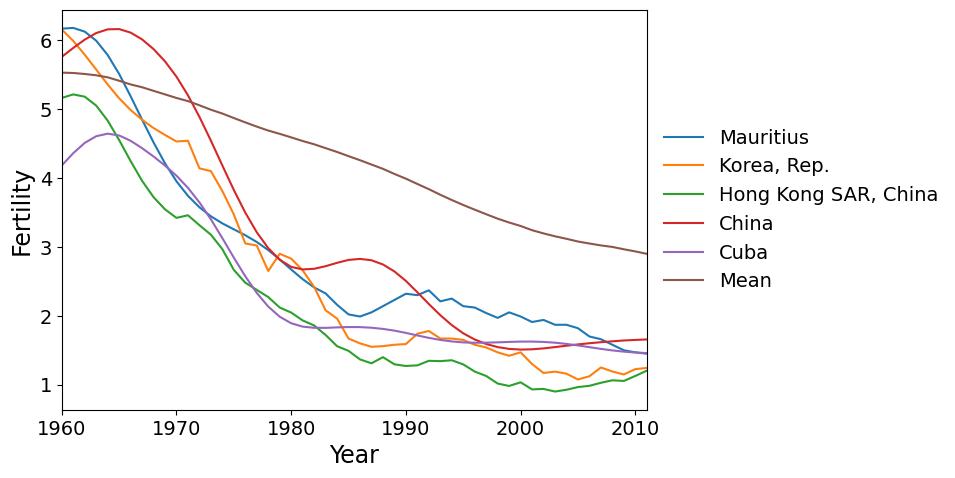
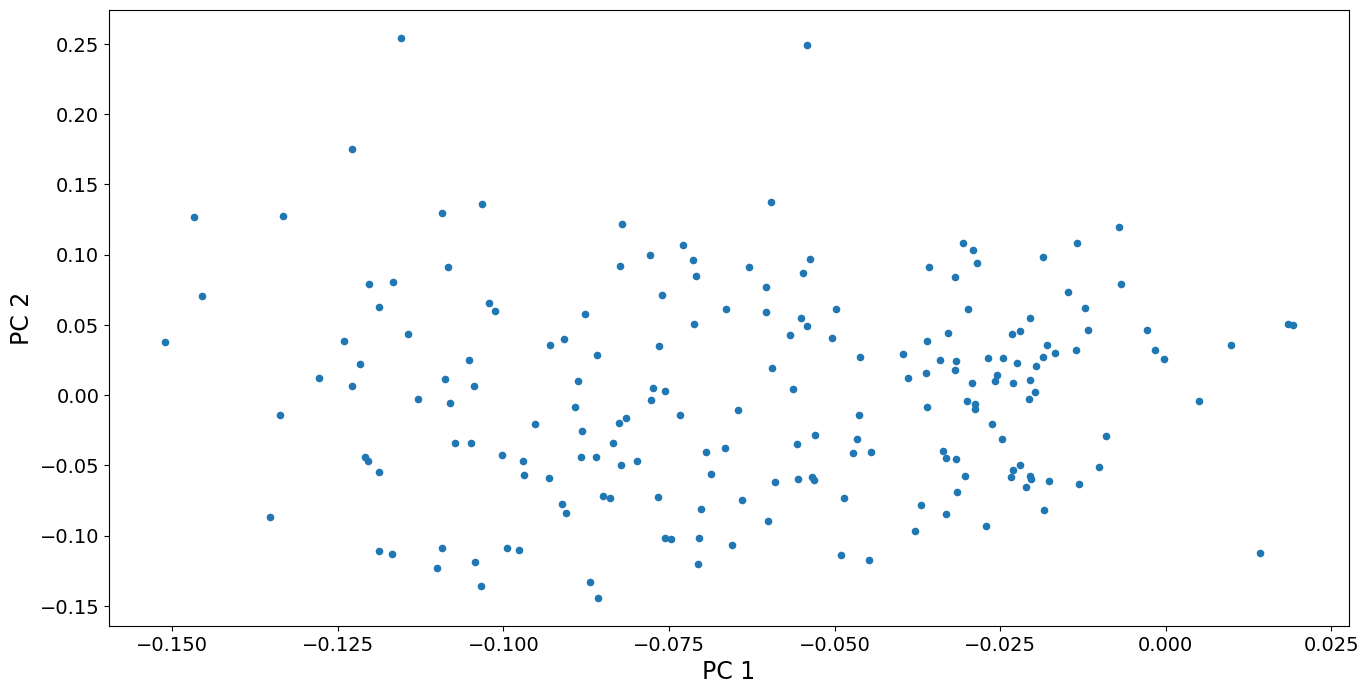
最初の2つの主成分スコアの散布図を見ることもできます。PC2で最も高いスコアを持つ2つの国は、他の点からやや離れていることを除けば、国々の変化は比較的連続していることがわかります。これらの国、オマーンとイエメンは、1980年頃に出生率が急増したという点で独特です。他のどの国にもそのような急増はありません。対照的に、PC1で高いスコアを持つ国(出生率が継続的に増加している国)は、変化の連続体の一部です。
[13]:
fig, ax = plt.subplots()
pca_model.loadings.plot.scatter(x="comp_00", y="comp_01", ax=ax)
ax.set_xlabel("PC 1", size=17)
ax.set_ylabel("PC 2", size=17)
dta.index[pca_model.loadings.iloc[:, 1] > 0.2].values
[13]:
array(['Oman', 'Yemen, Rep.'], dtype=object)