状態空間モデル - チャンドラセカール漸化式

[1]:

%matplotlib inline

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

from pandas_datareader.data import DataReader

状態空間モデルに関するほとんどの演算はカルマンフィルタ漸化式に依存していますが、いくつかの特別なケースでは、「チャンドラセカール漸化式」と呼ばれる別々の方法を使用できます。これらは、状態ベクトルの条件付きモーメントを反復的に計算する代替手段を提供し、場合によっては、カルマンフィルタ漸化式よりも計算コストが大幅に低減される可能性があります。詳細については、「DSGEモデルの尤度評価における「チャンドラセカール漸化式」の利用」(Herbst, 2015)を参照してください。ここでは、基本的なアイデアの概要を説明します。

状態空間モデルとカルマンフィルタ

時間不変の状態空間モデルは、次のように記述できることを思い出してください。

\[\begin{split}\begin{aligned} y_t &= Z \alpha_t + \varepsilon_t, \qquad \varepsilon_t \sim N(0, H) \\ \alpha_{t+1} & = T \alpha_t + R \eta_t, \qquad \eta_t \sim N(0, Q) \\ \alpha_1 & \sim N(a_1, P_1) \end{aligned}\end{split}\]

ここで、\(y_t\)は\(p \times 1\)ベクトルであり、\(\alpha_t\)は\(m \times 1\)ベクトルです。

カルマンフィルタの各反復（例えば、時刻\(t\)）は、3つの部分に分割できます。

  1. **初期化**: 条件付き状態分布\(\alpha_t \mid y^{t-1} \sim N(a_t, P_t)\)を定義する\(a_t\)と\(P_t\)の指定。

  2. **更新**: 条件付き状態分布\(\alpha_t \mid y^{t} \sim N(a_{t|t}, P_{t|t})\)を定義する\(a_{t|t}\)と\(P_{t|t}\)の計算。

  3. **予測**: 条件付き状態分布\(\alpha_{t+1} \mid y^{t} \sim N(a_{t+1}, P_{t+1})\)を定義する\(a_{t+1}\)と\(P_{t+1}\)の計算。

もちろん、最初の反復の後、予測部分は次のステップの初期化に必要な値を提供します。

予測ステップに焦点を当てると、カルマンフィルタ漸化式は次のようになります。

\[\begin{split}\begin{aligned} a_{t+1} & = T a_{t|t} \\ P_{t+1} & = T P_{t|t} T' + R Q R' \\ \end{aligned}\end{split}\]

ここで、行列\(T\)と\(P_{t|t}\)はそれぞれ\(m \times m\)であり、\(m\)は状態ベクトル\(\alpha\)のサイズです。場合によっては、状態ベクトルが非常に大きくなり、\(P_{t+1}\)を生成するために必要な行列乗算が計算集約的になる可能性があります。

例：季節自己回帰

例として、AR(r)モデル（観測ベクトルの次元として\(p\)を既に使用しているため、ここでは\(r\)を使用します）は、次のように状態空間形式で表すことができます。

\[\begin{split}\begin{aligned} y_t &= \alpha_t \\ \alpha_{t+1} & = T \alpha_t + R \eta_t, \qquad \eta_t \sim N(0, Q) \end{aligned}\end{split}\]

ここで

\[\begin{split}\begin{aligned} T = \begin{bmatrix} \phi_1 & \phi_2 & \dots & \phi_r \\ 1 & 0 & & 0 \\ \vdots & \ddots & & \vdots \\ 0 & & 1 & 0 \\ \end{bmatrix} \qquad R = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} \qquad Q = \begin{bmatrix} \sigma^2 \end{bmatrix} \end{aligned}\end{split}\]

日次データで年間季節性を示すARモデルでは、最大\(r=365\)までのラグを組み込んだモデルを適合させたい場合があります。この場合、状態ベクトルは少なくとも\(m = 365\)になります。\(T\)と\(P_{t|t}\)の行列はそれぞれ\(365^2 = 133225\)個の要素を持つため、尤度関数の計算（カルマンフィルタを使用）に費やされる時間のほとんどは、予測ステップでの行列乗算によって支配される可能性があります。

状態空間モデルとチャンドラセカール漸化式

チャンドラセカール漸化式は、式\(P_{t+1} = T P_{t|t} T' + R Q R'\)を異なる漸化式で置き換えます。

\[P_{t+1} = P_t + W_t M_t W_t'\]

ただし、\(W_t\)は\(m \times p\)次元の行列であり、\(M_t\)は\(p \times p\)次元の行列であり、\(p\)は観測ベクトル\(y_t\)の次元です。これらの行列自体も再帰的な定式化を持っています。\(W_t\)と\(M_t\)を計算するための式の詳細については、Herbst (2015)を参照してください。

**重要な注意**: カルマンフィルタとは異なり、チャンドラセカール漸化式はすべての状態空間モデルで使用できるわけではありません。特に、後者は次の制限があります（前者の使用には必要ありません）。

  • モデルは時間不変でなければなりません。ただし、時間変動する切片は許可されます。

  • 状態ベクトルの定常的な初期化を使用する必要があります（非定常成分のすべてのモデルを除外します）。

  • 欠損データは許可されません。

この式がより効率的な計算を意味する理由を理解するために、上記のSARIMAXのケースをもう一度考えてみましょう。この場合、\(p = 1\)なので、\(M_t\)はスカラーであり、チャンドラセカール漸化式を次のように書き直すことができます。

\[P_{t+1} = P_t + M_t \times W_t W_t'\]

乗算される行列\(W_t\)は、\(m \times 1\)次元であり、\(r=365\)の場合、それぞれ\(365^2\)個ではなく\(365\)個の要素しかありません。これは、予測ステップを完了するために必要な計算が大幅に減少することを意味します。

収束

パフォーマンスへの影響に関する簡単な議論を複雑にする要因は、時間不変モデルでは、予測された状態共分散行列が一定の行列に収束するというよく知られた事実です。これは、すべての\(t > S\)に対して\(P_t = P_{t+1}\)となるような\(S\)が存在することを意味します。収束が達成されると、予測ステップから\(P_{t+1}\)の式を完全に削除できます。

AR(r)モデルのような単純な時系列モデルでは、収束は比較的速く達成され、これにより、チャンドラセカール漸化式を使用することによるパフォーマンス上の利点が制限される可能性があります。Herbst (2015)は、代わりにDSGE（動学的確率的一般均衡）モデルに焦点を当てています。DSGEモデルは、多くの場合、大きな状態ベクトルと、収束に多くの期間を要することがあります。これらの場合、パフォーマンスの向上は非常に大きくなる可能性があります。

実践例

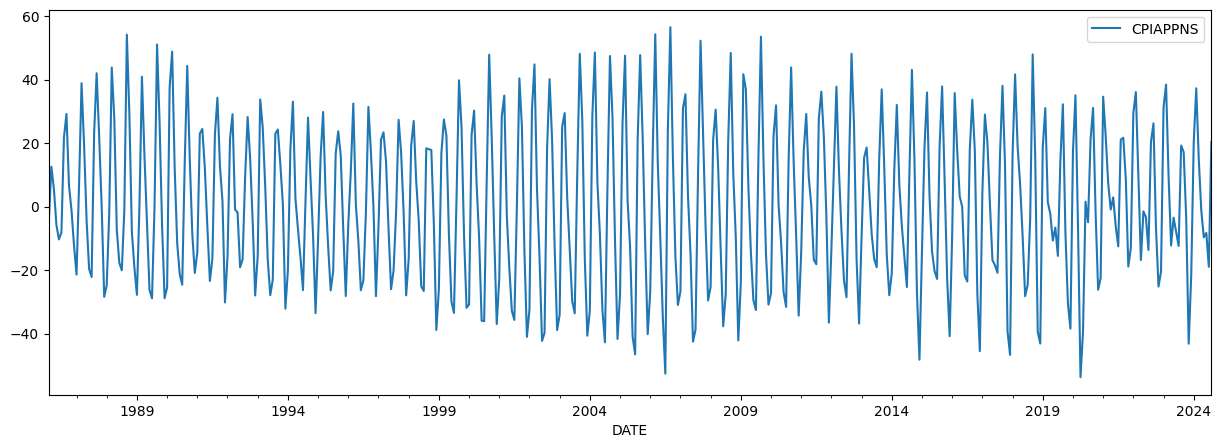
実践例として、明確な季節成分を持つ月次データについて考えます。ここでは、消費者物価指数で測定された衣料品のインフレ率を見ていきます。データのグラフは、強い季節性を示しています。

[2]:

cpi_apparel = DataReader('CPIAPPNS', 'fred', start='1986')
cpi_apparel.index = pd.DatetimeIndex(cpi_apparel.index, freq='MS')
inf_apparel = np.log(cpi_apparel).diff().iloc[1:] * 1200
inf_apparel.plot(figsize=(15, 5));
../../../_images/examples_notebooks_generated_statespace_chandrasekhar_10_0.png

2つのモデルインスタンスを作成します。最初のインスタンスはカルマンフィルタ漸化式を使用するように設定され、2番目のインスタンスはチャンドラセカール漸化式を使用するように設定されます。この設定は、以下に示すようにssm.filter_chandrasekharプロパティによって制御されます。

念頭に置いているモデルは季節自己回帰であり、最初の6か月をラグとして、過去15年間の各月の指定月をラグとして含めます。これは、状態ベクトルが次元\(m = 186\)を持つことを意味し、これはチャンドラセカール漸化式を使用することでかなりのパフォーマンス向上が見られる可能性があるほど十分に大きいです。

**注意**: 各モデルでtolerance=0を設定しています。これは、フィルタが予測共分散行列が収束したことを認識することを防ぐ効果があります。これは実践では推奨されません。ここでは、通常のカルマンフィルタ漸化式ではなく、すべての期間で使用される場合のチャンドラセカール漸化式の優れたパフォーマンスを強調するためにこれを行います。後で、収束を許可するより現実的な設定でのパフォーマンスを示します。

[3]:

# Model that will apply Kalman filter recursions
mod_kf = sm.tsa.SARIMAX(inf_apparel, order=(6, 0, 0), seasonal_order=(15, 0, 0, 12), tolerance=0)
print(mod_kf.k_states)

# Model that will apply Chandrasekhar recursions
mod_ch = sm.tsa.SARIMAX(inf_apparel, order=(6, 0, 0), seasonal_order=(15, 0, 0, 12), tolerance=0)
mod_ch.ssm.filter_chandrasekhar = True

186

以下のコードを使用して、対数尤度関数の計算時間を測定します。

%timeit mod_kf.loglike(mod_kf.start_params)
%timeit mod_ch.loglike(mod_ch.start_params)

これにより、次の結果が得られます。

171 ms ± 19.7 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
85 ms ± 4.97 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

これは、この実験では、チャンドラセカール漸化式によってパフォーマンスが約2倍向上したことを意味します。

前述のように、前の実験では予測共分散行列の収束を無効にしたため、その結果はその上限です。今度は、通常どおりtolerance=0引数を削除することで、収束を許可します。

[4]:

# Model that will apply Kalman filter recursions
mod_kf = sm.tsa.SARIMAX(inf_apparel, order=(6, 0, 0), seasonal_order=(15, 0, 0, 12))
print(mod_kf.k_states)

# Model that will apply Chandrasekhar recursions
mod_ch = sm.tsa.SARIMAX(inf_apparel, order=(6, 0, 0), seasonal_order=(15, 0, 0, 12))
mod_ch.ssm.filter_chandrasekhar = True

186

再度、以下のコードを使用して対数尤度関数の計算時間を計測します。

%timeit mod_kf.loglike(mod_kf.start_params)
%timeit mod_ch.loglike(mod_ch.start_params)

これにより、次の結果が得られます。

114 ms ± 7.64 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
70.5 ms ± 2.43 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

チャンドラセカール漸化式は依然としてパフォーマンスを向上させますが、現在は約33％に過ぎません。その理由は、収束後には予測共分散行列を計算する必要がなくなるため、収束後の期間では、両アプローチ間の計算時間に違いがないためです。以下では、収束が達成された期間を確認します。

[5]:

res_kf = mod_kf.filter(mod_kf.start_params)
print('Convergence at t=%d, of T=%d total observations' %
      (res_kf.filter_results.period_converged, res_kf.nobs))

Convergence at t=186, of T=463 total observations

収束は比較的早い段階で発生したため、既に期間の半分以上でコストの高い行列乗算を回避しています。

しかし、上記のように、より大規模なDSGEモデルでは、サンプルのほとんどまたはすべての期間で収束が達成されない場合があり、そのため、最初の例とより類似したパフォーマンス向上を期待できるかもしれません。McAdamとWarneは、2019年の論文「金融または労働市場の摩擦を伴うユーロ圏の実時間密度予測」において、その適用例において、「標準的なカルマンフィルターと比較して、これらの漸化式は3つのモデルの対数尤度の計算を約50％高速化するという経験があります」と述べています。これは、最初の例で見つけた結果とほぼ同じです。

マルチスレッド行列代数ルーチンに関する補足

上記のタイミングは、Anaconda経由でインストールされたNumpyインストールに基づいており、インテルのMKL BLASおよびLAPACKライブラリを使用しています。これらは、行列代数を高速化するためのマルチスレッド処理を実装しており、ここで扱っているようなより大きな行列の演算に特に役立ちます。これが結果にどのように影響するかを理解するために、このノートブックの最初のセルに以下を追加して、マルチスレッドをオフにすることができます。

import os
os.environ["MKL_NUM_THREADS"] = "1"

これを行うと、最初の例のタイミングは以下のように変わります。

307 ms ± 3.08 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
97.5 ms ± 1.64 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

そして、2番目の例のタイミングは以下のように変わります。

178 ms ± 2.78 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
78.9 ms ± 950 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

どちらも遅くなりますが、典型的なカルマンフィルターの影響ははるかに大きくなります。

これは予想外ではありません。シングルスレッドとマルチスレッドの線形代数間の性能差は、典型的なカルマンフィルターの場合にるかに大きくなります。なぜなら、チャンドラセカール漸化式のポイントは、行列演算のサイズを削減することだからです。つまり、マルチスレッド線形代数が利用できない場合、チャンドラセカール漸化式はさらに大きなパフォーマンス向上をもたらします。

チャンドラセカール漸化式と単変量フィルタリングアプローチ

KoopmanとDurbin（2000）の単変量フィルタリングアプローチとチャンドラセカール漸化式を組み合わせることも可能です。これは、AknoucheとHamdiの2007年の論文「周期的なチャンドラセカール漸化式」の結果を利用することで実現できます。この組み合わせの初期実装はStatsmodelsに含まれています。ただし、実験によると、これは通常のカルマンフィルターと比較してパフォーマンスを低下させる傾向があります。これは、単変量フィルタリング方法について報告されている計算上の節約と一致しており、節約は、状態ベクトルが観測ベクトルに比べて小さい場合に最も大きくなることを示唆しています。

参考文献

Aknouche, Abdelhakim, and Fayçal Hamdi. “Periodic Chandrasekhar recursions.” arXiv preprint arXiv:0711.3857 (2007).

Herbst, Edward. “Using the “Chandrasekhar Recursions” for likelihood evaluation of DSGE models.” Computational Economics 45, no. 4 (2015): 693-705.

Koopman, Siem J., and James Durbin. “Fast filtering and smoothing for multivariate state space models.” Journal of Time Series Analysis 21, no. 3 (2000): 281-296.

McAdam, Peter, and Anders Warne. “Euro area real-time density forecasting with financial or labor market frictions.” International Journal of Forecasting 35, no. 2 (2019): 580-600.

最終更新日：2024年10月3日