生存時間解析手法¶
statsmodels.duration は、打ち切りデータを取り扱うためのいくつかの標準的な手法を実装しています。これらの手法は、データが起点となる時点と、関心のある事象が発生した時点との間の期間からなる場合によく使用されます。典型的な例としては、ある状態と診断された時点を起点とし、関心のある事象が死亡(または疾患の進行、回復など)である医学研究があります。
現在、右打ち切りのみが扱われています。右打ち切りとは、ある時点t以降に事象が発生したことはわかっているが、正確な事象発生時刻がわからない場合に発生します。
生存関数推定と推論¶
statsmodels.api.SurvfuncRight クラスは、右打ち切りされている可能性のあるデータを使用して生存関数を推定するために使用できます。SurvfuncRight は、生存分布の分位点に関する信頼区間、生存関数に関する点推定と同時信頼帯、プロット手順など、いくつかの推論手順を実装しています。duration.survdiff 関数は、生存分布を比較するための検定手順を提供します。
ここでは、Rのデータセットリポジトリから入手できるflchain研究のデータを使用してSurvfuncRightオブジェクトを作成します。女性被験者のみについて生存分布を適合させます。
In [1]: import statsmodels.api as sm
In [2]: data = sm.datasets.get_rdataset("flchain", "survival").data
In [3]: df = data.loc[data.sex == "F", :]
In [4]: sf = sm.SurvfuncRight(df["futime"], df["death"])
summaryメソッドを呼び出すことで、適合された生存分布の主な特徴を確認できます。
In [5]: sf.summary().head()
Out[5]:
Surv prob Surv prob SE num at risk num events
Time
0 0.999310 0.000398 4350 3.0
1 0.998851 0.000514 4347 2.0
2 0.998621 0.000563 4343 1.0
3 0.997931 0.000689 4342 3.0
4 0.997471 0.000762 4338 2.0
生存分布の分位点に関する点推定値と信頼区間を取得できます。この研究では被験者の約30%のみが死亡したため、0.3確率点以下の分位点しか推定できません。
In [6]: sf.quantile(0.25)
Out[6]: np.int64(3995)
In [7]: sf.quantile_ci(0.25)
Out[7]: (np.int64(3776), np.int64(4166))
単一の生存関数をプロットするには、plotメソッドを呼び出します。
In [8]: sf.plot()
Out[8]: <Figure size 640x480 with 1 Axes>
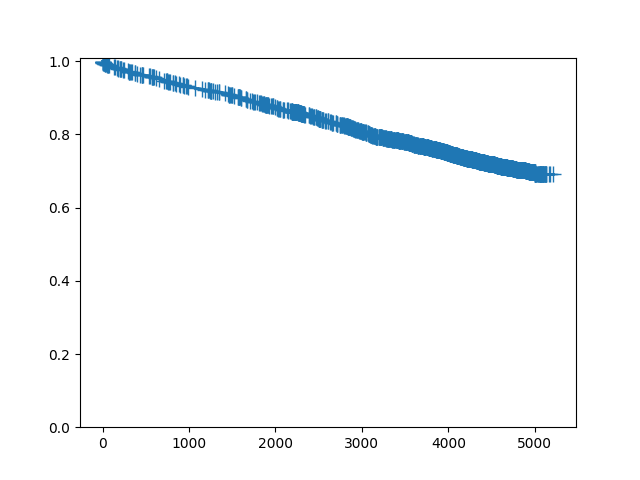
これは打ち切りの多い大規模なデータセットであるため、打ち切り記号をプロットしない方がよい場合があります。
In [9]: fig = sf.plot()
In [10]: ax = fig.get_axes()[0]
In [11]: pt = ax.get_lines()[1]
In [12]: pt.set_visible(False)
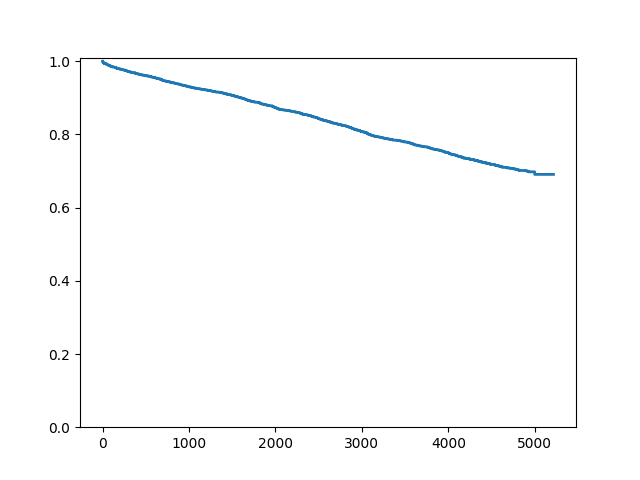
プロットに95%の同時信頼帯を追加することもできます。通常、これらの帯は分布の中央部分のみにプロットされます。
In [13]: fig = sf.plot()
In [14]: lcb, ucb = sf.simultaneous_cb()
In [15]: ax = fig.get_axes()[0]
In [16]: ax.fill_between(sf.surv_times, lcb, ucb, color='lightgrey')
Out[16]: <matplotlib.collections.PolyCollection at 0x7f19af039cf0>
In [17]: ax.set_xlim(365, 365*10)
Out[17]: (365.0, 3650.0)
In [18]: ax.set_ylim(0.7, 1)
Out[18]: (0.7, 1.0)
In [19]: ax.set_ylabel("Proportion alive")
Out[19]: Text(0, 0.5, 'Proportion alive')
In [20]: ax.set_xlabel("Days since enrollment")
Out[20]: Text(0.5, 0, 'Days since enrollment')
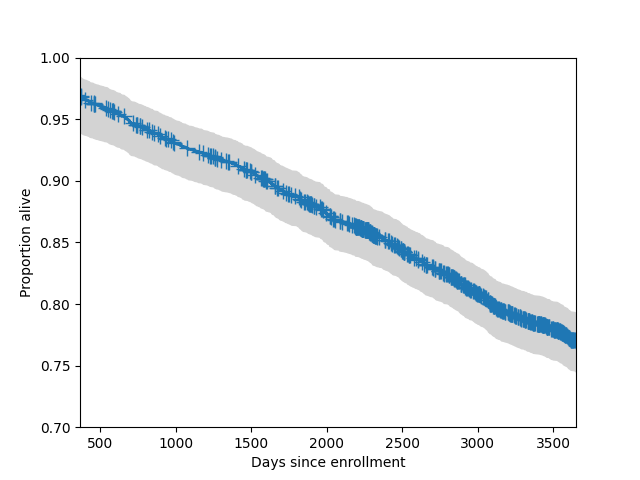
ここでは、2つのグループ(女性と男性)の生存関数を同じ軸上にプロットします。
In [21]: import matplotlib.pyplot as plt
In [22]: gb = data.groupby("sex")
In [23]: ax = plt.axes()
In [24]: sexes = []
In [25]: for g in gb:
....: sexes.append(g[0])
....: sf = sm.SurvfuncRight(g[1]["futime"], g[1]["death"])
....: sf.plot(ax)
....:
In [26]: li = ax.get_lines()
In [27]: li[1].set_visible(False)
In [28]: li[3].set_visible(False)
In [29]: plt.figlegend((li[0], li[2]), sexes, loc="center right")
Out[29]: <matplotlib.legend.Legend at 0x7f19aef908b0>
In [30]: plt.ylim(0.6, 1)
Out[30]: (0.6, 1.0)
In [31]: ax.set_ylabel("Proportion alive")
Out[31]: Text(0, 0.5, 'Proportion alive')
In [32]: ax.set_xlabel("Days since enrollment")
Out[32]: Text(0.5, 0, 'Days since enrollment')
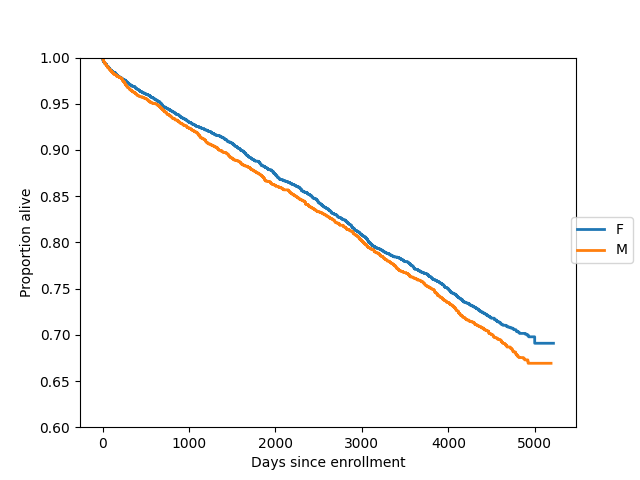
いくつかの標準的なノンパラメトリック手順を実装しているsurvdiffを使用して、2つの生存分布を正式に比較できます。デフォルトの手順はログランク検定です。
In [33]: stat, pv = sm.duration.survdiff(data.futime, data.death, data.sex)
survdiffで実装されている他の検定手順の一部を次に示します。
# Fleming-Harrington with p=1, i.e. weight by pooled survival time
In [34]: stat, pv = sm.duration.survdiff(data.futime, data.death, data.sex, weight_type='fh', fh_p=1)
# Gehan-Breslow, weight by number at risk
In [35]: stat, pv = sm.duration.survdiff(data.futime, data.death, data.sex, weight_type='gb')
# Tarone-Ware, weight by the square root of the number at risk
In [36]: stat, pv = sm.duration.survdiff(data.futime, data.death, data.sex, weight_type='tw')
回帰手法¶
比例ハザード回帰モデル(「Coxモデル」)は、打ち切りデータに対する回帰手法です。線形回帰モデルや一般化線形回帰モデルと同様に、事象までの時間の変化を共変量で説明できます。これらのモデルは、「ハザード比」という形で共変量の作用を表し、ハザード(瞬間的な事象発生率)は共変量の値に応じて特定の係数で乗算されます。
In [37]: import statsmodels.api as sm
In [38]: import statsmodels.formula.api as smf
In [39]: data = sm.datasets.get_rdataset("flchain", "survival").data
In [40]: del data["chapter"]
In [41]: data = data.dropna()
In [42]: data["lam"] = data["lambda"]
In [43]: data["female"] = (data["sex"] == "F").astype(int)
In [44]: data["year"] = data["sample.yr"] - min(data["sample.yr"])
In [45]: status = data["death"].values
In [46]: mod = smf.phreg("futime ~ 0 + age + female + creatinine + np.sqrt(kappa) + np.sqrt(lam) + year + mgus", data, status=status, ties="efron")
In [47]: rslt = mod.fit()
In [48]: print(rslt.summary())
Results: PHReg
====================================================================
Model: PH Reg Sample size: 6524
Dependent variable: futime Num. events: 1962
Ties: Efron
--------------------------------------------------------------------
log HR log HR SE HR t P>|t| [0.025 0.975]
--------------------------------------------------------------------
age 0.1012 0.0025 1.1065 40.9289 0.0000 1.1012 1.1119
female -0.2817 0.0474 0.7545 -5.9368 0.0000 0.6875 0.8280
creatinine 0.0134 0.0411 1.0135 0.3271 0.7436 0.9351 1.0985
np.sqrt(kappa) 0.4047 0.1147 1.4988 3.5288 0.0004 1.1971 1.8766
np.sqrt(lam) 0.7046 0.1117 2.0230 6.3056 0.0000 1.6251 2.5183
year 0.0477 0.0192 1.0489 2.4902 0.0128 1.0102 1.0890
mgus 0.3160 0.2532 1.3717 1.2479 0.2121 0.8350 2.2532
====================================================================
Confidence intervals are for the hazard ratios
詳細な例については、例を参照してください。
Wikiには、いくつかのノートブックの例があります。 PHRegと生存分析のWikiノートブック
参考文献¶
Cox比例ハザード回帰モデルの参考文献
T Therneau (1996). Extending the Cox model. Technical report.
http://www.mayo.edu/research/documents/biostat-58pdf/DOC-10027288
G Rodriguez (2005). Non-parametric estimation in survival models.
http://data.princeton.edu/pop509/NonParametricSurvival.pdf
B Gillespie (2006). Checking the assumptions in the Cox proportional
hazards model.
http://www.mwsug.org/proceedings/2006/stats/MWSUG-2006-SD08.pdf
モジュールリファレンス¶
生存分布を扱うためのクラスは次のとおりです。
|
生存関数の推定と推論。 |
比例ハザード回帰モデルのクラスは次のとおりです。
|
Cox比例ハザード回帰モデル |
比例ハザード回帰の結果クラスは次のとおりです。
|
Cox比例ハザード生存モデルの適合結果を含むクラス。 |
主要なヘルパークラスは次のとおりです。
|
離散分布の集合を表すクラス。 |