コピュラ - 多変量同時分布¶

[1]:

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from scipy import stats

sns.set_style("darkgrid")
sns.mpl.rc("figure", figsize=(8, 8))

[2]:

%%javascript
IPython.OutputArea.prototype._should_scroll = function(lines) {
    return false;
}

システムをモデル化する際、複数のパラメータが関与する場合がよくあります。これらのパラメータはそれぞれ、特定の確率密度関数（PDF）で記述できます。パラメータ値の新しいセットを生成できるようにするには、これらの分布（周辺分布とも呼ばれます）からサンプリングできる必要があります。主に2つの場合があります。（i） PDFが独立している場合。（ii） 依存関係がある場合。依存関係をモデル化する方法の1つは、コピュラを使用することです。

コピュラからのサンプリング¶

2変量の例を使用して、最初に事前分布があり、2つの変数の間の依存関係をモデル化する方法を知っていると仮定しましょう。

この場合、ガンベルコピュラを使用し、そのハイパーパラメータtheta=2を固定します。その2次元PDFを視覚化できます。

[3]:

from statsmodels.distributions.copula.api import (
    CopulaDistribution, GumbelCopula, IndependenceCopula)

copula = GumbelCopula(theta=2)
_ = copula.plot_pdf()  # returns a matplotlib figure

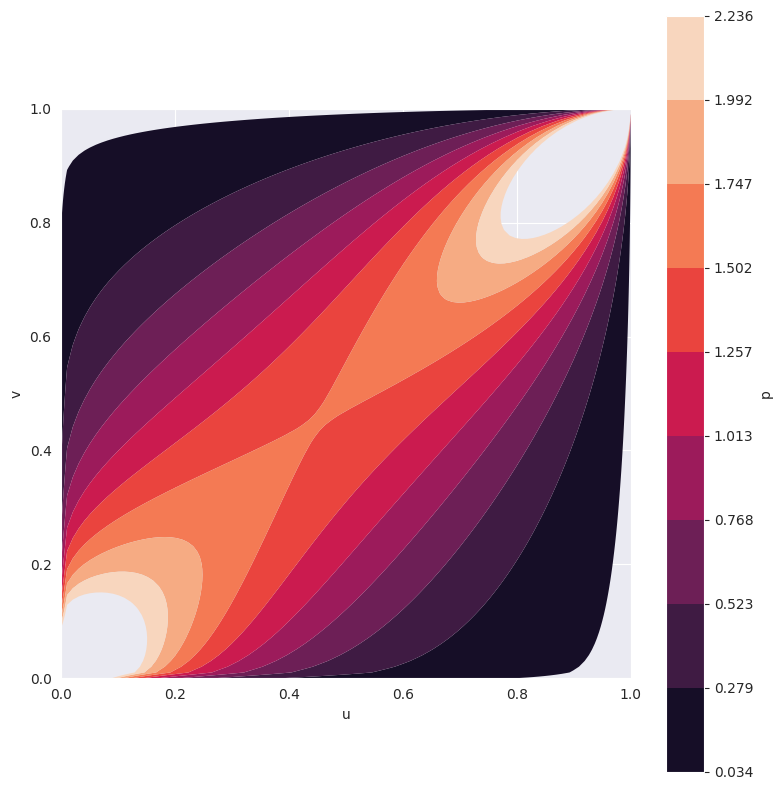
そして、PDFをサンプリングできます。

[4]:

sample = copula.rvs(10000)
h = sns.jointplot(x=sample[:, 0], y=sample[:, 1], kind="hex")
_ = h.set_axis_labels("X1", "X2", fontsize=16)

/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tools/rng_qrng.py:54: FutureWarning: Passing `None` as the seed currently return the NumPy singleton RandomState
(np.random.mtrand._rand). After release 0.13 this will change to using the
default generator provided by NumPy (np.random.default_rng()). If you need
reproducible draws, you should pass a seeded np.random.Generator, e.g.,

import numpy as np
seed = 32839283923801
rng = np.random.default_rng(seed)"

  warnings.warn(_future_warn, FutureWarning)

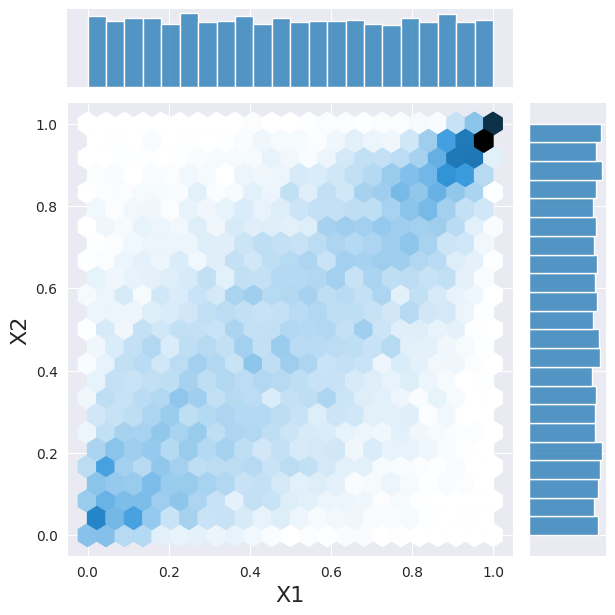
少しの間、2つの変数に戻りましょう。この場合、それらはガンマ分布と正規分布に従うと見なします。互いに独立している場合、各PDFから個別にサンプリングできます。ここでは、便利なクラスを使用して同じ操作を実行します。

再現性¶

コピュラから再現可能な乱数を生成するには、明示的に`seed`引数を設定する必要があります。 `seed`は、初期化されたNumPyの`Generator`または`RandomState`、あるいは`np.random.default_rng`に許容される引数（整数または整数のシーケンスなど）を受け入れます。この例では整数を使用しています。

`np.random`ディストリビューションで直接公開されているシングルトン`RandomState`は使用されず、`np.random.seed`を設定しても生成される値には影響しません。

[5]:

marginals = [stats.gamma(2), stats.norm]
joint_dist = CopulaDistribution(copula=IndependenceCopula(), marginals=marginals)
sample = joint_dist.rvs(512, random_state=20210801)
h = sns.jointplot(x=sample[:, 0], y=sample[:, 1], kind="scatter")
_ = h.set_axis_labels("X1", "X2", fontsize=16)

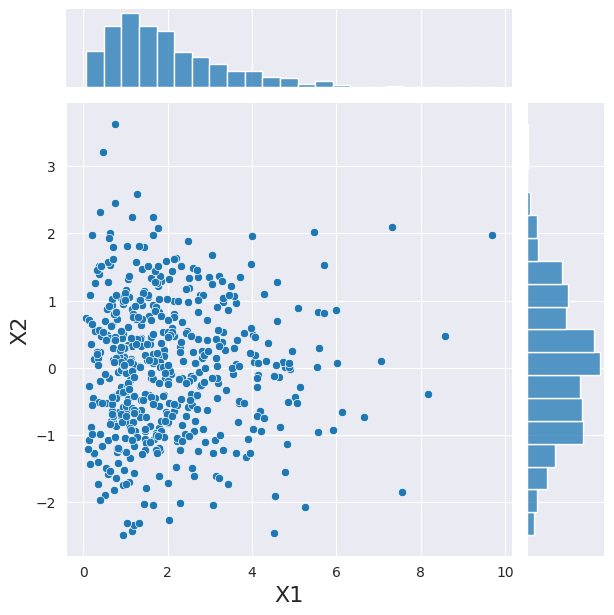
さて、上記ではコピュラを使用して変数間の依存関係を表現しました。このコピュラを使用して、同じ便利なクラスで新しい観測値セットをサンプリングできます。

[6]:

joint_dist = CopulaDistribution(copula, marginals)
# Use an initialized Generator object
rng = np.random.default_rng([2, 0, 2, 1, 0, 8, 0, 1])
sample = joint_dist.rvs(512, random_state=rng)
h = sns.jointplot(x=sample[:, 0], y=sample[:, 1], kind="scatter")
_ = h.set_axis_labels("X1", "X2", fontsize=16)

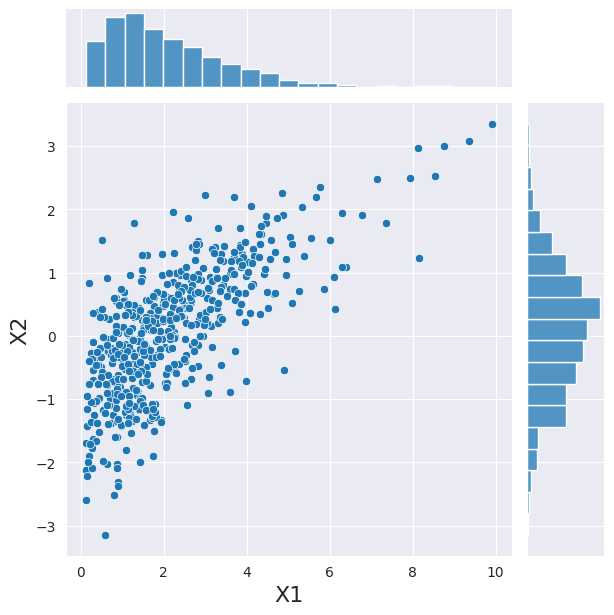
ここで注意すべき点が2つあります。（i） 独立の場合と同様に、周辺分布はガンマ分布と正規分布を正しく示しています。（ii） 2つの変数の間に依存関係が見られます。

コピュラパラメータの推定¶

さて、既に実験データがあり、ガンベルコピュラを使用して表現できる依存関係があるとします。しかし、コピュラのハイパーパラメータ値がわかりません。この場合、値を推定できます。

取得するはずのハイパーパラメータの値（theta=2）を既に知っているため、先ほど生成したサンプルを使用します。

[7]:

copula = GumbelCopula()
theta = copula.fit_corr_param(sample)
print(theta)

2.049379621506455

推定されたハイパーパラメータ値は、以前に設定した値に近いことがわかります。