自己回帰¶
このノートブックでは、`AutoReg` モデルを用いた自己回帰モデリングを紹介します。また、AICなどの情報量基準を最小化するモデルの選択を支援する `ar_select_order` についても説明します。自己回帰モデルは、以下の式で表されるダイナミクスを持ちます。
`AutoReg` は、以下のモデルも許可します。
決定論的項 (`trend`)
`n`: 決定論的項なし
`c`: 定数 (デフォルト)
`ct`: 定数と時間トレンド
`t`: 時間トレンドのみ
季節ダミー (`seasonal`)
`True` は、時系列の周期を \(s\) (例えば、月次データの場合は12) とすると、\(s-1\) 個のダミー変数を含めます。
カスタム決定論的項 (`deterministic`)
`DeterministicProcess` を受け入れます。
外生変数 (`exog`)
モデルに含める外生変数の `DataFrame` または `array` です。
選択されたラグの省略 (`lags`)
`lags` が整数の反復可能なオブジェクトの場合、これらのラグのみがモデルに含まれます。
完全な仕様は以下のとおりです。
ここで、
\(d_i\) は、\(mod(t, period) = i\) の場合に 1 となる季節ダミー変数です。モデルに定数が含まれている場合 ( `trend` に `c` が含まれている場合)、周期 0 は除外されます。
\(t\) は、最初の観測値で 1 から始まる時間トレンド (\(1,2,\ldots\)) です。
\(x_{t,j}\) は外生回帰変数です。**注** これらは、モデルを定義する際に左辺の変数と時間的に整合されます。
\(\epsilon_t\) は、ホワイトノイズプロセスであると仮定されます。
最初のセルでは、標準パッケージをインポートし、プロットをインラインで表示するように設定します。
[1]:
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import pandas_datareader as pdr
import seaborn as sns
from statsmodels.tsa.api import acf, graphics, pacf
from statsmodels.tsa.ar_model import AutoReg, ar_select_order
このセルでは、プロットスタイルを設定し、matplotlibのpandas日付コンバーターを登録し、デフォルトの図のサイズを設定します。
[2]:
sns.set_style("darkgrid")
pd.plotting.register_matplotlib_converters()
# Default figure size
sns.mpl.rc("figure", figsize=(16, 6))
sns.mpl.rc("font", size=14)
最初の例では、季節調整されていない米国住宅着工件数の前月比成長率を使用します。季節性は、ピークと谷の規則的なパターンによって明らかです。`AutoReg` を使用したときに警告が発生しないように、時系列の頻度を "MS" (月初め) に設定します。
[3]:
data = pdr.get_data_fred("HOUSTNSA", "1959-01-01", "2019-06-01")
housing = data.HOUSTNSA.pct_change().dropna()
# Scale by 100 to get percentages
housing = 100 * housing.asfreq("MS")
fig, ax = plt.subplots()
ax = housing.plot(ax=ax)
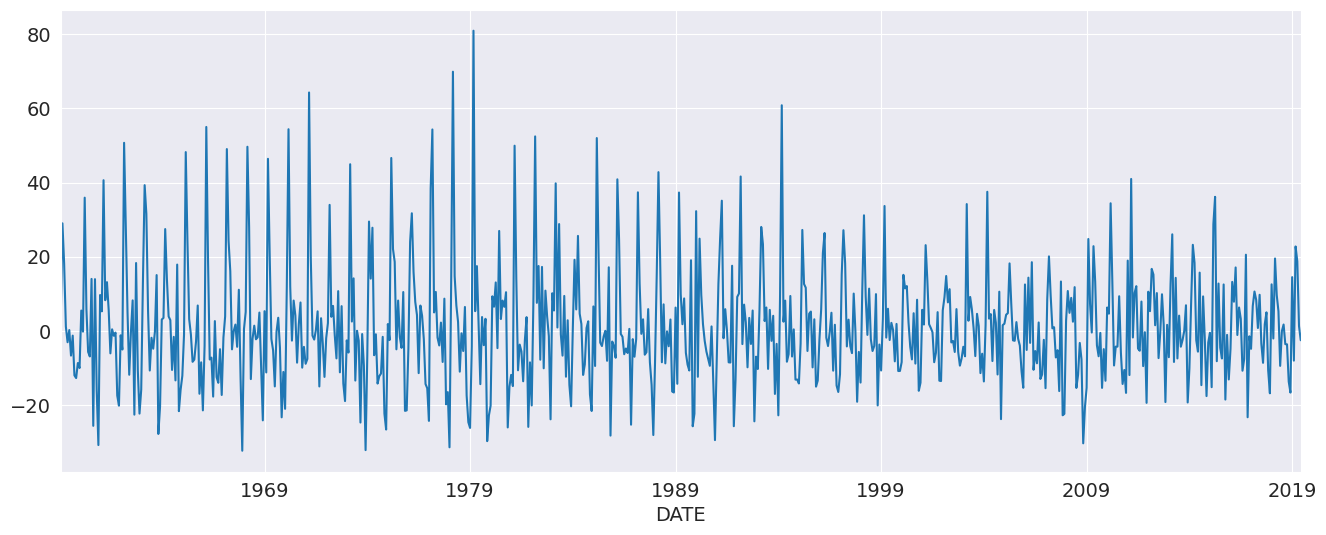
AR(3)から始めることができます。これはこのデータにとって良いモデルではありませんが、APIの基本的な使い方を示しています。
[4]:
mod = AutoReg(housing, 3, old_names=False)
res = mod.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: AutoReg(3) Log Likelihood -2993.442
Method: Conditional MLE S.D. of innovations 15.289
Date: Thu, 03 Oct 2024 AIC 5996.884
Time: 15:55:21 BIC 6019.794
Sample: 05-01-1959 HQIC 6005.727
- 06-01-2019
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 1.1228 0.573 1.961 0.050 0.000 2.245
HOUSTNSA.L1 0.1910 0.036 5.235 0.000 0.120 0.263
HOUSTNSA.L2 0.0058 0.037 0.155 0.877 -0.067 0.079
HOUSTNSA.L3 -0.1939 0.036 -5.319 0.000 -0.265 -0.122
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 0.9680 -1.3298j 1.6448 -0.1499
AR.2 0.9680 +1.3298j 1.6448 0.1499
AR.3 -1.9064 -0.0000j 1.9064 -0.5000
-----------------------------------------------------------------------------
`AutoReg` は、`OLS` と同じ共分散推定量をサポートしています。以下では、Whiteの共分散推定量である `cov_type="HC0"` を使用しています。パラメータ推定値は同じですが、標準誤差に依存するすべての量が変化します。
[5]:
res = mod.fit(cov_type="HC0")
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: AutoReg(3) Log Likelihood -2993.442
Method: Conditional MLE S.D. of innovations 15.289
Date: Thu, 03 Oct 2024 AIC 5996.884
Time: 15:55:21 BIC 6019.794
Sample: 05-01-1959 HQIC 6005.727
- 06-01-2019
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 1.1228 0.601 1.869 0.062 -0.055 2.300
HOUSTNSA.L1 0.1910 0.035 5.499 0.000 0.123 0.259
HOUSTNSA.L2 0.0058 0.039 0.150 0.881 -0.070 0.081
HOUSTNSA.L3 -0.1939 0.036 -5.448 0.000 -0.264 -0.124
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 0.9680 -1.3298j 1.6448 -0.1499
AR.2 0.9680 +1.3298j 1.6448 0.1499
AR.3 -1.9064 -0.0000j 1.9064 -0.5000
-----------------------------------------------------------------------------
[6]:
sel = ar_select_order(housing, 13, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: AutoReg(13) Log Likelihood -2676.157
Method: Conditional MLE S.D. of innovations 10.378
Date: Thu, 03 Oct 2024 AIC 5382.314
Time: 15:55:21 BIC 5450.835
Sample: 03-01-1960 HQIC 5408.781
- 06-01-2019
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
const 1.3615 0.458 2.970 0.003 0.463 2.260
HOUSTNSA.L1 -0.2900 0.036 -8.161 0.000 -0.360 -0.220
HOUSTNSA.L2 -0.0828 0.031 -2.652 0.008 -0.144 -0.022
HOUSTNSA.L3 -0.0654 0.031 -2.106 0.035 -0.126 -0.005
HOUSTNSA.L4 -0.1596 0.031 -5.166 0.000 -0.220 -0.099
HOUSTNSA.L5 -0.0434 0.031 -1.387 0.165 -0.105 0.018
HOUSTNSA.L6 -0.0884 0.031 -2.867 0.004 -0.149 -0.028
HOUSTNSA.L7 -0.0556 0.031 -1.797 0.072 -0.116 0.005
HOUSTNSA.L8 -0.1482 0.031 -4.803 0.000 -0.209 -0.088
HOUSTNSA.L9 -0.0926 0.031 -2.960 0.003 -0.154 -0.031
HOUSTNSA.L10 -0.1133 0.031 -3.665 0.000 -0.174 -0.053
HOUSTNSA.L11 0.1151 0.031 3.699 0.000 0.054 0.176
HOUSTNSA.L12 0.5352 0.031 17.133 0.000 0.474 0.596
HOUSTNSA.L13 0.3178 0.036 8.937 0.000 0.248 0.388
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 1.0913 -0.0000j 1.0913 -0.0000
AR.2 0.8743 -0.5018j 1.0080 -0.0829
AR.3 0.8743 +0.5018j 1.0080 0.0829
AR.4 0.5041 -0.8765j 1.0111 -0.1669
AR.5 0.5041 +0.8765j 1.0111 0.1669
AR.6 0.0056 -1.0530j 1.0530 -0.2491
AR.7 0.0056 +1.0530j 1.0530 0.2491
AR.8 -0.5263 -0.9335j 1.0716 -0.3317
AR.9 -0.5263 +0.9335j 1.0716 0.3317
AR.10 -0.9525 -0.5880j 1.1194 -0.4120
AR.11 -0.9525 +0.5880j 1.1194 0.4120
AR.12 -1.2928 -0.2608j 1.3189 -0.4683
AR.13 -1.2928 +0.2608j 1.3189 0.4683
------------------------------------------------------------------------------
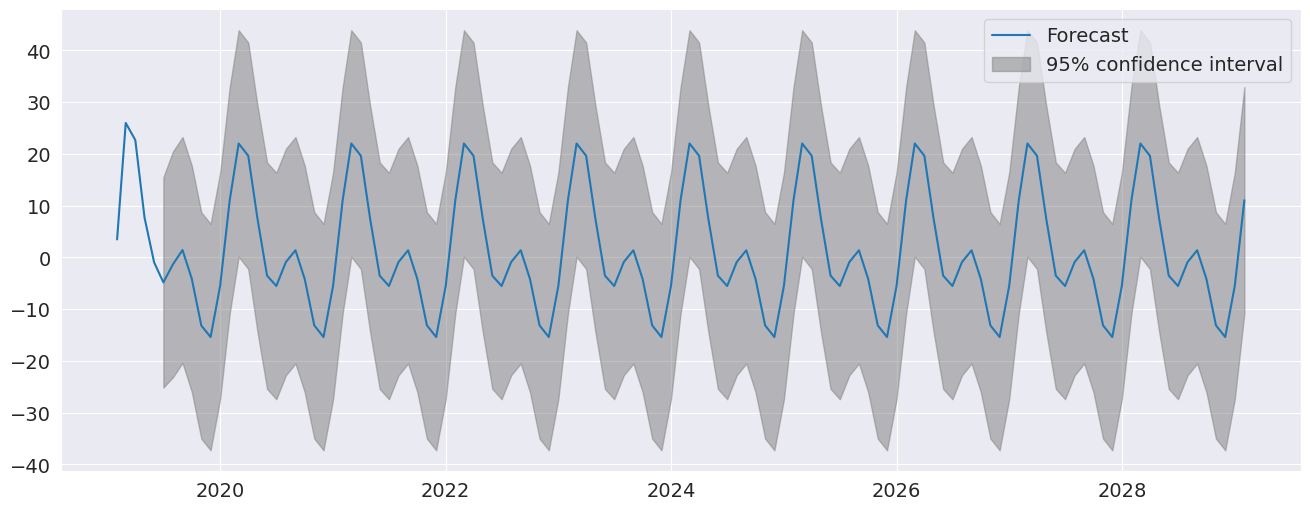
`plot_predict` は予測を可視化します。ここでは、モデルによって捉えられた強い季節性を示す多数の予測を生成します。
[7]:
fig = res.plot_predict(720, 840)
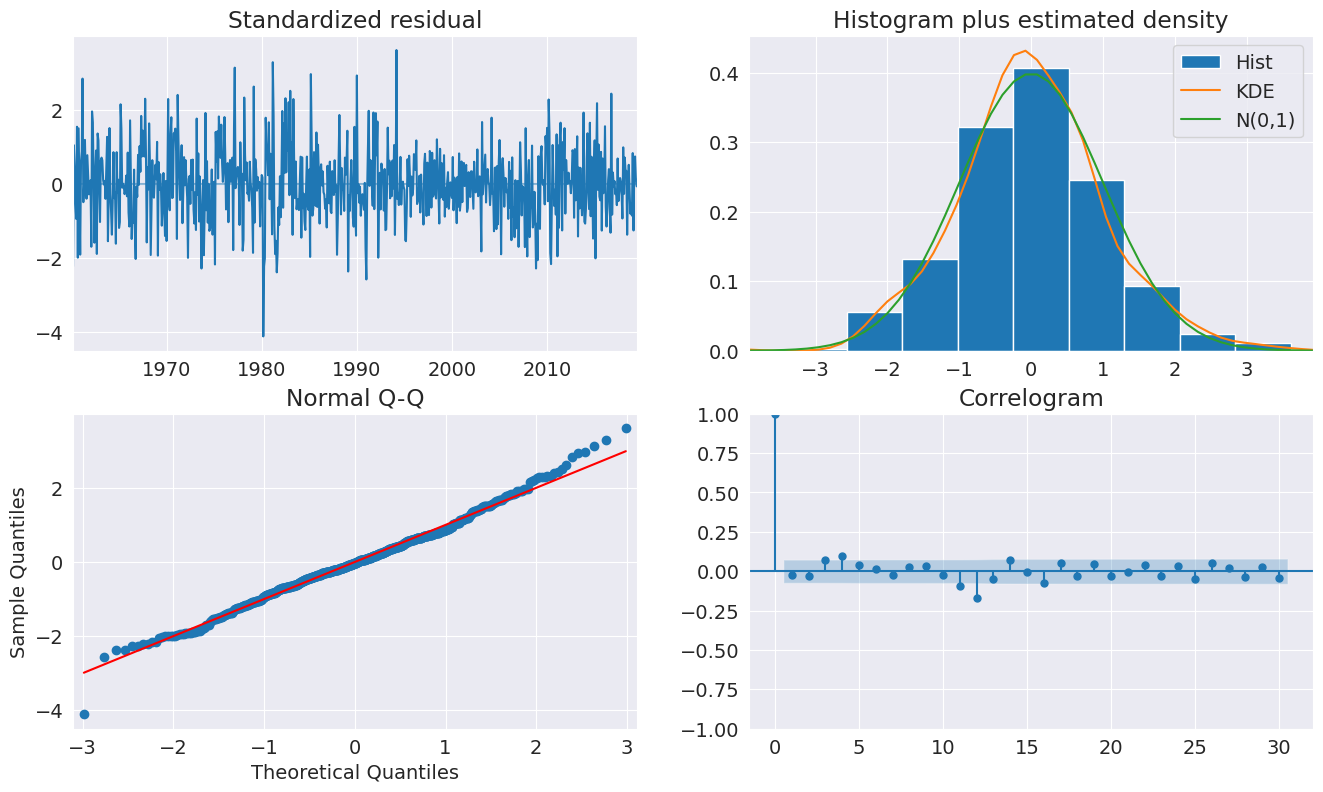
`plot_diagnositcs` は、モデルがデータの主要な特徴を捉えていることを示しています。
[8]:
fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(fig=fig, lags=30)
季節ダミー¶
`AutoReg` は、季節性をモデル化する別の方法である季節ダミーをサポートしています。ダミー変数を含めると、ダイナミクスはAR(2)に短縮されます。
[9]:
sel = ar_select_order(housing, 13, seasonal=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: Seas. AutoReg(2) Log Likelihood -2652.556
Method: Conditional MLE S.D. of innovations 9.487
Date: Thu, 03 Oct 2024 AIC 5335.112
Time: 15:55:27 BIC 5403.863
Sample: 04-01-1959 HQIC 5361.648
- 06-01-2019
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 1.2726 1.373 0.927 0.354 -1.418 3.963
s(2,12) 32.6477 1.824 17.901 0.000 29.073 36.222
s(3,12) 23.0685 2.435 9.472 0.000 18.295 27.842
s(4,12) 10.7267 2.693 3.983 0.000 5.449 16.005
s(5,12) 1.6792 2.100 0.799 0.424 -2.437 5.796
s(6,12) -4.4229 1.896 -2.333 0.020 -8.138 -0.707
s(7,12) -4.2113 1.824 -2.309 0.021 -7.786 -0.636
s(8,12) -6.4124 1.791 -3.581 0.000 -9.922 -2.902
s(9,12) 0.1095 1.800 0.061 0.952 -3.419 3.638
s(10,12) -16.7511 1.814 -9.234 0.000 -20.307 -13.196
s(11,12) -20.7023 1.862 -11.117 0.000 -24.352 -17.053
s(12,12) -11.9554 1.778 -6.724 0.000 -15.440 -8.470
HOUSTNSA.L1 -0.2953 0.037 -7.994 0.000 -0.368 -0.223
HOUSTNSA.L2 -0.1148 0.037 -3.107 0.002 -0.187 -0.042
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -1.2862 -2.6564j 2.9514 -0.3218
AR.2 -1.2862 +2.6564j 2.9514 0.3218
-----------------------------------------------------------------------------
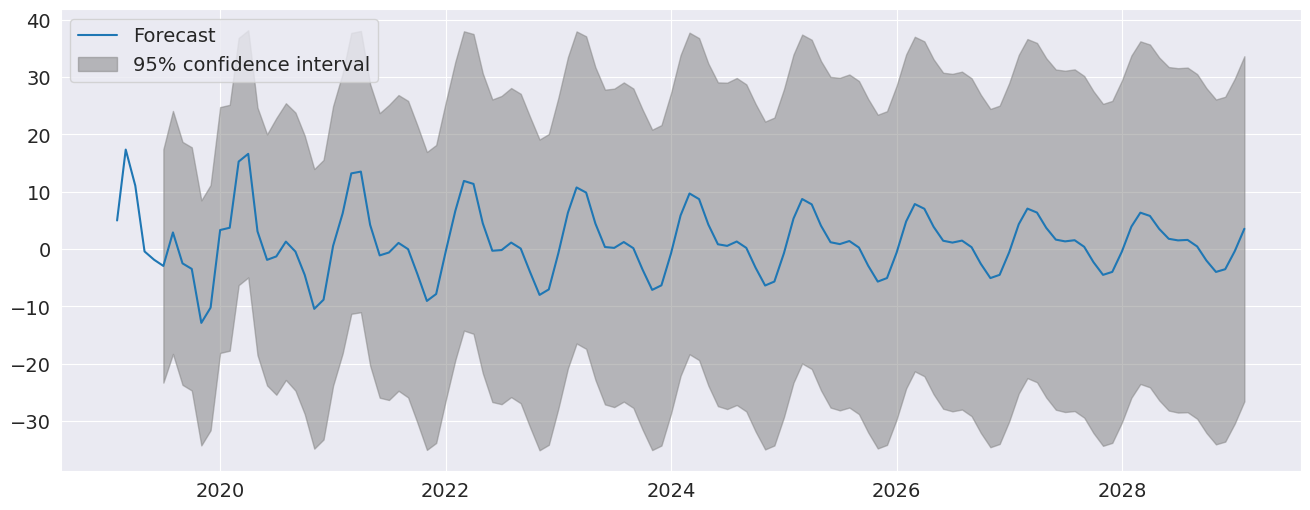
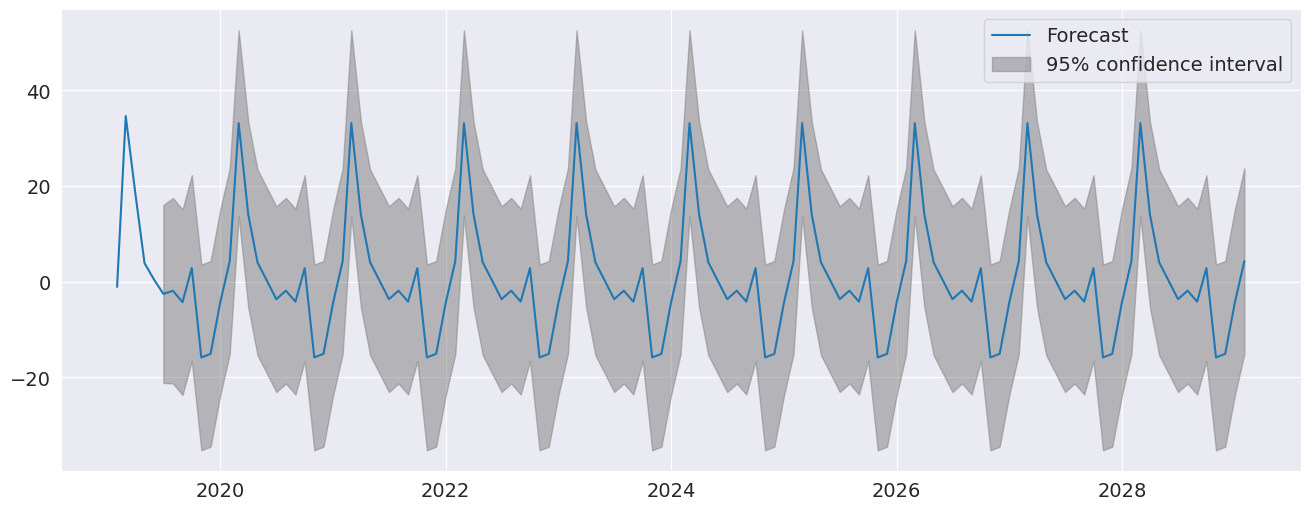
季節ダミーは、10年後までのすべての期間に重要な季節成分を持つ予測において明白です。
[10]:
fig = res.plot_predict(720, 840)
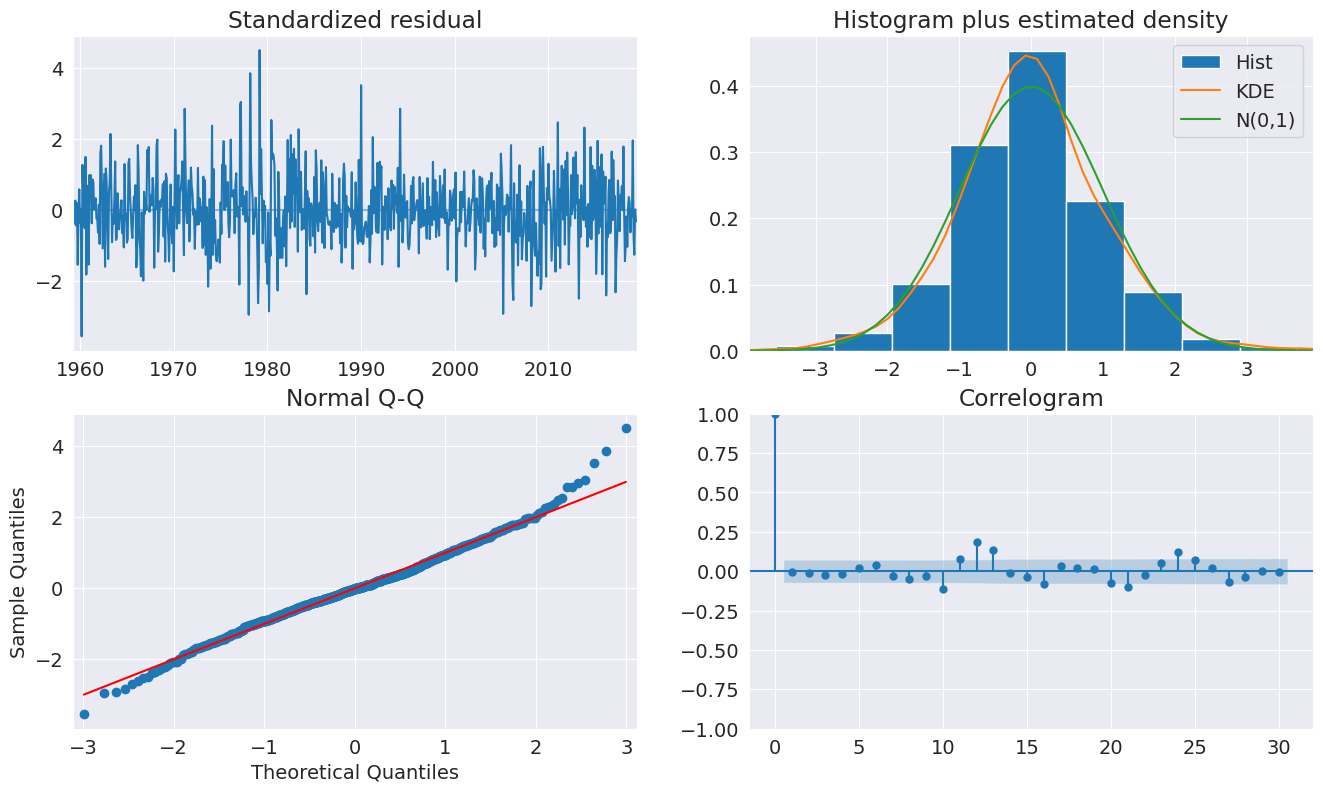
[11]:
fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(lags=30, fig=fig)
季節ダイナミクス¶
`AutoReg` は、OLSを使用してパラメータを推定するため、季節成分を直接サポートしていませんが、季節ARの制約を課さない過剰パラメータ化された季節ARを使用して季節ダイナミクスを捉えることができます。
[12]:
yoy_housing = data.HOUSTNSA.pct_change(12).resample("MS").last().dropna()
_, ax = plt.subplots()
ax = yoy_housing.plot(ax=ax)
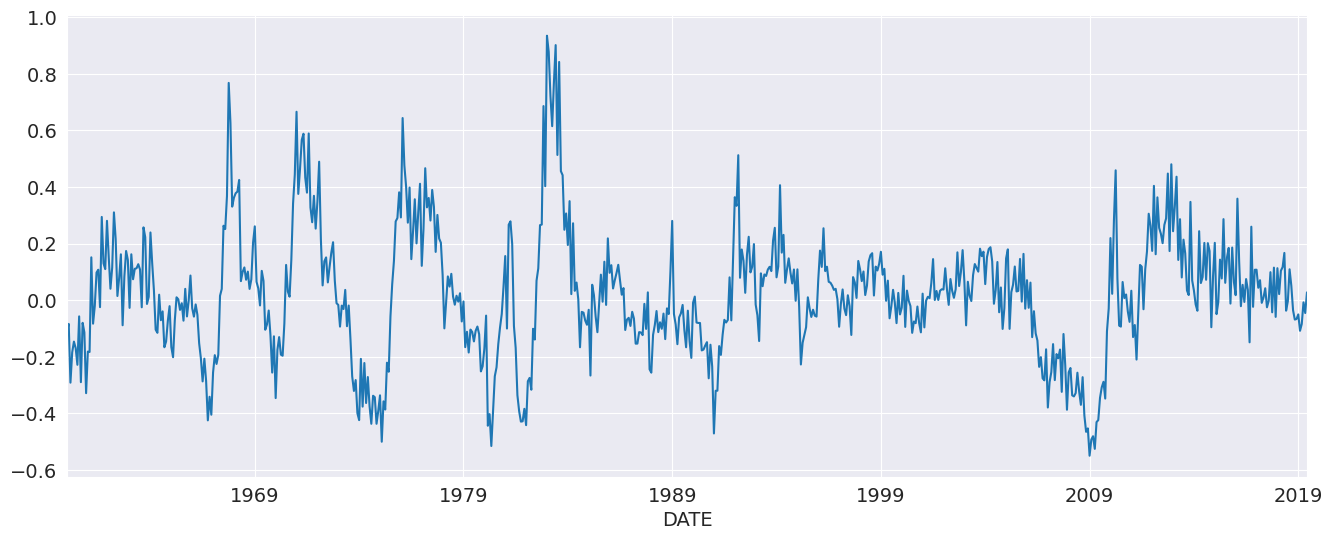
まず、最大ラグのみを選択する単純な方法を使用してモデルを選択します。すべての下位ラグは自動的に含まれます。チェックする最大ラグは13に設定されています。これは、モデルが短期AR(1)成分と季節AR(1)成分の両方を持つ季節ARをネストできるようにするためです。つまり、
展開すると、
となります。`AutoReg` はこの構造を強制しませんが、ネストされたモデル
を推定できます。13個すべてのラグが選択されていることがわかります。
[13]:
sel = ar_select_order(yoy_housing, 13, old_names=False)
sel.ar_lags
[13]:
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]
13個すべてのラグが必要な可能性は低いようです。`glob=True` を設定して、最大13個のラグを含む \(2^{13}\) 個のモデルすべてを検索できます。
ここでは、最初の3つ、7番目、そして最後に12番目と13番目が選択されていることがわかります。これは、表面上は上記で説明した構造と似ています。
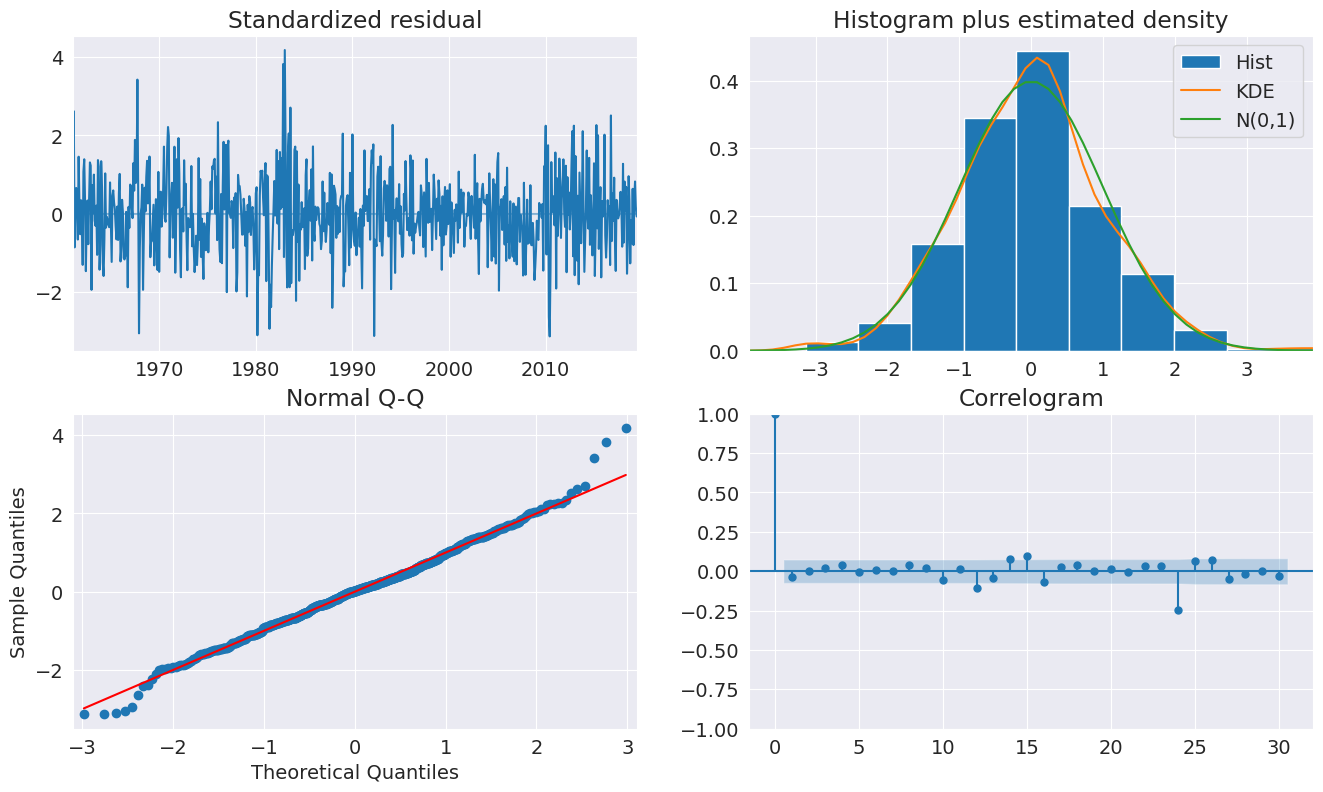
モデルをフィッティングした後、診断プロットを見て、この仕様がデータのダイナミクスを捉えるのに適切であるかどうかを確認します。
[14]:
sel = ar_select_order(yoy_housing, 13, glob=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 714
Model: Restr. AutoReg(13) Log Likelihood 589.177
Method: Conditional MLE S.D. of innovations 0.104
Date: Thu, 03 Oct 2024 AIC -1162.353
Time: 15:55:45 BIC -1125.933
Sample: 02-01-1961 HQIC -1148.276
- 06-01-2019
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
const 0.0035 0.004 0.875 0.382 -0.004 0.011
HOUSTNSA.L1 0.5640 0.035 16.167 0.000 0.496 0.632
HOUSTNSA.L2 0.2347 0.038 6.238 0.000 0.161 0.308
HOUSTNSA.L3 0.2051 0.037 5.560 0.000 0.133 0.277
HOUSTNSA.L7 -0.0903 0.030 -2.976 0.003 -0.150 -0.031
HOUSTNSA.L12 -0.3791 0.034 -11.075 0.000 -0.446 -0.312
HOUSTNSA.L13 0.3354 0.033 10.254 0.000 0.271 0.400
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 -1.0309 -0.2682j 1.0652 -0.4595
AR.2 -1.0309 +0.2682j 1.0652 0.4595
AR.3 -0.7454 -0.7417j 1.0515 -0.3754
AR.4 -0.7454 +0.7417j 1.0515 0.3754
AR.5 -0.3172 -1.0221j 1.0702 -0.2979
AR.6 -0.3172 +1.0221j 1.0702 0.2979
AR.7 0.2419 -1.0573j 1.0846 -0.2142
AR.8 0.2419 +1.0573j 1.0846 0.2142
AR.9 0.7840 -0.8303j 1.1420 -0.1296
AR.10 0.7840 +0.8303j 1.1420 0.1296
AR.11 1.0730 -0.2386j 1.0992 -0.0348
AR.12 1.0730 +0.2386j 1.0992 0.0348
AR.13 1.1193 -0.0000j 1.1193 -0.0000
------------------------------------------------------------------------------
[15]:
fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(fig=fig, lags=30)
季節ダミーを含めることもできます。モデルは前年比の変化を使用しているため、これらはすべて有意ではありません。
[16]:
sel = ar_select_order(yoy_housing, 13, glob=True, seasonal=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
====================================================================================
Dep. Variable: HOUSTNSA No. Observations: 714
Model: Restr. Seas. AutoReg(13) Log Likelihood 590.875
Method: Conditional MLE S.D. of innovations 0.104
Date: Thu, 03 Oct 2024 AIC -1143.751
Time: 16:08:11 BIC -1057.253
Sample: 02-01-1961 HQIC -1110.317
- 06-01-2019
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
const 0.0167 0.014 1.215 0.224 -0.010 0.044
s(2,12) -0.0179 0.019 -0.931 0.352 -0.056 0.020
s(3,12) -0.0121 0.019 -0.630 0.528 -0.050 0.026
s(4,12) -0.0210 0.019 -1.089 0.276 -0.059 0.017
s(5,12) -0.0223 0.019 -1.157 0.247 -0.060 0.015
s(6,12) -0.0224 0.019 -1.160 0.246 -0.060 0.015
s(7,12) -0.0212 0.019 -1.096 0.273 -0.059 0.017
s(8,12) -0.0101 0.019 -0.520 0.603 -0.048 0.028
s(9,12) -0.0095 0.019 -0.491 0.623 -0.047 0.028
s(10,12) -0.0049 0.019 -0.252 0.801 -0.043 0.033
s(11,12) -0.0084 0.019 -0.435 0.664 -0.046 0.030
s(12,12) -0.0077 0.019 -0.400 0.689 -0.046 0.030
HOUSTNSA.L1 0.5630 0.035 16.160 0.000 0.495 0.631
HOUSTNSA.L2 0.2347 0.038 6.248 0.000 0.161 0.308
HOUSTNSA.L3 0.2075 0.037 5.634 0.000 0.135 0.280
HOUSTNSA.L7 -0.0916 0.030 -3.013 0.003 -0.151 -0.032
HOUSTNSA.L12 -0.3810 0.034 -11.149 0.000 -0.448 -0.314
HOUSTNSA.L13 0.3373 0.033 10.327 0.000 0.273 0.401
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 -1.0305 -0.2681j 1.0648 -0.4595
AR.2 -1.0305 +0.2681j 1.0648 0.4595
AR.3 -0.7447 -0.7414j 1.0509 -0.3754
AR.4 -0.7447 +0.7414j 1.0509 0.3754
AR.5 -0.3172 -1.0215j 1.0696 -0.2979
AR.6 -0.3172 +1.0215j 1.0696 0.2979
AR.7 0.2416 -1.0568j 1.0841 -0.2142
AR.8 0.2416 +1.0568j 1.0841 0.2142
AR.9 0.7837 -0.8304j 1.1418 -0.1296
AR.10 0.7837 +0.8304j 1.1418 0.1296
AR.11 1.0724 -0.2383j 1.0986 -0.0348
AR.12 1.0724 +0.2383j 1.0986 0.0348
AR.13 1.1192 -0.0000j 1.1192 -0.0000
------------------------------------------------------------------------------
鉱工業生産¶
鉱工業生産指数データを使用して、予測を調べます。
[17]:
data = pdr.get_data_fred("INDPRO", "1959-01-01", "2019-06-01")
ind_prod = data.INDPRO.pct_change(12).dropna().asfreq("MS")
_, ax = plt.subplots(figsize=(16, 9))
ind_prod.plot(ax=ax)
[17]:
<Axes: xlabel='DATE'>
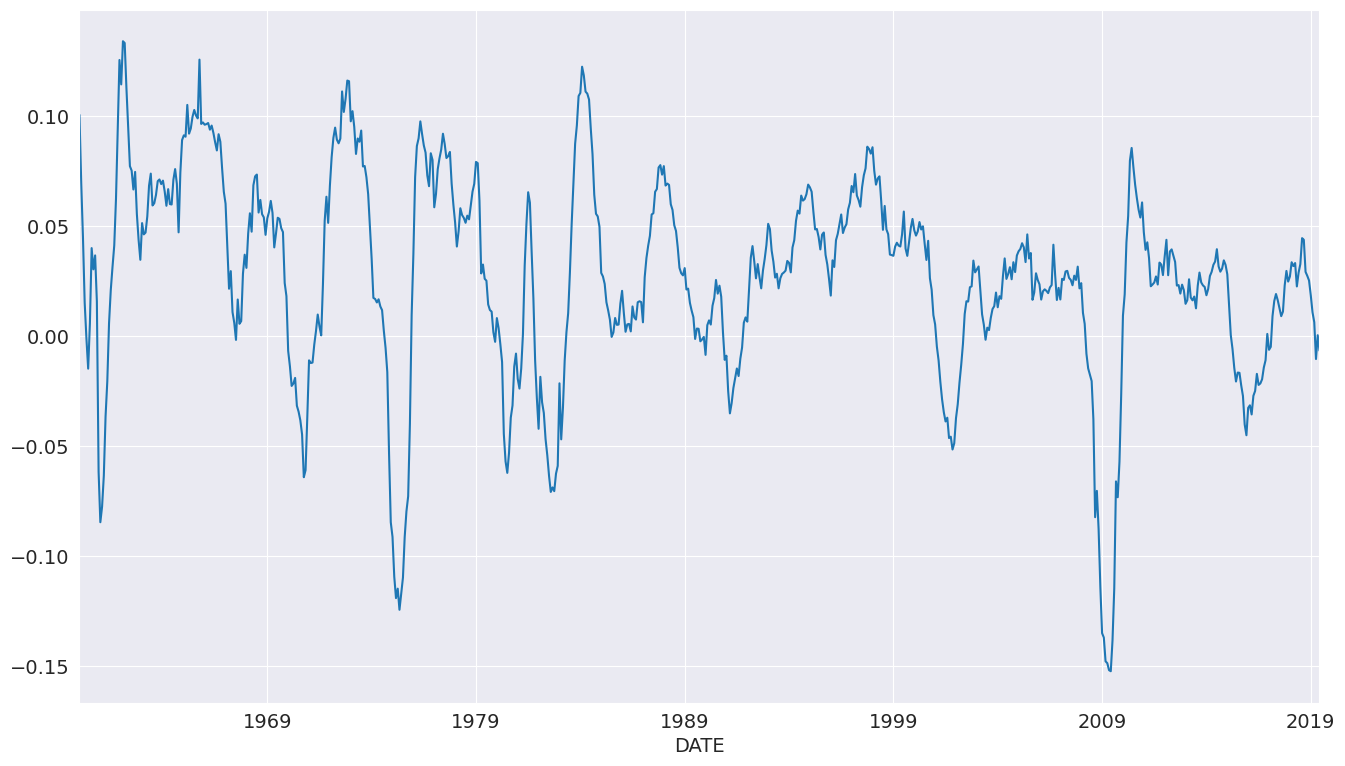
まず、最大12個のラグを使用してモデルを選択します。多くの係数が有意ではありませんが、AR(13)はBIC基準を最小化します。
[18]:
sel = ar_select_order(ind_prod, 13, "bic", old_names=False)
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: INDPRO No. Observations: 714
Model: AutoReg(13) Log Likelihood 2321.382
Method: Conditional MLE S.D. of innovations 0.009
Date: Thu, 03 Oct 2024 AIC -4612.763
Time: 16:08:12 BIC -4544.476
Sample: 02-01-1961 HQIC -4586.368
- 06-01-2019
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0012 0.000 2.783 0.005 0.000 0.002
INDPRO.L1 1.1577 0.035 33.179 0.000 1.089 1.226
INDPRO.L2 -0.0822 0.053 -1.543 0.123 -0.187 0.022
INDPRO.L3 7.041e-05 0.053 0.001 0.999 -0.104 0.104
INDPRO.L4 0.0076 0.053 0.143 0.886 -0.096 0.111
INDPRO.L5 -0.1329 0.053 -2.529 0.011 -0.236 -0.030
INDPRO.L6 -0.0080 0.052 -0.153 0.879 -0.111 0.095
INDPRO.L7 0.0556 0.052 1.064 0.287 -0.047 0.158
INDPRO.L8 -0.0296 0.052 -0.568 0.570 -0.132 0.073
INDPRO.L9 0.0920 0.052 1.770 0.077 -0.010 0.194
INDPRO.L10 -0.0808 0.052 -1.552 0.121 -0.183 0.021
INDPRO.L11 -0.0003 0.052 -0.005 0.996 -0.102 0.102
INDPRO.L12 -0.3820 0.052 -7.364 0.000 -0.484 -0.280
INDPRO.L13 0.3613 0.033 10.996 0.000 0.297 0.426
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 -1.0408 -0.2913j 1.0808 -0.4566
AR.2 -1.0408 +0.2913j 1.0808 0.4566
AR.3 -0.7803 -0.8039j 1.1204 -0.3726
AR.4 -0.7803 +0.8039j 1.1204 0.3726
AR.5 -0.2728 -1.0533j 1.0880 -0.2903
AR.6 -0.2728 +1.0533j 1.0880 0.2903
AR.7 0.2716 -1.0507j 1.0852 -0.2097
AR.8 0.2716 +1.0507j 1.0852 0.2097
AR.9 0.8010 -0.7285j 1.0827 -0.1175
AR.10 0.8010 +0.7285j 1.0827 0.1175
AR.11 1.0219 -0.2219j 1.0457 -0.0340
AR.12 1.0219 +0.2219j 1.0457 0.0340
AR.13 1.0560 -0.0000j 1.0560 -0.0000
------------------------------------------------------------------------------
グローバルサーチを使用することもできます。これにより、短いラグを必要とせずに、必要に応じてより長いラグを入力できます。ここでは、多くのラグが削除されています。モデルは、データに何らかの季節性がある可能性を示唆しています。
[19]:
sel = ar_select_order(ind_prod, 13, "bic", glob=True, old_names=False)
sel.ar_lags
res_glob = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: INDPRO No. Observations: 714
Model: AutoReg(13) Log Likelihood 2321.382
Method: Conditional MLE S.D. of innovations 0.009
Date: Thu, 03 Oct 2024 AIC -4612.763
Time: 16:08:14 BIC -4544.476
Sample: 02-01-1961 HQIC -4586.368
- 06-01-2019
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0012 0.000 2.783 0.005 0.000 0.002
INDPRO.L1 1.1577 0.035 33.179 0.000 1.089 1.226
INDPRO.L2 -0.0822 0.053 -1.543 0.123 -0.187 0.022
INDPRO.L3 7.041e-05 0.053 0.001 0.999 -0.104 0.104
INDPRO.L4 0.0076 0.053 0.143 0.886 -0.096 0.111
INDPRO.L5 -0.1329 0.053 -2.529 0.011 -0.236 -0.030
INDPRO.L6 -0.0080 0.052 -0.153 0.879 -0.111 0.095
INDPRO.L7 0.0556 0.052 1.064 0.287 -0.047 0.158
INDPRO.L8 -0.0296 0.052 -0.568 0.570 -0.132 0.073
INDPRO.L9 0.0920 0.052 1.770 0.077 -0.010 0.194
INDPRO.L10 -0.0808 0.052 -1.552 0.121 -0.183 0.021
INDPRO.L11 -0.0003 0.052 -0.005 0.996 -0.102 0.102
INDPRO.L12 -0.3820 0.052 -7.364 0.000 -0.484 -0.280
INDPRO.L13 0.3613 0.033 10.996 0.000 0.297 0.426
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 -1.0408 -0.2913j 1.0808 -0.4566
AR.2 -1.0408 +0.2913j 1.0808 0.4566
AR.3 -0.7803 -0.8039j 1.1204 -0.3726
AR.4 -0.7803 +0.8039j 1.1204 0.3726
AR.5 -0.2728 -1.0533j 1.0880 -0.2903
AR.6 -0.2728 +1.0533j 1.0880 0.2903
AR.7 0.2716 -1.0507j 1.0852 -0.2097
AR.8 0.2716 +1.0507j 1.0852 0.2097
AR.9 0.8010 -0.7285j 1.0827 -0.1175
AR.10 0.8010 +0.7285j 1.0827 0.1175
AR.11 1.0219 -0.2219j 1.0457 -0.0340
AR.12 1.0219 +0.2219j 1.0457 0.0340
AR.13 1.0560 -0.0000j 1.0560 -0.0000
------------------------------------------------------------------------------
`plot_predict` を使用して、信頼区間とともに予測プロットを作成できます。ここでは、最後の観測値から開始して18か月間続く予測を作成します.
[20]:
ind_prod.shape
[20]:
(714,)
[21]:
fig = res_glob.plot_predict(start=714, end=732)
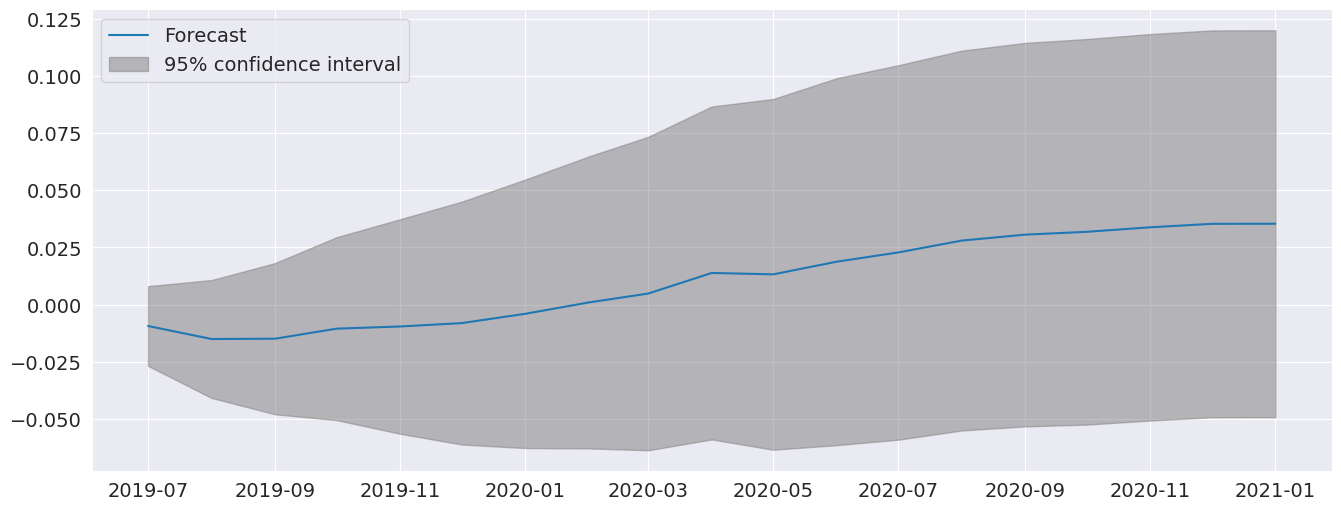
完全なモデルと制限付きモデルの予測は非常によく似ています。また、非常に異なるダイナミクスを持つAR(5)も含まれています。
[22]:
res_ar5 = AutoReg(ind_prod, 5, old_names=False).fit()
predictions = pd.DataFrame(
{
"AR(5)": res_ar5.predict(start=714, end=726),
"AR(13)": res.predict(start=714, end=726),
"Restr. AR(13)": res_glob.predict(start=714, end=726),
}
)
_, ax = plt.subplots()
ax = predictions.plot(ax=ax)
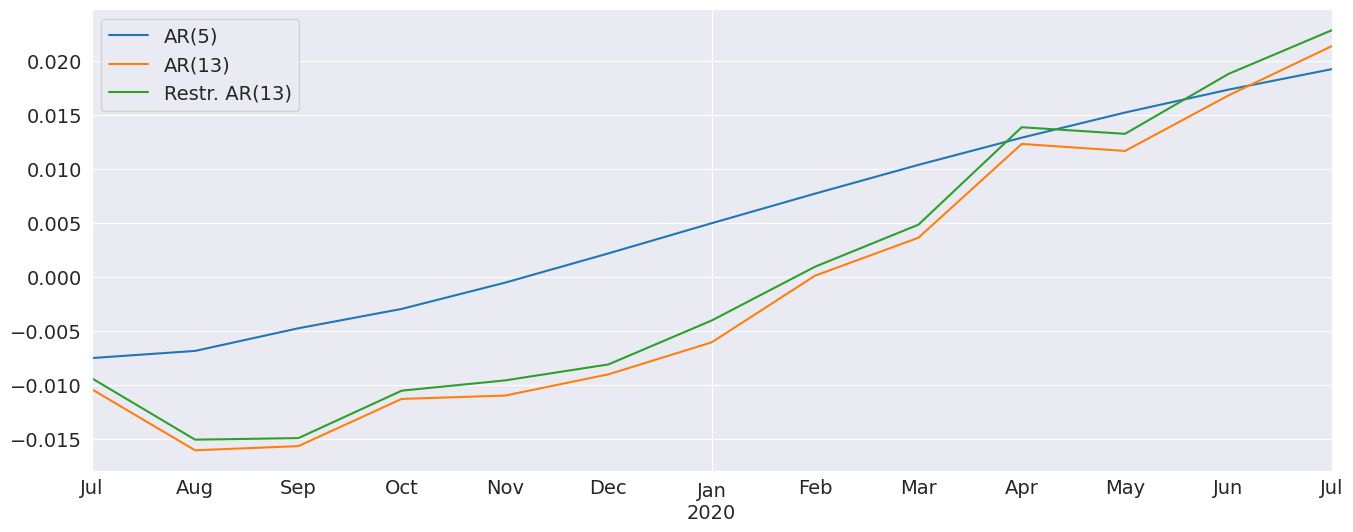
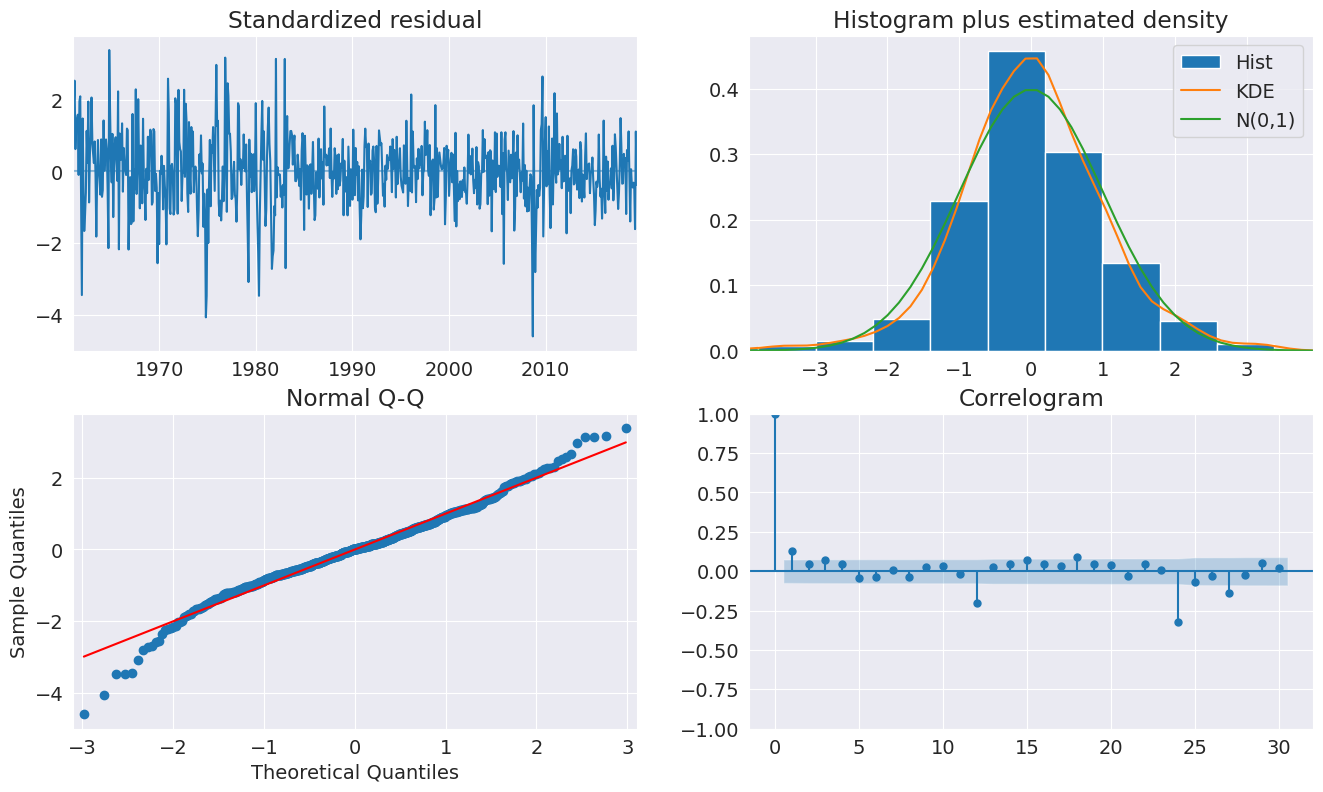
診断は、モデルがデータのダイナミクスのほとんどを捉えていることを示しています。ACFは季節周期におけるパターンを示しており、より完全な季節モデル(`SARIMAX`)が必要になる場合があります。
[23]:
fig = plt.figure(figsize=(16, 9))
fig = res_glob.plot_diagnostics(fig=fig, lags=30)
予測¶
予測は、結果インスタンスの `predict` メソッドを使用して生成されます。デフォルトでは、1ステップの予測である静的予測が生成されます。複数ステップの予測を生成するには、`dynamic=True` を使用する必要があります。
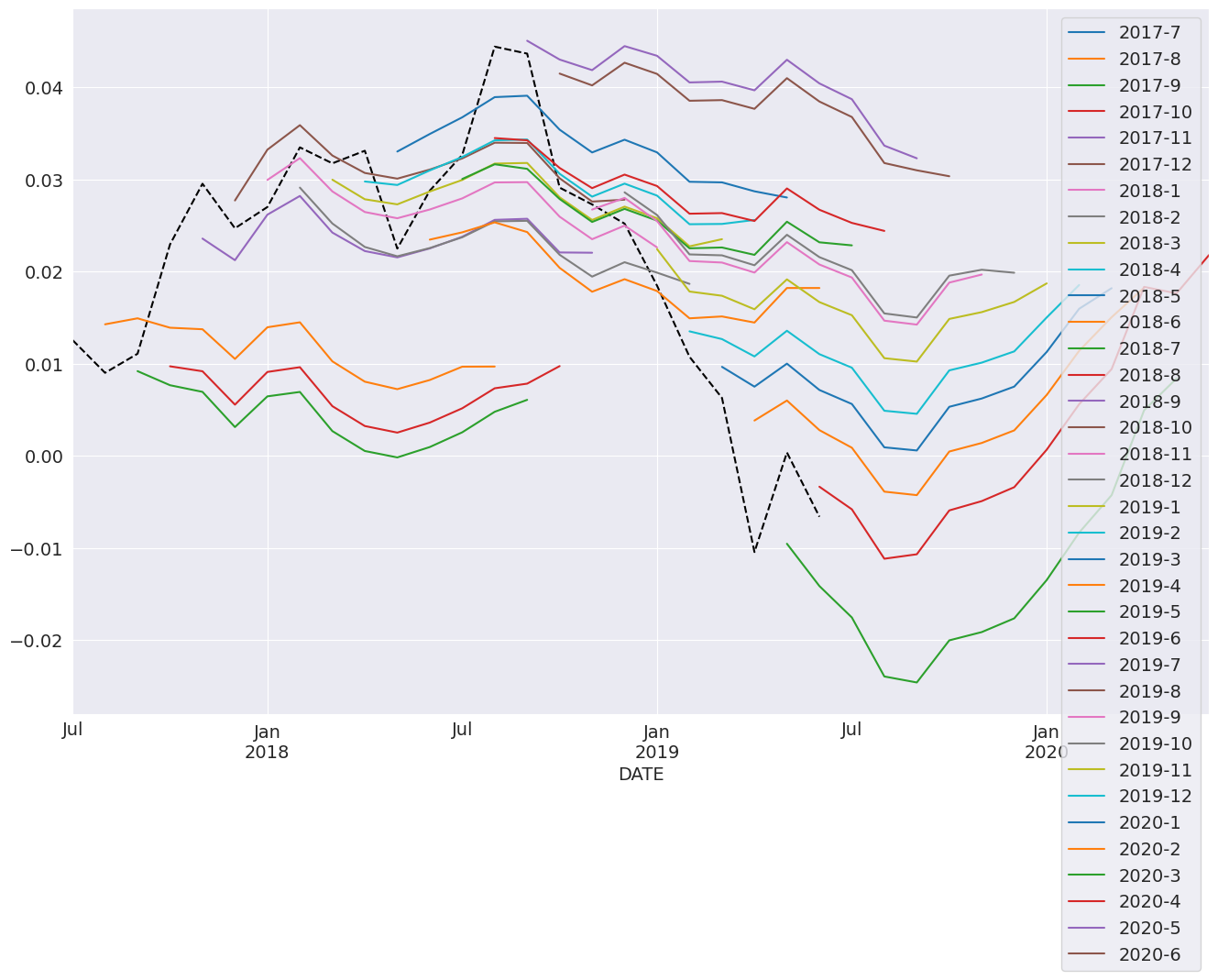
次のセルでは、サンプルの最後の24期間について、12ステップ先の予測を生成します。これにはループが必要です。
**注**: これらは技術的にはサンプル内です。なぜなら、予測に使用しているデータはパラメータの推定に使用されたからです。サンプル外の予測を作成するには、2つのモデルが必要です。1つ目は、サンプル外の期間を除外する必要があります。2つ目は、サンプル外の期間を除外した短いサンプルモデルのパラメータを使用して、フルサンプルモデルの `predict` メソッドを使用します。
[24]:
import numpy as np
start = ind_prod.index[-24]
forecast_index = pd.date_range(start, freq=ind_prod.index.freq, periods=36)
cols = ["-".join(str(val) for val in (idx.year, idx.month)) for idx in forecast_index]
forecasts = pd.DataFrame(index=forecast_index, columns=cols)
for i in range(1, 24):
fcast = res_glob.predict(
start=forecast_index[i], end=forecast_index[i + 12], dynamic=True
)
forecasts.loc[fcast.index, cols[i]] = fcast
_, ax = plt.subplots(figsize=(16, 10))
ind_prod.iloc[-24:].plot(ax=ax, color="black", linestyle="--")
ax = forecasts.plot(ax=ax)
SARIMAXとの比較¶
`SARIMAX` は、外生回帰変数を持つ季節自己回帰和分移動平均モデルの実装です。以下をサポートしています。
季節および非季節ARおよびMA成分の指定
外生変数の包含
カルマンフィルターを使用した完全最尤推定
このモデルは、`AutoReg` よりも機能が豊富です。`SARIMAX` とは異なり、`AutoReg` はOLSを使用してパラメータを推定します。これは高速であり、問題はグローバルに凸であるため、局所解の問題はありません。閉形式推定量とそのパフォーマンスは、AR(P)モデルを比較する場合の `AutoReg` の `SARIMAX` に対する主な利点です。`AutoReg` は季節ダミーもサポートしており、ユーザーが外生回帰変数として含めれば `SARIMAX` と一緒に使用できます。
[25]:
from statsmodels.tsa.api import SARIMAX
sarimax_mod = SARIMAX(ind_prod, order=((1, 5, 12, 13), 0, 0), trend="c")
sarimax_res = sarimax_mod.fit()
print(sarimax_res.summary())
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 6 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= -3.21907D+00 |proj g|= 1.78480D+01
This problem is unconstrained.
At iterate 5 f= -3.22490D+00 |proj g|= 1.52242D-01
At iterate 10 f= -3.22526D+00 |proj g|= 1.46006D+00
At iterate 15 f= -3.22550D+00 |proj g|= 7.46711D-01
At iterate 20 f= -3.22610D+00 |proj g|= 2.52890D-01
At iterate 25 f= -3.22611D+00 |proj g|= 1.80088D-01
At iterate 30 f= -3.22646D+00 |proj g|= 1.46895D+00
At iterate 35 f= -3.22677D+00 |proj g|= 1.05336D-01
At iterate 40 f= -3.22678D+00 |proj g|= 3.20093D-02
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
6 41 64 1 0 0 3.201D-02 -3.227D+00
F = -3.2267786140514940
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
SARIMAX Results
=========================================================================================
Dep. Variable: INDPRO No. Observations: 714
Model: SARIMAX([1, 5, 12, 13], 0, 0) Log Likelihood 2303.920
Date: Thu, 03 Oct 2024 AIC -4595.840
Time: 16:08:18 BIC -4568.415
Sample: 01-01-1960 HQIC -4585.248
- 06-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.0011 0.000 2.534 0.011 0.000 0.002
ar.L1 1.0801 0.010 107.331 0.000 1.060 1.100
ar.L5 -0.0847 0.011 -7.592 0.000 -0.107 -0.063
ar.L12 -0.4428 0.026 -17.302 0.000 -0.493 -0.393
ar.L13 0.4073 0.025 16.213 0.000 0.358 0.457
sigma2 9.136e-05 3.08e-06 29.630 0.000 8.53e-05 9.74e-05
===================================================================================
Ljung-Box (L1) (Q): 21.77 Jarque-Bera (JB): 959.65
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 0.37 Skew: -0.63
Prob(H) (two-sided): 0.00 Kurtosis: 8.54
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Warning: more than 10 function and gradient
evaluations in the last line search. Termination
may possibly be caused by a bad search direction.
[26]:
sarimax_params = sarimax_res.params.iloc[:-1].copy()
sarimax_params.index = res_glob.params.index
params = pd.concat([res_glob.params, sarimax_params], axis=1, sort=False)
params.columns = ["AutoReg", "SARIMAX"]
params
[26]:
| AutoReg | SARIMAX | |
|---|---|---|
| 定数 | 0.001234 | 0.001085 |
| INDPRO.L1 | 1.088761 | 1.080116 |
| INDPRO.L5 | -0.105665 | -0.084738 |
| INDPRO.L12 | -0.388374 | -0.442793 |
| INDPRO.L13 | 0.362319 | 0.407338 |
カスタム決定論的プロセス¶
deterministic パラメータを使用すると、カスタムの DeterministicProcess を使用できます。これにより、より複雑な決定論的項を構築できます。たとえば、2 つの周期を持つ季節成分を含む項や、次の例に示すように、季節ダミーではなくフーリエ級数を使用する項などです。
[27]:
from statsmodels.tsa.deterministic import DeterministicProcess
dp = DeterministicProcess(housing.index, constant=True, period=12, fourier=2)
mod = AutoReg(housing, 2, trend="n", seasonal=False, deterministic=dp)
res = mod.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: AutoReg(2) Log Likelihood -2716.505
Method: Conditional MLE S.D. of innovations 10.364
Date: Thu, 03 Oct 2024 AIC 5449.010
Time: 16:08:18 BIC 5485.677
Sample: 04-01-1959 HQIC 5463.163
- 06-01-2019
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 1.7550 0.391 4.485 0.000 0.988 2.522
sin(1,12) 16.7443 0.860 19.478 0.000 15.059 18.429
cos(1,12) 4.9409 0.588 8.409 0.000 3.789 6.093
sin(2,12) 12.9364 0.619 20.889 0.000 11.723 14.150
cos(2,12) -0.4738 0.754 -0.628 0.530 -1.952 1.004
HOUSTNSA.L1 -0.3905 0.037 -10.664 0.000 -0.462 -0.319
HOUSTNSA.L2 -0.1746 0.037 -4.769 0.000 -0.246 -0.103
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -1.1182 -2.1159j 2.3932 -0.3274
AR.2 -1.1182 +2.1159j 2.3932 0.3274
-----------------------------------------------------------------------------
[28]:
fig = res.plot_predict(720, 840)