線形混合効果モデル¶
[1]:
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.tools.sm_exceptions import ConvergenceWarning
**注記**: このノートブックのRコードと結果は、Rなしでドキュメントをビルドできるようにマークダウンに変換されています。ノートブックのRの結果は、R 3.5.1とlme4 1.1を使用して計算されました。
%load_ext rpy2.ipython
%R library(lme4)
array(['lme4', 'Matrix', 'tools', 'stats', 'graphics', 'grDevices',
'utils', 'datasets', 'methods', 'base'], dtype='<U9')
RのlmerとstatsmodelsのMixedLMの比較¶
線形混合モデル(MixedLM)のstatsmodels実装は、Lindstrom and Bates(JASA 1988)で概説されているアプローチに厳密に従っています。これは、RパッケージLME4でも採用されているアプローチです。この分野の基本的な手法はほとんど成熟しているので、Stata、SASなどの他のパッケージもこのアプローチと一致しているはずです。
ここでは、statsmodelsのMixedLMプロシージャを使用して線形混合モデルを適合させる方法を示します。比較のために、R(LME4)の結果が含まれています。
インポート文を以下に示します。
豚の成長曲線¶
これらは、要因計画法による縦断データです。結果変数は各豚の体重であり、ここで使用する唯一の予測変数は「時間」です。最初に、各豚のランダム切片を使用して、平均体重を時間の線形関数として表すモデルを適合させます。モデルは式を使用して指定されます。ランダム効果の構造は指定されていないため、デフォルトのランダム効果構造(各グループのランダム切片)が自動的に使用されます。
[2]:
data = sm.datasets.get_rdataset("dietox", "geepack").data
md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"])
mdf = md.fit(method=["lbfgs"])
print(mdf.summary())
Mixed Linear Model Regression Results
========================================================
Model: MixedLM Dependent Variable: Weight
No. Observations: 861 Method: REML
No. Groups: 72 Scale: 11.3669
Min. group size: 11 Log-Likelihood: -2404.7753
Max. group size: 12 Converged: Yes
Mean group size: 12.0
--------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
--------------------------------------------------------
Intercept 15.724 0.788 19.952 0.000 14.179 17.268
Time 6.943 0.033 207.939 0.000 6.877 7.008
Group Var 40.395 2.149
========================================================
LMERを使用してRで適合させた同じモデルを以下に示します。
%%R
data(dietox, package='geepack')
%R print(summary(lmer('Weight ~ Time + (1|Pig)', data=dietox)))
Linear mixed model fit by REML ['lmerMod']
Formula: Weight ~ Time + (1 | Pig)
Data: dietox
REML criterion at convergence: 4809.6
Scaled residuals:
Min 1Q Median 3Q Max
-4.7118 -0.5696 -0.0943 0.4877 4.7732
Random effects:
Groups Name Variance Std.Dev.
Pig (Intercept) 40.39 6.356
Residual 11.37 3.371
Number of obs: 861, groups: Pig, 72
Fixed effects:
Estimate Std. Error t value
(Intercept) 15.72352 0.78805 19.95
Time 6.94251 0.03339 207.94
Correlation of Fixed Effects:
(Intr)
Time -0.275
statsmodelsの結果の概要では、固定効果とランダム効果のパラメーター推定値が1つのテーブルに表示されていることに注意してください。動物のランダム効果は、上記のstatsmodelsの出力では「Intercept RE」とラベル付けされています。LME4の出力では、この効果はランダム効果セクションの豚の切片です。
ランダム効果の分散と共分散パラメーターの標準誤差が有用かどうかについては、多くの議論がありました。LME4では、これらの標準誤差は表示されません。これは、パッケージの作成者がそれらがそれほど有益ではないと考えているためです。その有用性には疑問符が付きますが、標準誤差をサマリーテーブルに含めることにしました。ただし、対応するWald信頼区間は表示しません。
次に、各動物に2つのランダム効果を持つモデルを適合させます。ランダム切片とランダムな傾き(時間に関して)です。これは、各豚の基準体重が異なり、成長速度も異なる可能性があることを意味します。「時間」はランダム係数を持つ共変量であると式で指定されています。デフォルトでは、式には常に切片が含まれます(ここでは、式として「0 + Time」を使用することで抑制できます)。
[3]:
md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"], re_formula="~Time")
mdf = md.fit(method=["lbfgs"])
print(mdf.summary())
Mixed Linear Model Regression Results
===========================================================
Model: MixedLM Dependent Variable: Weight
No. Observations: 861 Method: REML
No. Groups: 72 Scale: 6.0372
Min. group size: 11 Log-Likelihood: -2217.0475
Max. group size: 12 Converged: Yes
Mean group size: 12.0
-----------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
-----------------------------------------------------------
Intercept 15.739 0.550 28.603 0.000 14.660 16.817
Time 6.939 0.080 86.925 0.000 6.783 7.095
Group Var 19.503 1.561
Group x Time Cov 0.294 0.153
Time Var 0.416 0.033
===========================================================
RのLMERを使用して適合させた同じモデルを以下に示します。
%R print(summary(lmer("Weight ~ Time + (1 + Time | Pig)", data=dietox)))
Linear mixed model fit by REML ['lmerMod']
Formula: Weight ~ Time + (1 + Time | Pig)
Data: dietox
REML criterion at convergence: 4434.1
Scaled residuals:
Min 1Q Median 3Q Max
-6.4286 -0.5529 -0.0416 0.4841 3.5624
Random effects:
Groups Name Variance Std.Dev. Corr
Pig (Intercept) 19.493 4.415
Time 0.416 0.645 0.10
Residual 6.038 2.457
Number of obs: 861, groups: Pig, 72
Fixed effects:
Estimate Std. Error t value
(Intercept) 15.73865 0.55012 28.61
Time 6.93901 0.07982 86.93
Correlation of Fixed Effects:
(Intr)
Time 0.006
ランダム切片とランダムな傾きは、わずかに相関しています \((0.294 / \sqrt{19.493 * 0.416} \approx 0.1)\)。そのため、次に、2つのランダム効果が相関しないように制約されたモデルを適合させます。
[4]:
0.294 / (19.493 * 0.416) ** 0.5
[4]:
0.10324316832591753
[5]:
md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"], re_formula="~Time")
free = sm.regression.mixed_linear_model.MixedLMParams.from_components(
np.ones(2), np.eye(2)
)
mdf = md.fit(free=free, method=["lbfgs"])
print(mdf.summary())
Mixed Linear Model Regression Results
===========================================================
Model: MixedLM Dependent Variable: Weight
No. Observations: 861 Method: REML
No. Groups: 72 Scale: 6.0283
Min. group size: 11 Log-Likelihood: -2217.3481
Max. group size: 12 Converged: Yes
Mean group size: 12.0
-----------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
-----------------------------------------------------------
Intercept 15.739 0.554 28.388 0.000 14.652 16.825
Time 6.939 0.080 86.248 0.000 6.781 7.097
Group Var 19.837 1.571
Group x Time Cov 0.000 0.000
Time Var 0.423 0.033
===========================================================
相関パラメーターを0に固定すると、尤度が0.3低下します。2 x 0.3 = 0.6を自由度1のカイ二乗基準分布と比較すると、このパラメーターが0であるモデルとデータが非常によく一致していることが示唆されます。
RのLMERを使用して適合させた同じモデルを以下に示します(ここでは、Rは尤度の代わりにREML基準を報告しており、REML基準は対数尤度の2倍です)。
%R print(summary(lmer("Weight ~ Time + (1 | Pig) + (0 + Time | Pig)", data=dietox)))
Linear mixed model fit by REML ['lmerMod']
Formula: Weight ~ Time + (1 | Pig) + (0 + Time | Pig)
Data: dietox
REML criterion at convergence: 4434.7
Scaled residuals:
Min 1Q Median 3Q Max
-6.4281 -0.5527 -0.0405 0.4840 3.5661
Random effects:
Groups Name Variance Std.Dev.
Pig (Intercept) 19.8404 4.4543
Pig.1 Time 0.4234 0.6507
Residual 6.0282 2.4552
Number of obs: 861, groups: Pig, 72
Fixed effects:
Estimate Std. Error t value
(Intercept) 15.73875 0.55444 28.39
Time 6.93899 0.08045 86.25
Correlation of Fixed Effects:
(Intr)
Time -0.086
シトカトウヒの成長データ¶
これは、LMER Rライブラリで提供されているサンプルデータセットの1つです。結果変数は木のサイズであり、ここで使用される共変量は時間値です。データは木ごとにグループ化されています。
[6]:
data = sm.datasets.get_rdataset("Sitka", "MASS").data
endog = data["size"]
data["Intercept"] = 1
exog = data[["Intercept", "Time"]]
ランダム切片を持つ基本モデルのstatsmodels LME適合を以下に示します。endogデータとexogデータを配列としてLME init関数に直接渡しています。また、endog_reは引数4でランダム切片として明示的に指定されています(指定されていない場合でもデフォルトになります)。
[7]:
md = sm.MixedLM(endog, exog, groups=data["tree"], exog_re=exog["Intercept"])
mdf = md.fit()
print(mdf.summary())
Mixed Linear Model Regression Results
=======================================================
Model: MixedLM Dependent Variable: size
No. Observations: 395 Method: REML
No. Groups: 79 Scale: 0.0392
Min. group size: 5 Log-Likelihood: -82.3884
Max. group size: 5 Converged: Yes
Mean group size: 5.0
-------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
-------------------------------------------------------
Intercept 2.273 0.088 25.864 0.000 2.101 2.446
Time 0.013 0.000 47.796 0.000 0.012 0.013
Intercept Var 0.374 0.345
=======================================================
LMERを使用してRで適合させた同じモデルを以下に示します。
%R
data(Sitka, package="MASS")
print(summary(lmer("size ~ Time + (1 | tree)", data=Sitka)))
Linear mixed model fit by REML ['lmerMod']
Formula: size ~ Time + (1 | tree)
Data: Sitka
REML criterion at convergence: 164.8
Scaled residuals:
Min 1Q Median 3Q Max
-2.9979 -0.5169 0.1576 0.5392 4.4012
Random effects:
Groups Name Variance Std.Dev.
tree (Intercept) 0.37451 0.612
Residual 0.03921 0.198
Number of obs: 395, groups: tree, 79
Fixed effects:
Estimate Std. Error t value
(Intercept) 2.2732443 0.0878955 25.86
Time 0.0126855 0.0002654 47.80
Correlation of Fixed Effects:
(Intr)
Time -0.611
ランダムな傾きを追加してみましょう。今回はRから始めます。以下のコードと出力から、ランダムな傾きの分散のREML推定値がほぼゼロであることがわかります。
%R print(summary(lmer("size ~ Time + (1 + Time | tree)", data=Sitka)))
Linear mixed model fit by REML ['lmerMod']
Formula: size ~ Time + (1 + Time | tree)
Data: Sitka
REML criterion at convergence: 153.4
Scaled residuals:
Min 1Q Median 3Q Max
-2.7609 -0.5173 0.1188 0.5270 3.5466
Random effects:
Groups Name Variance Std.Dev. Corr
tree (Intercept) 2.217e-01 0.470842
Time 3.288e-06 0.001813 -0.17
Residual 3.634e-02 0.190642
Number of obs: 395, groups: tree, 79
Fixed effects:
Estimate Std. Error t value
(Intercept) 2.273244 0.074655 30.45
Time 0.012686 0.000327 38.80
Correlation of Fixed Effects:
(Intr)
Time -0.615
convergence code: 0
Model failed to converge with max|grad| = 0.793203 (tol = 0.002, component 1)
Model is nearly unidentifiable: very large eigenvalue
- Rescale variables?
statsmodels LMEでデフォルトでこれを実行すると、分散推定値が tatsächlich sehr klein であることがわかります。これは、解がパラメーター空間の境界上にあるという警告につながります。回帰の傾きはRと非常によく一致していますが、尤度値はRによって返される値よりもはるかに高くなっています。
[8]:
exog_re = exog.copy()
md = sm.MixedLM(endog, exog, data["tree"], exog_re)
mdf = md.fit()
print(mdf.summary())
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/regression/mixed_linear_model.py:2237: ConvergenceWarning: The MLE may be on the boundary of the parameter space.
warnings.warn(msg, ConvergenceWarning)
Mixed Linear Model Regression Results
===============================================================
Model: MixedLM Dependent Variable: size
No. Observations: 395 Method: REML
No. Groups: 79 Scale: 0.0264
Min. group size: 5 Log-Likelihood: -62.4834
Max. group size: 5 Converged: Yes
Mean group size: 5.0
---------------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
---------------------------------------------------------------
Intercept 2.273 0.101 22.513 0.000 2.075 2.471
Time 0.013 0.000 33.888 0.000 0.012 0.013
Intercept Var 0.646 0.914
Intercept x Time Cov -0.001 0.003
Time Var 0.000 0.000
===============================================================
プロファイル尤度のプロットを作成することにより、ランダム効果の構造をさらに詳しく調べることができます。ランダム切片から始め、MLEより0.1単位下から0.1単位上までのプロファイル尤度のプロットを生成します。プロファイル尤度内の各最適化では警告が発生するため(ランダムな傾きの分散がゼロに近いことが原因)、ここでは警告をオフにします。
[9]:
import warnings
with warnings.catch_warnings():
warnings.filterwarnings("ignore")
likev = mdf.profile_re(0, "re", dist_low=0.1, dist_high=0.1)
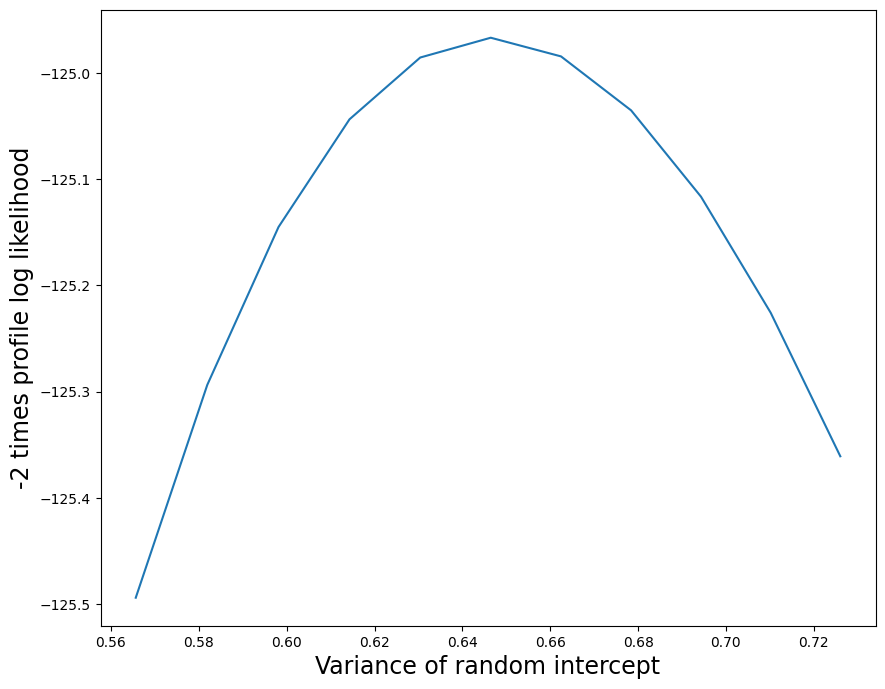
プロファイル尤度関数のプロットを以下に示します。対数尤度差に2を掛けて、自由度1の通常の \(\chi^2\) 基準分布を取得します。
[10]:
import matplotlib.pyplot as plt
[11]:
plt.figure(figsize=(10, 8))
plt.plot(likev[:, 0], 2 * likev[:, 1])
plt.xlabel("Variance of random intercept", size=17)
plt.ylabel("-2 times profile log likelihood", size=17)
[11]:
Text(0, 0.5, '-2 times profile log likelihood')
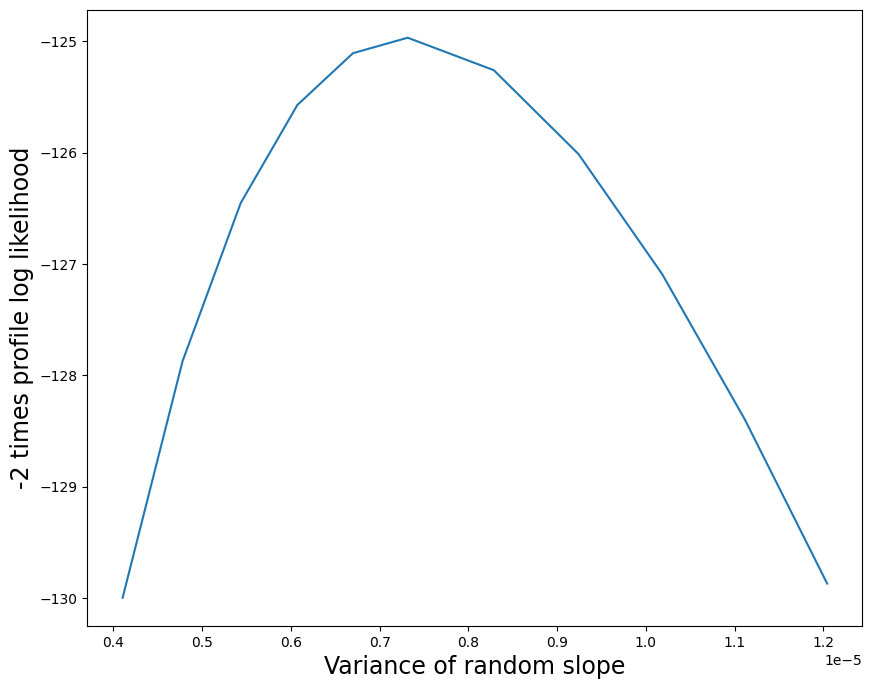
プロファイル尤度関数のプロットを以下に示します。プロファイル尤度プロットは、ランダムな傾きの分散パラメーターのMLEが非常に小さい正の数であり、この推定値の不確実性が低いことを示しています。
[12]:
re = mdf.cov_re.iloc[1, 1]
with warnings.catch_warnings():
# Parameter is often on the boundary
warnings.simplefilter("ignore", ConvergenceWarning)
likev = mdf.profile_re(1, "re", dist_low=0.5 * re, dist_high=0.8 * re)
plt.figure(figsize=(10, 8))
plt.plot(likev[:, 0], 2 * likev[:, 1])
plt.xlabel("Variance of random slope", size=17)
lbl = plt.ylabel("-2 times profile log likelihood", size=17)