マルコフスイッチング自己回帰モデル¶
このノートブックでは、statsmodelsにおけるマルコフスイッチングモデルの使用例として、キムとネルソン(1999)で発表されたいくつかの結果を再現します。ハミルトン(1989)のフィルターとキム(1994)のスムーザーを適用します。
これは、http://www.eviews.com/EViews8/ev8ecswitch_n.html#MarkovARにあるE-views 8のマルコフスイッチングモデル、またはhttp://www.stata.com/manuals14/tsmswitch.pdfにあるStata 14のマルコフスイッチングモデルに対してテストされています。
[1]:
%matplotlib inline
from datetime import datetime
from io import BytesIO
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import requests
import statsmodels.api as sm
# NBER recessions
from pandas_datareader.data import DataReader
usrec = DataReader(
"USREC", "fred", start=datetime(1947, 1, 1), end=datetime(2013, 4, 1)
)
GNPのハミルトン(1989)スイッチングモデル¶
これは、マルコフスイッチングモデルを紹介したハミルトン(1989)の画期的な論文を再現したものです。このモデルは、プロセスの平均が2つのレジーム間で切り替わる4次の自己回帰モデルです。以下のように記述できます。
各期間において、レジームは以下の遷移確率行列に従って遷移します。
ここで、\(p_{ij}\)は、レジーム\(i\)からレジーム\(j\)へ遷移する確率です。
このモデルクラスは、statsmodelsの時系列部分にあるMarkovAutoregressionです。モデルを作成するためには、k_regimes=2でレジーム数を、order=4で自己回帰の次数を指定する必要があります。デフォルトのモデルには、スイッチング自己回帰係数も含まれているため、ここではswitching_ar=Falseを指定して、それらを回避する必要があります。
作成後、モデルは最尤推定によってfitされます。内部では、期待値最大化(EM)アルゴリズムのいくつかのステップを使用して適切な初期パラメータが検出され、準ニュートン(BFGS)アルゴリズムが適用されて最大値が迅速に検出されます。
[2]:
import requests
import shutil
def download_file(url):
local_filename = url.split('/')[-1]
with requests.get(url, stream=True) as r:
with open(local_filename, 'wb') as f:
shutil.copyfileobj(r.raw, f)
return local_filename
filename = download_file("https://www.stata-press.com/data/r14/rgnp.dta")
# Get the RGNP data to replicate Hamilton
dta = pd.read_stata(filename).iloc[1:]
dta.index = pd.DatetimeIndex(dta.date, freq="QS")
dta_hamilton = dta.rgnp
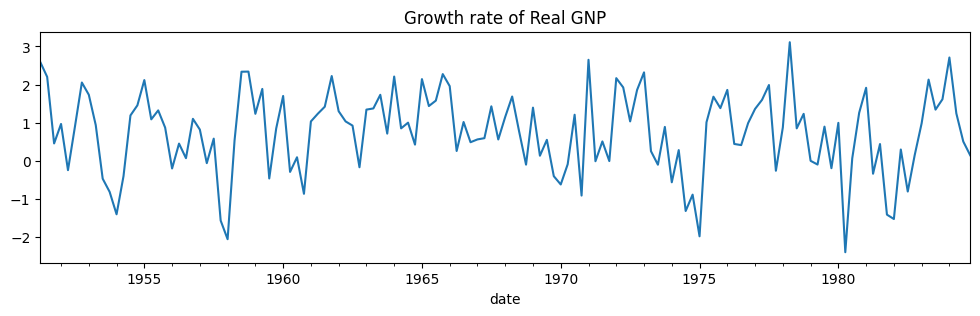
# Plot the data
dta_hamilton.plot(title="Growth rate of Real GNP", figsize=(12, 3))
# Fit the model
mod_hamilton = sm.tsa.MarkovAutoregression(
dta_hamilton, k_regimes=2, order=4, switching_ar=False
)
res_hamilton = mod_hamilton.fit()
[3]:
res_hamilton.summary()
[3]:
| 従属変数 | rgnp | 観測数 | 131 |
|---|---|---|---|
| モデル | MarkovAutoregression | 対数尤度 | -181.263 |
| 日付 | 2024年10月3日(木) | AIC | 380.527 |
| 時間 | 15:44:58 | BIC | 406.404 |
| サンプル | 04-01-1951 | HQIC | 391.042 |
| - 10-01-1984 | |||
| 共分散タイプ | 近似 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | -0.3588 | 0.265 | -1.356 | 0.175 | -0.877 | 0.160 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 1.1635 | 0.075 | 15.614 | 0.000 | 1.017 | 1.310 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2 | 0.5914 | 0.103 | 5.761 | 0.000 | 0.390 | 0.793 |
| ar.L1 | 0.0135 | 0.120 | 0.112 | 0.911 | -0.222 | 0.249 |
| ar.L2 | -0.0575 | 0.138 | -0.418 | 0.676 | -0.327 | 0.212 |
| ar.L3 | -0.2470 | 0.107 | -2.310 | 0.021 | -0.457 | -0.037 |
| ar.L4 | -0.2129 | 0.111 | -1.926 | 0.054 | -0.430 | 0.004 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| p[0->0] | 0.7547 | 0.097 | 7.819 | 0.000 | 0.565 | 0.944 |
| p[1->0] | 0.0959 | 0.038 | 2.542 | 0.011 | 0.022 | 0.170 |
警告
[1] 共分散行列は数値微分(複素ステップ)を使用して計算されました。
ここでは、景気後退のフィルター処理された確率と平滑化された確率をプロットします。フィルター処理とは、\(t\)時点までのデータに基づいて(ただし、\(t+1, ..., T\)時点を除く)、\(t\)時点での確率の推定値を指します。平滑化とは、サンプル内のすべてのデータを使用して、\(t\)時点での確率の推定値を指します。
参考までに、網掛けされた期間はNBERの景気後退を表しています。
[4]:
fig, axes = plt.subplots(2, figsize=(7, 7))
ax = axes[0]
ax.plot(res_hamilton.filtered_marginal_probabilities[0])
ax.fill_between(usrec.index, 0, 1, where=usrec["USREC"].values, color="k", alpha=0.1)
ax.set_xlim(dta_hamilton.index[4], dta_hamilton.index[-1])
ax.set(title="Filtered probability of recession")
ax = axes[1]
ax.plot(res_hamilton.smoothed_marginal_probabilities[0])
ax.fill_between(usrec.index, 0, 1, where=usrec["USREC"].values, color="k", alpha=0.1)
ax.set_xlim(dta_hamilton.index[4], dta_hamilton.index[-1])
ax.set(title="Smoothed probability of recession")
fig.tight_layout()
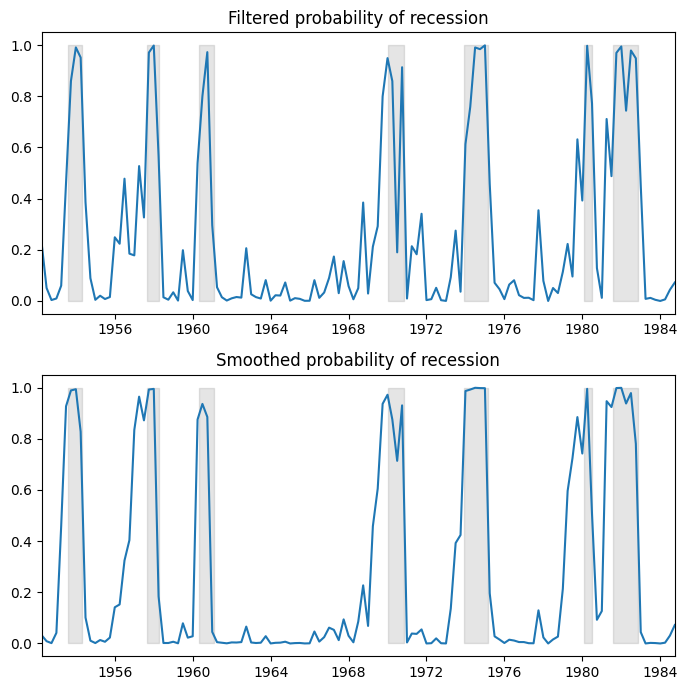
推定された遷移行列から、景気後退と景気拡大の予想される期間を計算できます。
[5]:
print(res_hamilton.expected_durations)
[ 4.07604744 10.42589389]
この場合、景気後退は約1年(4四半期)続き、景気拡大は約2年半続くと予想されます。
キム、ネルソン、スタートツ(1998)3状態分散スイッチング¶
このモデルは、レジーム異分散(分散の切り替え)があり、平均効果がない場合の推定を示します。データセットはhttp://econ.korea.ac.kr/~cjkim/MARKOV/data/ew_excs.prnで入手できます。
問題のモデルは次のとおりです。
自己回帰成分がないため、このモデルはMarkovRegressionクラスを使用して適合させることができます。平均効果がないため、trend='n'を指定します。切り替え分散には3つのレジームがあると仮定されているため、k_regimes=3とswitching_variance=Trueを指定します(デフォルトでは、分散はすべてのレジームで同じであると仮定されます)。
[6]:
# Get the dataset
ew_excs = requests.get("http://econ.korea.ac.kr/~cjkim/MARKOV/data/ew_excs.prn").content
raw = pd.read_table(BytesIO(ew_excs), header=None, skipfooter=1, engine="python")
raw.index = pd.date_range("1926-01-01", "1995-12-01", freq="MS")
dta_kns = raw.loc[:"1986"] - raw.loc[:"1986"].mean()
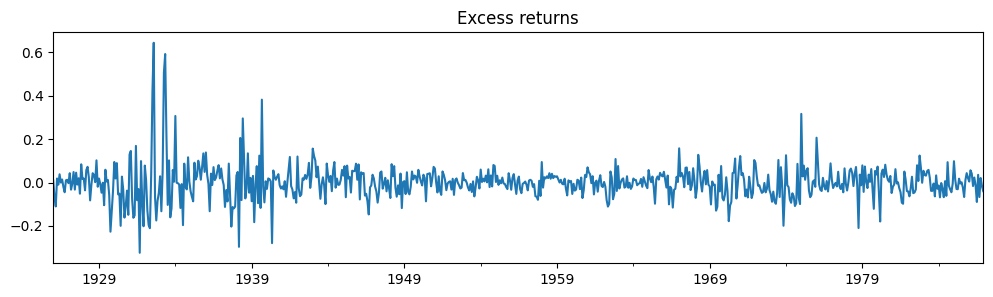
# Plot the dataset
dta_kns[0].plot(title="Excess returns", figsize=(12, 3))
# Fit the model
mod_kns = sm.tsa.MarkovRegression(
dta_kns, k_regimes=3, trend="n", switching_variance=True
)
res_kns = mod_kns.fit()
[7]:
res_kns.summary()
[7]:
| 従属変数 | 0 | 観測数 | 732 |
|---|---|---|---|
| モデル | MarkovRegression | 対数尤度 | 1001.895 |
| 日付 | 2024年10月3日(木) | AIC | -1985.790 |
| 時間 | 15:45:03 | BIC | -1944.428 |
| サンプル | 01-01-1926 | HQIC | -1969.834 |
| - 12-01-1986 | |||
| 共分散タイプ | 近似 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2 | 0.0012 | 0.000 | 7.136 | 0.000 | 0.001 | 0.002 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2 | 0.0040 | 0.000 | 8.489 | 0.000 | 0.003 | 0.005 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2 | 0.0311 | 0.006 | 5.461 | 0.000 | 0.020 | 0.042 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| p[0->0] | 0.9747 | 0.000 | 7857.416 | 0.000 | 0.974 | 0.975 |
| p[1->0] | 0.0195 | 0.010 | 1.949 | 0.051 | -0.000 | 0.039 |
| p[2->0] | 2.354e-08 | nan | nan | nan | nan | nan |
| p[0->1] | 0.0253 | 3.97e-05 | 637.835 | 0.000 | 0.025 | 0.025 |
| p[1->1] | 0.9688 | 0.013 | 75.528 | 0.000 | 0.944 | 0.994 |
| p[2->1] | 0.0493 | 0.032 | 1.551 | 0.121 | -0.013 | 0.112 |
警告
[1] 共分散行列は数値微分(複素ステップ)を使用して計算されました。
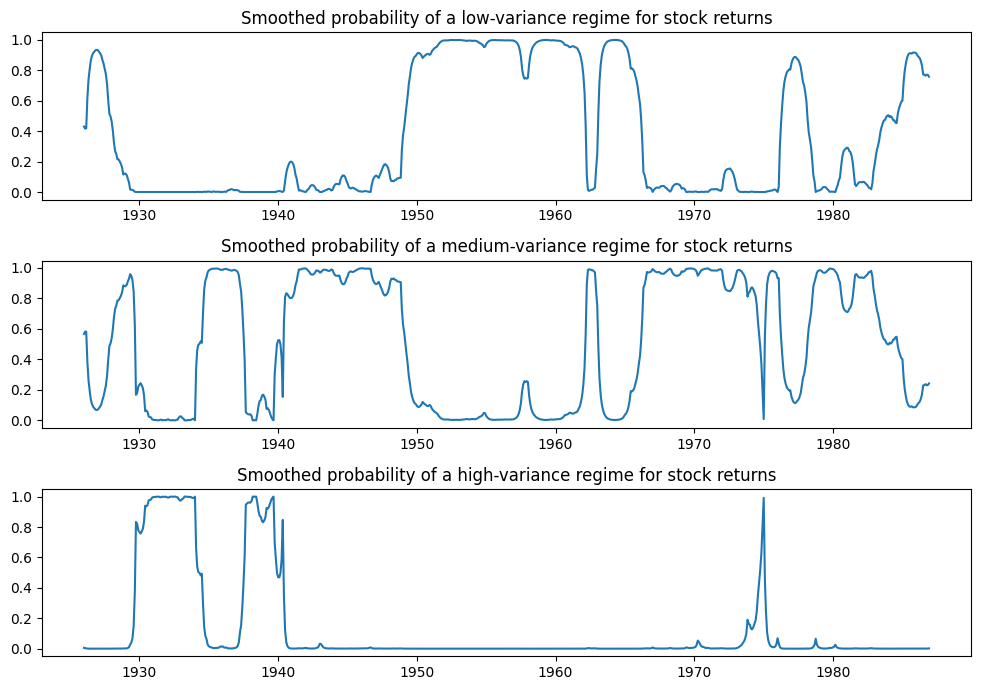
以下に、各レジームにある確率をプロットします。高分散レジームである可能性が高いのは、ごくわずかな期間のみです。
[8]:
fig, axes = plt.subplots(3, figsize=(10, 7))
ax = axes[0]
ax.plot(res_kns.smoothed_marginal_probabilities[0])
ax.set(title="Smoothed probability of a low-variance regime for stock returns")
ax = axes[1]
ax.plot(res_kns.smoothed_marginal_probabilities[1])
ax.set(title="Smoothed probability of a medium-variance regime for stock returns")
ax = axes[2]
ax.plot(res_kns.smoothed_marginal_probabilities[2])
ax.set(title="Smoothed probability of a high-variance regime for stock returns")
fig.tight_layout()
フィラルド(1994)時間変動遷移確率¶
このモデルは、時間変動遷移確率による推定を示します。データセットはhttp://econ.korea.ac.kr/~cjkim/MARKOV/data/filardo.prnで入手できます。
上記のモデルでは、遷移確率が時間を通じて一定であると仮定しました。ここでは、経済状況に応じて確率が変化することを許可します。それ以外の場合、モデルはハミルトン(1989)のマルコフ自己回帰モデルと同じです。
各期間において、レジームは、以下の時間変動遷移確率の行列に従って遷移します。
ここで、\(p_{ij,t}\)は、期間\(t\)において、レジーム\(i\)からレジーム\(j\)へ遷移する確率であり、以下のように定義されます。
遷移確率を最尤推定の一部として推定する代わりに、回帰係数\(\beta_{ij}\)が推定されます。これらの係数は、遷移確率を、事前決定されたまたは外生的な回帰変数\(x_{t-1}\)のベクトルに関連付けます。
[9]:
# Get the dataset
filardo = requests.get("http://econ.korea.ac.kr/~cjkim/MARKOV/data/filardo.prn").content
dta_filardo = pd.read_table(
BytesIO(filardo), sep=" +", header=None, skipfooter=1, engine="python"
)
dta_filardo.columns = ["month", "ip", "leading"]
dta_filardo.index = pd.date_range("1948-01-01", "1991-04-01", freq="MS")
dta_filardo["dlip"] = np.log(dta_filardo["ip"]).diff() * 100
# Deflated pre-1960 observations by ratio of std. devs.
# See hmt_tvp.opt or Filardo (1994) p. 302
std_ratio = (
dta_filardo["dlip"]["1960-01-01":].std() / dta_filardo["dlip"][:"1959-12-01"].std()
)
dta_filardo.loc[:"1959-12-01", "dlip"] = dta_filardo["dlip"][:"1959-12-01"] * std_ratio
dta_filardo["dlleading"] = np.log(dta_filardo["leading"]).diff() * 100
dta_filardo["dmdlleading"] = dta_filardo["dlleading"] - dta_filardo["dlleading"].mean()
# Plot the data
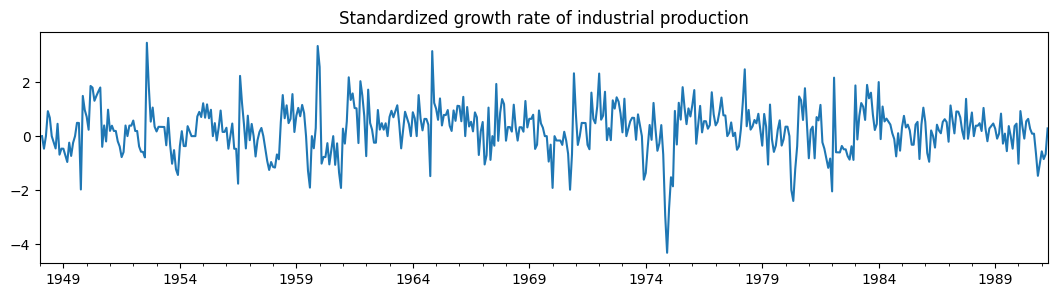
dta_filardo["dlip"].plot(
title="Standardized growth rate of industrial production", figsize=(13, 3)
)
plt.figure()
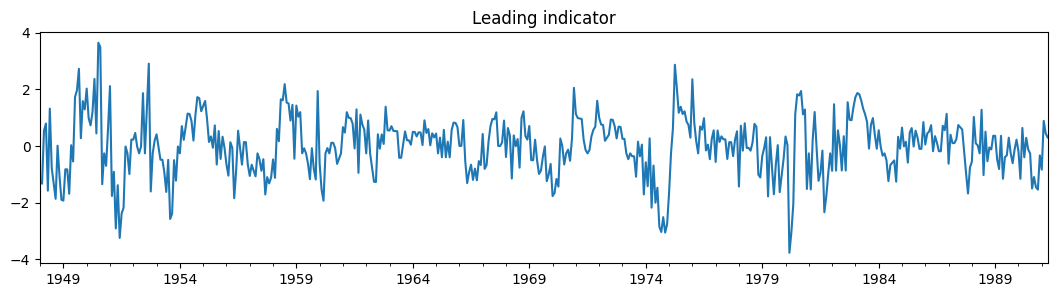
dta_filardo["dmdlleading"].plot(title="Leading indicator", figsize=(13, 3))
[9]:
<Axes: title={'center': 'Leading indicator'}>
時間変動遷移確率は、exog_tvtpパラメータで指定します。
ここでは、モデルフィッティングの別の機能、つまり、MLE初期パラメータのランダムサーチの使用を示します。マルコフスイッチングモデルは、尤度関数の多くの局所最大値によって特徴づけられることが多いため、初期の最適化ステップを実行すると、最適なパラメータを見つけるのに役立つ場合があります。
以下では、開始パラメータベクトルからの20個のランダムな摂動が調べられ、最適なものが実際の開始パラメータとして使用されることを指定します。検索のランダムな性質のため、結果を再現できるように、事前に乱数ジェネレーターにシードを設定します。
[10]:
mod_filardo = sm.tsa.MarkovAutoregression(
dta_filardo.iloc[2:]["dlip"],
k_regimes=2,
order=4,
switching_ar=False,
exog_tvtp=sm.add_constant(dta_filardo.iloc[1:-1]["dmdlleading"]),
)
np.random.seed(12345)
res_filardo = mod_filardo.fit(search_reps=20)
[11]:
res_filardo.summary()
[11]:
| 従属変数 | dlip | 観測数 | 514 |
|---|---|---|---|
| モデル | MarkovAutoregression | 対数尤度 | -586.572 |
| 日付 | 2024年10月3日(木) | AIC | 1195.144 |
| 時間 | 15:45:14 | BIC | 1241.808 |
| サンプル | 03-01-1948 | HQIC | 1213.433 |
| - 04-01-1991 | |||
| 共分散タイプ | 近似 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | -0.8659 | 0.153 | -5.658 | 0.000 | -1.166 | -0.566 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 0.5173 | 0.077 | 6.706 | 0.000 | 0.366 | 0.668 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| sigma2 | 0.4844 | 0.037 | 13.172 | 0.000 | 0.412 | 0.556 |
| ar.L1 | 0.1895 | 0.050 | 3.761 | 0.000 | 0.091 | 0.288 |
| ar.L2 | 0.0793 | 0.051 | 1.552 | 0.121 | -0.021 | 0.180 |
| ar.L3 | 0.1109 | 0.052 | 2.136 | 0.033 | 0.009 | 0.213 |
| ar.L4 | 0.1223 | 0.051 | 2.418 | 0.016 | 0.023 | 0.221 |
| coef | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| p[0->0].tvtp0 | 1.6494 | 0.446 | 3.702 | 0.000 | 0.776 | 2.523 |
| p[1->0].tvtp0 | -4.3595 | 0.747 | -5.833 | 0.000 | -5.824 | -2.895 |
| p[0->0].tvtp1 | -0.9945 | 0.566 | -1.758 | 0.079 | -2.103 | 0.114 |
| p[1->0].tvtp1 | -1.7702 | 0.508 | -3.484 | 0.000 | -2.766 | -0.775 |
警告
[1] 共分散行列は数値微分(複素ステップ)を使用して計算されました。
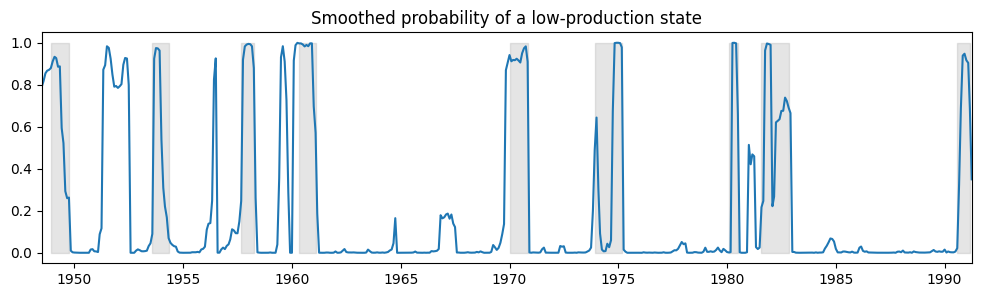
以下に、低生産状態で経済が稼働している平滑化された確率をプロットし、比較のためにNBERの景気後退を再度含めます。
[12]:
fig, ax = plt.subplots(figsize=(12, 3))
ax.plot(res_filardo.smoothed_marginal_probabilities[0])
ax.fill_between(usrec.index, 0, 1, where=usrec["USREC"].values, color="gray", alpha=0.2)
ax.set_xlim(dta_filardo.index[6], dta_filardo.index[-1])
ax.set(title="Smoothed probability of a low-production state")
[12]:
[Text(0.5, 1.0, 'Smoothed probability of a low-production state')]
時間変動遷移確率を使用して、低生産状態の予想される期間が時間の経過とともにどのように変化するかを確認できます。
[13]:
res_filardo.expected_durations[0].plot(
title="Expected duration of a low-production state", figsize=(12, 3)
)
[13]:
<Axes: title={'center': 'Expected duration of a low-production state'}>
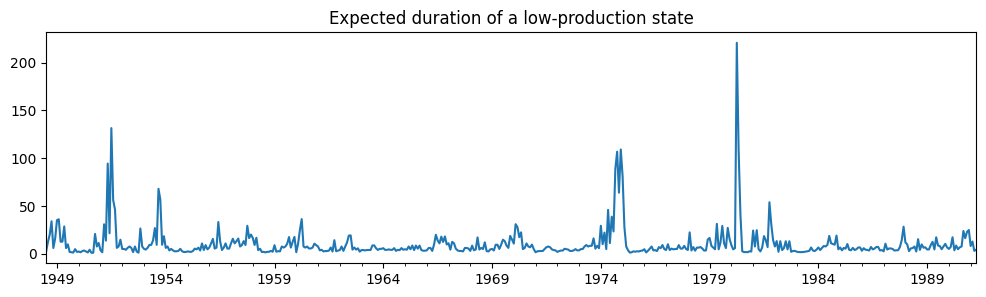
景気後退時には、低生産状態の予想される期間が景気拡大時よりも大幅に長くなります。