定常性とデトレンド (ADF/KPSS)¶

定常性とは、時系列の統計的特性、つまり平均、分散、共分散が時間とともに変化しないことを意味します。多くの統計モデルは、効果的で正確な予測を行うために、時系列が定常であることを必要とします。

時系列の定常性を確認するために、拡張ディッキー・フラー検定（Augmented Dickey Fuller test、「ADF」検定）とクワトコウスキー・フィリップス・シュミット・シン検定（Kwiatkowski-Phillips-Schmidt-Shin test、「KPSS」検定）の2つの統計検定が使用されます。非定常時系列を定常時系列に変換する方法も使用されます。

最初のセルでは、標準的なパッケージをインポートし、プロットをインラインで表示するように設定します。

[1]:

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm

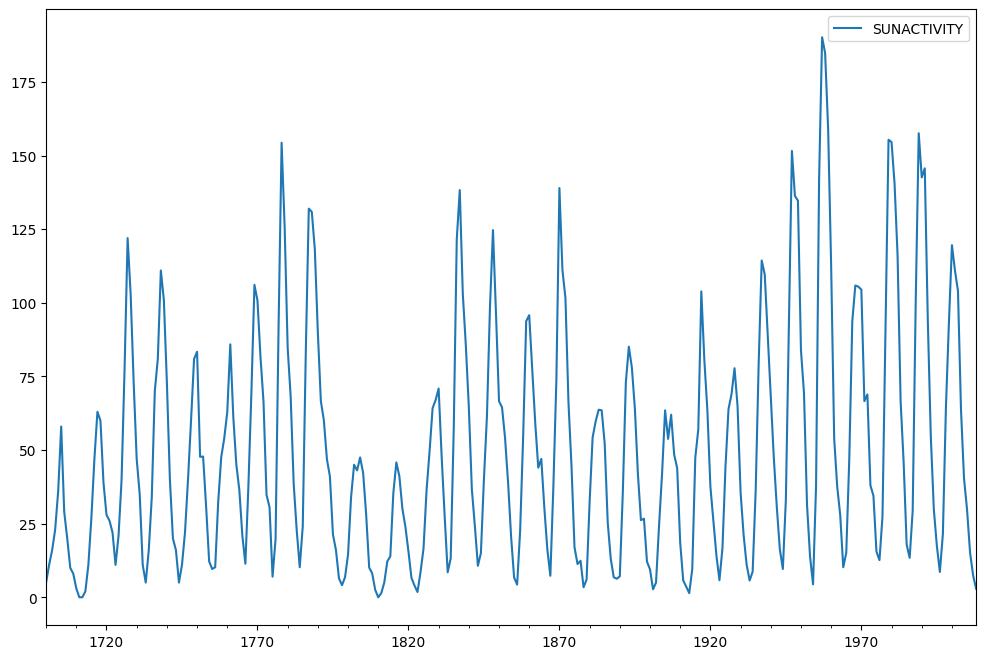
黒点データセットを使用します。これは、国立地球物理データセンターからの黒点に関する年間データ（1700～2008年）を含んでいます。

[2]:

sunspots = sm.datasets.sunspots.load_pandas().data

データに対していくつかの前処理が行われます。「YEAR」列はインデックスの作成に使用されます。

[3]:

sunspots.index = pd.Index(sm.tsa.datetools.dates_from_range("1700", "2008"))
del sunspots["YEAR"]

データがプロットされます。

[4]:

sunspots.plot(figsize=(12, 8))

[4]:

<Axes: >

ADF検定¶

ADF検定は、時系列における単位根の存在を判定するために使用され、それによって時系列が定常であるかどうかを理解するのに役立ちます。この検定の帰無仮説と対立仮説は次のとおりです。

帰無仮説：時系列は単位根を持つ。

対立仮説：時系列は単位根を持たない。

帰無仮説が棄却されなかった場合、この検定は時系列が非定常であるという証拠を提供する可能性があります。

時系列に対してADF検定を実行する関数が作成されます。

[5]:

from statsmodels.tsa.stattools import adfuller


def adf_test(timeseries):
    print("Results of Dickey-Fuller Test:")
    dftest = adfuller(timeseries, autolag="AIC")
    dfoutput = pd.Series(
        dftest[0:4],
        index=[
            "Test Statistic",
            "p-value",
            "#Lags Used",
            "Number of Observations Used",
        ],
    )
    for key, value in dftest[4].items():
        dfoutput["Critical Value (%s)" % key] = value
    print(dfoutput)

KPSS検定¶

KPSS検定は、時系列の定常性を確認するための別の検定です。KPSS検定の帰無仮説と対立仮説は、ADF検定とは逆です。

帰無仮説：過程はトレンド定常である。

対立仮説：時系列は単位根を持つ（時系列は定常ではない）。

時系列に対してKPSS検定を実行する関数が作成されます。

[6]:

from statsmodels.tsa.stattools import kpss


def kpss_test(timeseries):
    print("Results of KPSS Test:")
    kpsstest = kpss(timeseries, regression="c", nlags="auto")
    kpss_output = pd.Series(
        kpsstest[0:3], index=["Test Statistic", "p-value", "Lags Used"]
    )
    for key, value in kpsstest[3].items():
        kpss_output["Critical Value (%s)" % key] = value
    print(kpss_output)

ADF検定は、次の結果を返します。検定統計量、p値、1％、5％、10％信頼区間の臨界値。

データにADF検定が適用されます。

[7]:

adf_test(sunspots["SUNACTIVITY"])

Results of Dickey-Fuller Test:
Test Statistic                  -2.837781
p-value                          0.053076
#Lags Used                       8.000000
Number of Observations Used    300.000000
Critical Value (1%)             -3.452337
Critical Value (5%)             -2.871223
Critical Value (10%)            -2.571929
dtype: float64

有意水準0.05とADF検定のp値に基づいて、帰無仮説は棄却できません。したがって、時系列は非定常です。

KPSS検定は、次の結果を返します。検定統計量、p値、1％、5％、10％信頼区間の臨界値。

データにKPSS検定が適用されます。

[8]:

kpss_test(sunspots["SUNACTIVITY"])

Results of KPSS Test:
Test Statistic           0.669866
p-value                  0.016285
Lags Used                7.000000
Critical Value (10%)     0.347000
Critical Value (5%)      0.463000
Critical Value (2.5%)    0.574000
Critical Value (1%)      0.739000
dtype: float64

有意水準0.05とKPSS検定のp値に基づいて、対立仮説を支持して帰無仮説を棄却する証拠があります。したがって、KPSS検定によると、時系列は非定常です。

時系列が真に定常であることを確認するために、常に両方の検定を適用することが最善です。これらの定常性検定を適用した可能性のある結果は次のとおりです。

ここでは、ADF検定とKPSS検定の結果に違いがあるため、時系列はトレンド定常であり、厳密に定常ではないと推測できます。時系列は、差分またはモデルフィッティングによってデトレンドできます。

差分によるデトレンド¶

これは、時系列をデトレンドするための最も簡単な方法の1つです。現在のタイムステップの値は、元の観測値と前のタイムステップの観測値の差として計算される新しい時系列が構築されます。

差分がデータに適用され、その結果がプロットされます。

[9]:

sunspots["SUNACTIVITY_diff"] = sunspots["SUNACTIVITY"] - sunspots["SUNACTIVITY"].shift(
    1
)
sunspots["SUNACTIVITY_diff"].dropna().plot(figsize=(12, 8))

[9]:

<Axes: >

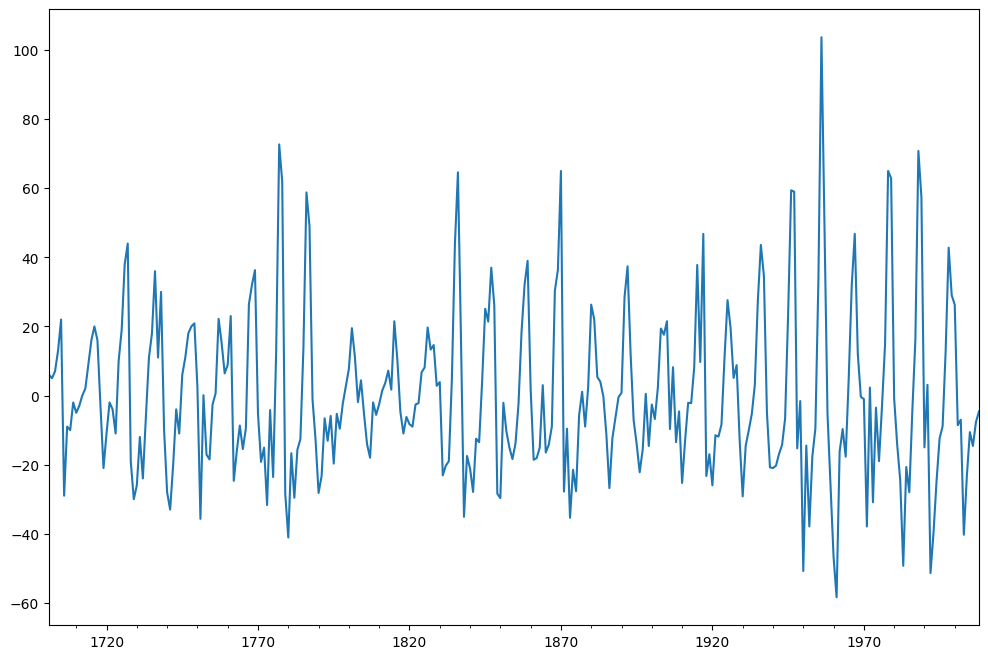
これらのデトレンドされた値にADF検定が適用され、定常性が確認されます。

[10]:

adf_test(sunspots["SUNACTIVITY_diff"].dropna())

Results of Dickey-Fuller Test:
Test Statistic                -1.486166e+01
p-value                        1.715552e-27
#Lags Used                     7.000000e+00
Number of Observations Used    3.000000e+02
Critical Value (1%)           -3.452337e+00
Critical Value (5%)           -2.871223e+00
Critical Value (10%)          -2.571929e+00
dtype: float64

ADF検定のp値に基づいて、対立仮説を支持して帰無仮説を棄却する証拠があります。したがって、時系列は現在厳密に定常です。

これらのデトレンドされた値にKPSS検定が適用され、定常性が確認されます。

[11]:

kpss_test(sunspots["SUNACTIVITY_diff"].dropna())

Results of KPSS Test:
Test Statistic           0.021193
p-value                  0.100000
Lags Used                0.000000
Critical Value (10%)     0.347000
Critical Value (5%)      0.463000
Critical Value (2.5%)    0.574000
Critical Value (1%)      0.739000
dtype: float64

/tmp/ipykernel_4050/1512460390.py:6: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.

  kpsstest = kpss(timeseries, regression="c", nlags="auto")

KPSS検定のp値に基づいて、帰無仮説は棄却できません。したがって、時系列は定常です。

結論¶

時系列の定常性を確認するための2つの検定、つまりADF検定とKPSS検定が使用されます。デトレンドは差分を使用して実行されます。トレンド定常時系列は厳密に定常な時系列に変換されます。必要な予測モデルを定常時系列データに適用できるようになりました。