マルコフスイッチング動的回帰モデル¶

このノートブックでは、statsmodelsでマルコフスイッチングモデルを使用して、レジームの変化を伴う動的回帰モデルを推定する例を示します。これは、Stataのマルコフスイッチングドキュメントの例に従っており、http://www.stata.com/manuals14/tsmswitch.pdfにあります。

[1]:

%matplotlib inline

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

# NBER recessions
from pandas_datareader.data import DataReader
from datetime import datetime

usrec = DataReader(
    "USREC", "fred", start=datetime(1947, 1, 1), end=datetime(2013, 4, 1)
)

切片が切り替わるフェデラルファンド金利¶

最初の例では、フェデラルファンド金利を、一定の切片を中心としたノイズとしてモデル化しますが、切片は異なるレジーム中に変化します。モデルは単純に

\[r_t = \mu_{S_t} + \varepsilon_t \qquad \varepsilon_t \sim N(0, \sigma^2)\]

ここで、\(S_t \in \{0, 1\}\)であり、レジーム遷移は次のように行われます。

\[\begin{split} P(S_t = s_t | S_{t-1} = s_{t-1}) = \begin{bmatrix} p_{00} & p_{10} \\ 1 - p_{00} & 1 - p_{10} \end{bmatrix}\end{split}\]

このモデルのパラメータを最尤法で推定します: \(p_{00}, p_{10}, \mu_0, \mu_1, \sigma^2\).

この例で使用されているデータは、https://www.stata-press.com/data/r14/usmacroにあります。

[2]:

# Get the federal funds rate data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import fedfunds

dta_fedfunds = pd.Series(
    fedfunds, index=pd.date_range("1954-07-01", "2010-10-01", freq="QS")
)

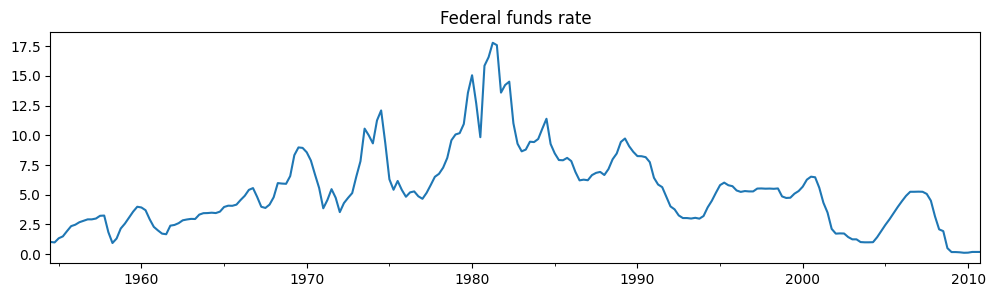
# Plot the data
dta_fedfunds.plot(title="Federal funds rate", figsize=(12, 3))

# Fit the model
# (a switching mean is the default of the MarkovRegession model)
mod_fedfunds = sm.tsa.MarkovRegression(dta_fedfunds, k_regimes=2)
res_fedfunds = mod_fedfunds.fit()

../../../_images/examples_notebooks_generated_markov_regression_4_0.png

[3]:

res_fedfunds.summary()

[3]:

マルコフスイッチングモデルの結果
従属変数	y	観測値の数	226
モデル	MarkovRegression	対数尤度	-508.636
日付	2024年10月3日(木)	AIC	1027.272
時間	15:45:37	BIC	1044.375
サンプル	07-01-1954	HQIC	1034.174
	- 10-01-2010
共分散型	近似

レジーム0のパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
const	3.7088	0.177	20.988	0.000	3.362	4.055

レジーム1のパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
const	9.5568	0.300	31.857	0.000	8.969	10.145

非スイッチングパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
sigma2	4.4418	0.425	10.447	0.000	3.608	5.275

レジーム遷移パラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
p[0->0]	0.9821	0.010	94.443	0.000	0.962	1.002
p[1->0]	0.0504	0.027	1.876	0.061	-0.002	0.103

警告
[1] 共分散行列は、数値（複素数ステップ）微分を使用して計算されました。

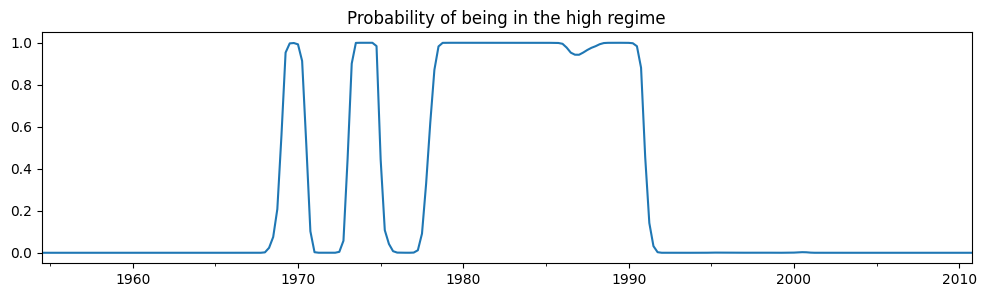
要約出力から、最初のレジーム（「低レジーム」）におけるフェデラルファンド金利の平均は\(3.7\)と推定され、「高レジーム」では\(9.6\)と推定されます。以下に、高レジームであることのスムージングされた確率をプロットします。このモデルは、1980年代が高フェデラルファンド金利が存在した時代であったことを示唆しています。

[4]:

res_fedfunds.smoothed_marginal_probabilities[1].plot(
    title="Probability of being in the high regime", figsize=(12, 3)
)

[4]:

<Axes: title={'center': 'Probability of being in the high regime'}>

../../../_images/examples_notebooks_generated_markov_regression_7_1.png

推定された遷移行列から、低レジームと高レジームのそれぞれの期待持続時間を計算できます。

[5]:

print(res_fedfunds.expected_durations)

[55.85400626 19.85506546]

低レジームは約14年間持続すると予想されるのに対し、高レジームは約5年間しか持続しないと予想されます。

切片とラグ付き従属変数が切り替わるフェデラルファンド金利¶

2番目の例では、前回のモデルを拡張して、フェデラルファンド金利のラグ付き値を含めます。

\[r_t = \mu_{S_t} + r_{t-1} \beta_{S_t} + \varepsilon_t \qquad \varepsilon_t \sim N(0, \sigma^2)\]

ここで、\(S_t \in \{0, 1\}\)であり、レジーム遷移は次のように行われます。

\[\begin{split} P(S_t = s_t | S_{t-1} = s_{t-1}) = \begin{bmatrix} p_{00} & p_{10} \\ 1 - p_{00} & 1 - p_{10} \end{bmatrix}\end{split}\]

このモデルのパラメータを最尤法で推定します: \(p_{00}, p_{10}, \mu_0, \mu_1, \beta_0, \beta_1, \sigma^2\).

[6]:

# Fit the model
mod_fedfunds2 = sm.tsa.MarkovRegression(
    dta_fedfunds.iloc[1:], k_regimes=2, exog=dta_fedfunds.iloc[:-1]
)
res_fedfunds2 = mod_fedfunds2.fit()

[7]:

res_fedfunds2.summary()

[7]:

マルコフスイッチングモデルの結果
従属変数	y	観測値の数	225
モデル	MarkovRegression	対数尤度	-264.711
日付	2024年10月3日(木)	AIC	543.421
時間	15:45:38	BIC	567.334
サンプル	10-01-1954	HQIC	553.073
	- 10-01-2010
共分散型	近似

レジーム0のパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
const	0.7245	0.289	2.510	0.012	0.159	1.290
x1	0.7631	0.034	22.629	0.000	0.697	0.829

レジーム1のパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
const	-0.0989	0.118	-0.835	0.404	-0.331	0.133
x1	1.0612	0.019	57.351	0.000	1.025	1.097

非スイッチングパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
sigma2	0.4783	0.050	9.642	0.000	0.381	0.576

レジーム遷移パラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
p[0->0]	0.6378	0.120	5.304	0.000	0.402	0.874
p[1->0]	0.1306	0.050	2.634	0.008	0.033	0.228

警告
[1] 共分散行列は、数値（複素数ステップ）微分を使用して計算されました。

要約出力からいくつか注目すべき点があります。

情報基準が大幅に低下しており、このモデルが前のモデルよりも適合度が高いことを示しています。
切片の観点から、レジームの解釈が切り替わりました。現在、最初のレジームがより高い切片を持ち、2番目のレジームがより低い切片を持っています。

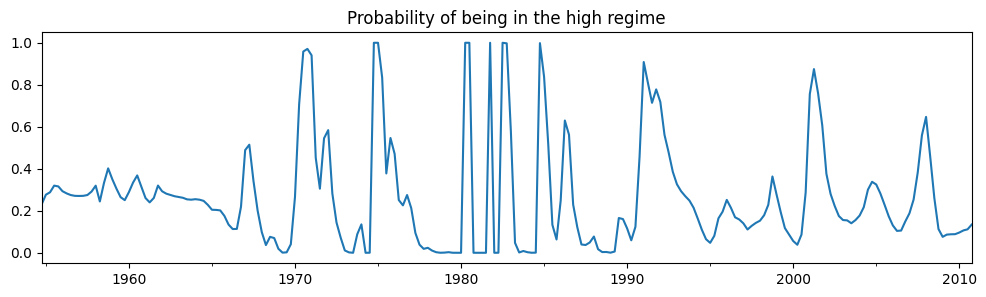
高レジーム状態のスムージングされた確率を調べると、かなりの変動が見られます。

[8]:

res_fedfunds2.smoothed_marginal_probabilities[0].plot(
    title="Probability of being in the high regime", figsize=(12, 3)
)

[8]:

<Axes: title={'center': 'Probability of being in the high regime'}>

../../../_images/examples_notebooks_generated_markov_regression_15_1.png

最後に、各レジームの予想持続時間がかなり短縮されました。

[9]:

print(res_fedfunds2.expected_durations)

[2.76105188 7.65529154]

2つまたは3つのレジームを持つテーラールール¶

ここで、出力ギャップの尺度とインフレの尺度という2つの追加の外生変数を含め、2つと3つの両方のレジームを持つスイッチングテーラー型ルールを推定し、どちらがデータによく適合するかを確認します。

モデルは推定が難しいことが多いため、3レジームモデルでは、結果を改善するために開始パラメータに対する検索を使用し、20回のランダム検索の繰り返しを指定します。

[10]:

# Get the additional data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import ogap, inf

dta_ogap = pd.Series(ogap, index=pd.date_range("1954-07-01", "2010-10-01", freq="QS"))
dta_inf = pd.Series(inf, index=pd.date_range("1954-07-01", "2010-10-01", freq="QS"))

exog = pd.concat((dta_fedfunds.shift(), dta_ogap, dta_inf), axis=1).iloc[4:]

# Fit the 2-regime model
mod_fedfunds3 = sm.tsa.MarkovRegression(dta_fedfunds.iloc[4:], k_regimes=2, exog=exog)
res_fedfunds3 = mod_fedfunds3.fit()

# Fit the 3-regime model
np.random.seed(12345)
mod_fedfunds4 = sm.tsa.MarkovRegression(dta_fedfunds.iloc[4:], k_regimes=3, exog=exog)
res_fedfunds4 = mod_fedfunds4.fit(search_reps=20)

[11]:

res_fedfunds3.summary()

[11]:

マルコフスイッチングモデルの結果
従属変数	y	観測値の数	222
モデル	MarkovRegression	対数尤度	-229.256
日付	2024年10月3日(木)	AIC	480.512
時間	15:45:42	BIC	517.942
サンプル	07-01-1955	HQIC	495.624
	- 10-01-2010
共分散型	近似

レジーム0のパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
const	0.6555	0.137	4.771	0.000	0.386	0.925
x1	0.8314	0.033	24.951	0.000	0.766	0.897
x2	0.1355	0.029	4.609	0.000	0.078	0.193
x3	-0.0274	0.041	-0.671	0.502	-0.107	0.053

レジーム1のパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
const	-0.0945	0.128	-0.739	0.460	-0.345	0.156
x1	0.9293	0.027	34.309	0.000	0.876	0.982
x2	0.0343	0.024	1.429	0.153	-0.013	0.081
x3	0.2125	0.030	7.147	0.000	0.154	0.271

非スイッチングパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
sigma2	0.3323	0.035	9.526	0.000	0.264	0.401

レジーム遷移パラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
p[0->0]	0.7279	0.093	7.828	0.000	0.546	0.910
p[1->0]	0.2115	0.064	3.298	0.001	0.086	0.337

警告
[1] 共分散行列は、数値（複素数ステップ）微分を使用して計算されました。

[12]:

res_fedfunds4.summary()

[12]:

マルコフスイッチングモデルの結果
従属変数	y	観測値の数	222
モデル	MarkovRegression	対数尤度	-180.806
日付	2024年10月3日(木)	AIC	399.611
時間	15:45:42	BIC	464.262
サンプル	07-01-1955	HQIC	425.713
	- 10-01-2010
共分散型	近似

レジーム0のパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
const	-1.0250	0.290	-3.531	0.000	-1.594	-0.456
x1	0.3277	0.086	3.812	0.000	0.159	0.496
x2	0.2036	0.049	4.152	0.000	0.107	0.300
x3	1.1381	0.081	13.977	0.000	0.978	1.298

レジーム1のパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
const	-0.0259	0.087	-0.298	0.765	-0.196	0.144
x1	0.9737	0.019	50.265	0.000	0.936	1.012
x2	0.0341	0.017	2.030	0.042	0.001	0.067
x3	0.1215	0.022	5.606	0.000	0.079	0.164

レジーム2のパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
const	0.7346	0.130	5.632	0.000	0.479	0.990
x1	0.8436	0.024	35.198	0.000	0.797	0.891
x2	0.1633	0.025	6.515	0.000	0.114	0.212
x3	-0.0499	0.027	-1.835	0.067	-0.103	0.003

非スイッチングパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
sigma2	0.1660	0.018	9.240	0.000	0.131	0.201

レジーム遷移パラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
p[0->0]	0.7214	0.117	6.177	0.000	0.493	0.950
p[1->0]	4.001e-08	nan	nan	nan	nan	nan
p[2->0]	0.0783	0.038	2.079	0.038	0.004	0.152
p[0->1]	0.1044	0.095	1.103	0.270	-0.081	0.290
p[1->1]	0.8259	0.054	15.208	0.000	0.719	0.932
p[2->1]	0.2288	0.073	3.150	0.002	0.086	0.371

警告
[1] 共分散行列は、数値（複素数ステップ）微分を使用して計算されました。

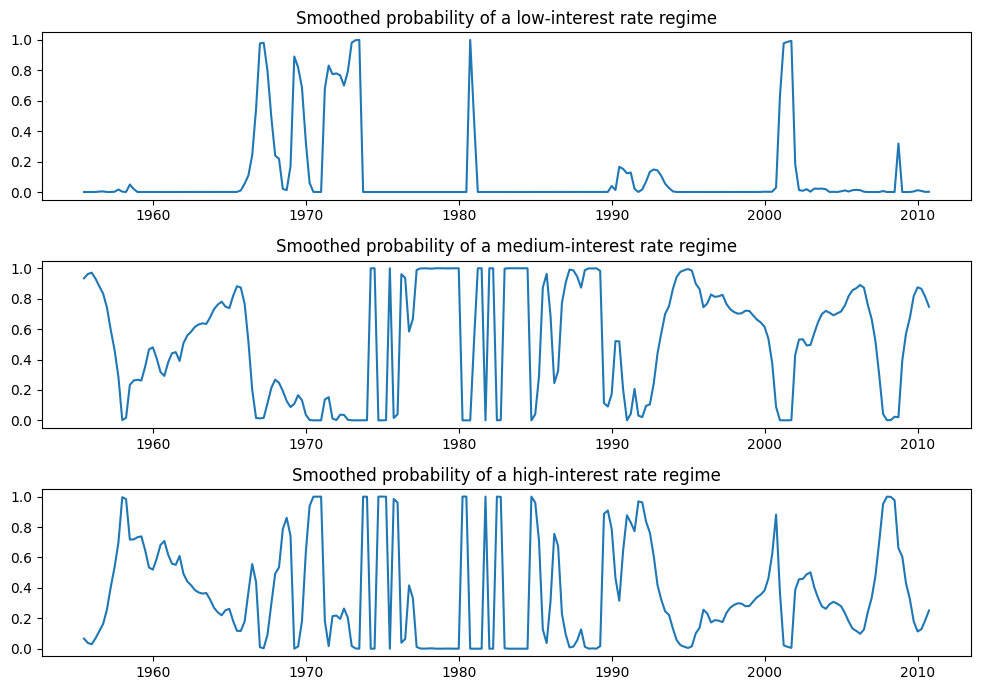
情報基準が低いため、低、中、高金利レジームの解釈で、3状態モデルを優先する可能性があります。各レジームのスムージングされた確率を以下にプロットします。

[13]:

fig, axes = plt.subplots(3, figsize=(10, 7))

ax = axes[0]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[0])
ax.set(title="Smoothed probability of a low-interest rate regime")

ax = axes[1]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[1])
ax.set(title="Smoothed probability of a medium-interest rate regime")

ax = axes[2]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[2])
ax.set(title="Smoothed probability of a high-interest rate regime")

fig.tight_layout()

../../../_images/examples_notebooks_generated_markov_regression_23_0.png

切り替え分散¶

切り替え分散にも対応できます。特に、次のモデルを検討します。

\[y_t = \mu_{S_t} + y_{t-1} \beta_{S_t} + \varepsilon_t \quad \varepsilon_t \sim N(0, \sigma_{S_t}^2)\]

このモデルのパラメータを最尤法で推定します: \(p_{00}, p_{10}, \mu_0, \mu_1, \beta_0, \beta_1, \sigma_0^2, \sigma_1^2\).

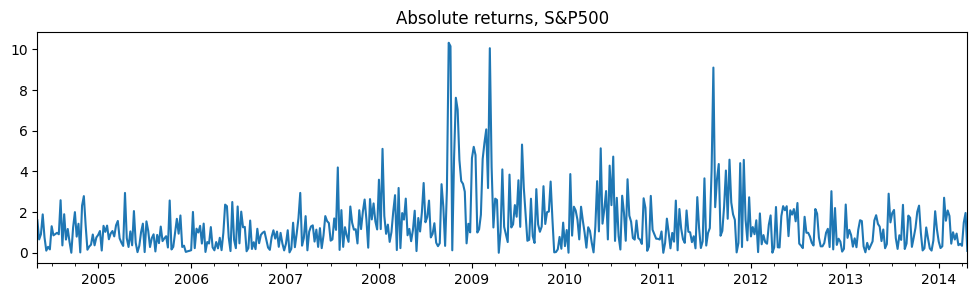
このアプリケーションは、株式の絶対収益であり、データはhttps://www.stata-press.com/data/r14/snp500にあります。

[14]:

# Get the federal funds rate data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import areturns

dta_areturns = pd.Series(
    areturns, index=pd.date_range("2004-05-04", "2014-5-03", freq="W")
)

# Plot the data
dta_areturns.plot(title="Absolute returns, S&P500", figsize=(12, 3))

# Fit the model
mod_areturns = sm.tsa.MarkovRegression(
    dta_areturns.iloc[1:],
    k_regimes=2,
    exog=dta_areturns.iloc[:-1],
    switching_variance=True,
)
res_areturns = mod_areturns.fit()

../../../_images/examples_notebooks_generated_markov_regression_25_0.png

[15]:

res_areturns.summary()

[15]:

マルコフスイッチングモデルの結果
従属変数	y	観測値の数	520
モデル	MarkovRegression	対数尤度	-745.798
日付	2024年10月3日(木)	AIC	1507.595
時間	15:45:44	BIC	1541.626
サンプル	05-16-2004	HQIC	1520.926
	- 04-27-2014
共分散型	近似

レジーム0のパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
const	0.7641	0.078	9.761	0.000	0.611	0.918
x1	0.0791	0.030	2.620	0.009	0.020	0.138
sigma2	0.3476	0.061	5.694	0.000	0.228	0.467

レジーム1のパラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
const	1.9728	0.278	7.086	0.000	1.427	2.518
x1	0.5280	0.086	6.155	0.000	0.360	0.696
sigma2	2.5771	0.405	6.357	0.000	1.783	3.372

レジーム遷移パラメータ
	coef	標準誤差	z	P>\|z\|	[0.025	0.975]
p[0->0]	0.7531	0.063	11.871	0.000	0.629	0.877
p[1->0]	0.6825	0.066	10.301	0.000	0.553	0.812

警告
[1] 共分散行列は、数値（複素数ステップ）微分を使用して計算されました。

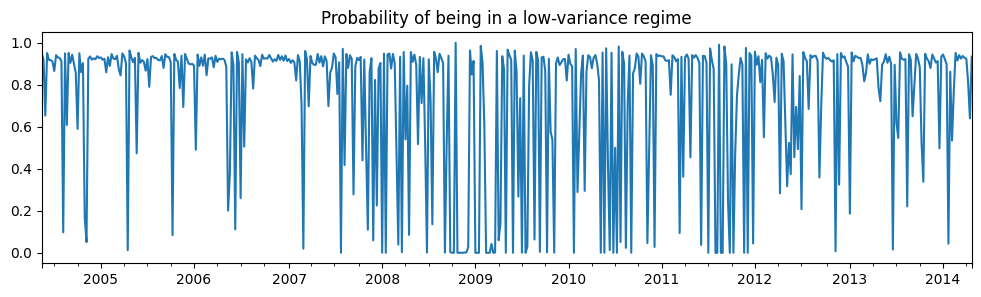
最初のレジームは低分散レジームであり、2番目のレジームは高分散レジームです。以下に、低分散レジームにある確率をプロットします。2008年から2012年の間には、経済を主導する1つのレジームの明確な兆候はないようです。

[16]:

res_areturns.smoothed_marginal_probabilities[0].plot(
    title="Probability of being in a low-variance regime", figsize=(12, 3)
)

[16]:

<Axes: title={'center': 'Probability of being in a low-variance regime'}>

../../../_images/examples_notebooks_generated_markov_regression_28_1.png

最終更新日: 2024年10月3日