動的因子と一致指数¶
因子モデルは、一般的に、多数の観測変数の変動のかなりの部分を左右する少数の未観測の「因子」を見つけようとするもので、主成分分析などの次元削減手法と関連しています。動的因子モデルは、未観測因子の遷移ダイナミクスを明示的にモデル化するため、時系列データによく適用されます。
マクロ経済の一致指数は、「景気循環」の共通成分を捉えるように設計されています。このような成分は、多くのマクロ経済変数に同時に影響を与えると想定されています。一致指数(例えば、一致経済指標)の推定と使用は動的因子モデルよりも前から行われていましたが、Stock and Watson(1989、1991)は、いくつかの影響力のある論文で動的因子モデルを使用して、それらの理論的基礎を提供しました。
以下では、Kim and Nelson(1999)によるStock and Watson(1991)モデルの扱いに従って、動的因子モデルを定式化し、最尤法によってパラメータを推定し、一致指数を作成します。
マクロ経済データ¶
一致指数は、4つのマクロ経済変数の共変動を考慮することによって作成されます(これらの変数のバージョンはFREDで入手できます。以下で使用される系列のIDは括弧内に示されています)。
工業生産(IPMAN)
実質総所得(移転支払いを除く)(W875RX1)
製造業・貿易販売(CMRMTSPL)
非農業部門雇用者数(PAYEMS)
いずれの場合も、データは月次頻度で、季節調整済みです。考慮される期間は1972年から2005年です。
[1]:
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
np.set_printoptions(precision=4, suppress=True, linewidth=120)
[2]:
from pandas_datareader.data import DataReader
# Get the datasets from FRED
start = '1979-01-01'
end = '2014-12-01'
indprod = DataReader('IPMAN', 'fred', start=start, end=end)
income = DataReader('W875RX1', 'fred', start=start, end=end)
sales = DataReader('CMRMTSPL', 'fred', start=start, end=end)
emp = DataReader('PAYEMS', 'fred', start=start, end=end)
# dta = pd.concat((indprod, income, sales, emp), axis=1)
# dta.columns = ['indprod', 'income', 'sales', 'emp']
**注**:FREDの最近の更新(2015年8月12日)で、時系列CMRMTSPLは1997年から始まるように切り詰められました。これは、CMRMTSPLがスプライスされた系列であるため、おそらく誤りです。初期の期間は系列HMRMTからのもので、後期の期間はCMRMTによって定義されています。
これはその後(2016年2月11日)修正されましたが、以下に示すように、HMRMTとCMRMTから手動で系列を構築することもできます(Alfred xlsファイルのノートから取得したプロセス)。
[3]:
# HMRMT = DataReader('HMRMT', 'fred', start='1967-01-01', end=end)
# CMRMT = DataReader('CMRMT', 'fred', start='1997-01-01', end=end)
[4]:
# HMRMT_growth = HMRMT.diff() / HMRMT.shift()
# sales = pd.Series(np.zeros(emp.shape[0]), index=emp.index)
# # Fill in the recent entries (1997 onwards)
# sales[CMRMT.index] = CMRMT
# # Backfill the previous entries (pre 1997)
# idx = sales.loc[:'1997-01-01'].index
# for t in range(len(idx)-1, 0, -1):
# month = idx[t]
# prev_month = idx[t-1]
# sales.loc[prev_month] = sales.loc[month] / (1 + HMRMT_growth.loc[prev_month].values)
[5]:
dta = pd.concat((indprod, income, sales, emp), axis=1)
dta.columns = ['indprod', 'income', 'sales', 'emp']
dta.index.freq = dta.index.inferred_freq
[6]:
dta.loc[:, 'indprod':'emp'].plot(subplots=True, layout=(2, 2), figsize=(15, 6));
Stock and Watson(1991)は、彼らのデータセットでは、各系列の単位根の帰無仮説を棄却できなかった(したがって、系列は統合されている)と報告していますが、系列が共和分されているという強い証拠は見つかりませんでした。
その結果、彼らは、平均値を引いて標準化した変数の一次階差(対数)を使用してモデルを推定することを提案しています。
[7]:
# Create log-differenced series
dta['dln_indprod'] = (np.log(dta.indprod)).diff() * 100
dta['dln_income'] = (np.log(dta.income)).diff() * 100
dta['dln_sales'] = (np.log(dta.sales)).diff() * 100
dta['dln_emp'] = (np.log(dta.emp)).diff() * 100
# De-mean and standardize
dta['std_indprod'] = (dta['dln_indprod'] - dta['dln_indprod'].mean()) / dta['dln_indprod'].std()
dta['std_income'] = (dta['dln_income'] - dta['dln_income'].mean()) / dta['dln_income'].std()
dta['std_sales'] = (dta['dln_sales'] - dta['dln_sales'].mean()) / dta['dln_sales'].std()
dta['std_emp'] = (dta['dln_emp'] - dta['dln_emp'].mean()) / dta['dln_emp'].std()
動的因子¶
一般的な動的因子モデルは次のように記述されます。
ここで、\(y_t\)は観測データ、\(f_t\)は未観測の因子(ベクトル自己回帰として進化)、\(x_t\)は(オプションの)外生変数、\(u_t\)は誤差または「特異的」プロセスです(\(u_t\)もオプションで自己相関を持つことができます)。\(\Lambda\)行列は、しばしば「因子負荷量」の行列と呼ばれます。因子誤差項の分散は、未観測因子の識別を確実にするために、単位行列に設定されます。
このモデルは状態空間形式にキャストでき、未観測因子はカルマンフィルターによって推定できます。尤度はフィルタリングの再帰の副産物として評価でき、最尤推定を使用してパラメータを推定できます。
モデルの仕様¶
このアプリケーションの特定の動的因子モデルには、AR(2)プロセスに従うと仮定される1つの未観測因子があります。イノベーション\(\varepsilon_t\)は独立していると仮定され(そのため、\(\Sigma\)は対角行列です)、各方程式に関連付けられた誤差項\(u_{i,t}\)は、独立したAR(2)プロセスに従うと仮定されます。
したがって、ここで考慮される仕様は次のとおりです。
ここで、\(i\)は次のいずれかです:[indprod, income, sales, emp ].
このモデルは、statsmodelsに組み込まれているDynamicFactorモデルを使用して定式化できます。具体的には、次の仕様があります。
k_factors = 1- (未観測因子は1つです)factor_order = 2- (AR(2)プロセスに従います)error_var = False- (誤差はVARとして共同で進化するのではなく、独立したARプロセスとして進化します - これはデフォルトオプションであるため、以下では指定されていません)error_order = 2- (誤差は次数2の自己相関があります。つまり、AR(2)プロセスです)error_cov_type = 'diagonal'- (イノベーションは無相関です。これもデフォルトです)
モデルが作成されると、パラメータは最尤法によって推定できます。これはfit()メソッドを使用して行われます.
**注**:データの平均値を引いて標準化したことを思い出してください。これは、以下の結果を解釈する上で重要になります。
**補足**:Kim and Nelson(1999)は、彼らの実証例では、雇用変数が因子の遅延値にも依存することを許可するわずかに異なるモデルを実際に検討しています。このモデルは組み込みのDynamicFactorクラスには適合しませんが、必要な新しいパラメータと制約を実装するためにサブクラスを使用することで対応できます。以下の付録Aを参照してください。
パラメータ推定¶
多変量モデルは比較的多数のパラメータを持つことができ、局所的な最小値から脱出して尤度を最大化するのが難しい場合があります。この問題を軽減するために、Scipyで利用可能な修正Powellメソッドを使用して、初期の最大化ステップ(モデル定義の開始パラメータから)を実行します(詳細については、最小化のドキュメントを参照してください)。結果のパラメータは、標準のLBFGS最適化メソッドの開始パラメータとして使用されます。
[8]:
# Get the endogenous data
endog = dta.loc['1979-02-01':, 'std_indprod':'std_emp']
# Create the model
mod = sm.tsa.DynamicFactor(endog, k_factors=1, factor_order=2, error_order=2)
initial_res = mod.fit(method='powell', disp=False)
res = mod.fit(initial_res.params, disp=False)
推定値¶
モデルが推定されると、分析または推論に使用できる2つのコンポーネントがあります。
推定されたパラメータ
推定された因子
パラメータ¶
推定されたパラメータは、モデルの意味を理解するのに役立ちますが、多数の観測変数や未観測因子を持つモデルでは、解釈が難しい場合があります。
この困難の1つの理由は、因子負荷量と未観測因子間の識別問題によるものです。容易にわかる識別問題の1つは、負荷量と因子の符号です。以下に示すモデルと同等のモデルは、すべての因子負荷量と未観測因子の符号を反転させることによって得られます。
ここで、このモデルで解釈しやすい意味の1つは、未観測因子の持続性です。かなりの持続性を示していることがわかりました。
[9]:
print(res.summary(separate_params=False))
Statespace Model Results
=================================================================================================================
Dep. Variable: ['std_indprod', 'std_income', 'std_sales', 'std_emp'] No. Observations: 431
Model: DynamicFactor(factors=1, order=2) Log Likelihood -1586.566
+ AR(2) errors AIC 3209.133
Date: Thu, 03 Oct 2024 BIC 3282.323
Time: 16:05:06 HQIC 3238.031
Sample: 02-01-1979
- 12-01-2014
Covariance Type: opg
====================================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------------------------
loading.f1.std_indprod 0.5044 0.007 70.635 0.000 0.490 0.518
loading.f1.std_income 0.2313 0.021 10.956 0.000 0.190 0.273
loading.f1.std_sales 0.2707 0.020 13.249 0.000 0.231 0.311
loading.f1.std_emp 0.6354 0.011 56.890 0.000 0.613 0.657
sigma2.std_indprod 0.0023 3.89e-05 59.178 0.000 0.002 0.002
sigma2.std_income 0.8423 0.022 37.629 0.000 0.798 0.886
sigma2.std_sales 0.7672 0.053 14.516 0.000 0.664 0.871
sigma2.std_emp 0.0553 0.001 91.451 0.000 0.054 0.056
L1.f1.f1 0.3455 0.024 14.605 0.000 0.299 0.392
L2.f1.f1 0.4471 0.025 17.718 0.000 0.398 0.497
L1.e(std_indprod).e(std_indprod) -1.9726 0.001 -3312.592 0.000 -1.974 -1.971
L2.e(std_indprod).e(std_indprod) -1.0000 2.82e-06 -3.54e+05 0.000 -1.000 -1.000
L1.e(std_income).e(std_income) -0.2412 0.019 -12.760 0.000 -0.278 -0.204
L2.e(std_income).e(std_income) -0.1400 0.033 -4.202 0.000 -0.205 -0.075
L1.e(std_sales).e(std_sales) -0.3118 0.043 -7.299 0.000 -0.396 -0.228
L2.e(std_sales).e(std_sales) -0.0287 0.030 -0.958 0.338 -0.088 0.030
L1.e(std_emp).e(std_emp) 0.3580 0.009 40.009 0.000 0.340 0.376
L2.e(std_emp).e(std_emp) 0.4870 0.010 50.717 0.000 0.468 0.506
================================================================================================
Ljung-Box (L1) (Q): nan, 0.15, 0.62, 6.97 Jarque-Bera (JB): nan, 10067.99, 9.30, 4015.88
Prob(Q): nan, 0.70, 0.43, 0.01 Prob(JB): nan, 0.00, 0.01, 0.00
Heteroskedasticity (H): nan, 4.25, 0.50, 0.37 Skew: nan, -0.91, 0.02, 1.12
Prob(H) (two-sided): nan, 0.00, 0.00, 0.00 Kurtosis: nan, 26.61, 3.72, 17.79
================================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/stattools.py:1431: RuntimeWarning: invalid value encountered in divide
test_statistic = numer_squared_sum / denom_squared_sum
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/stattools.py:702: RuntimeWarning: invalid value encountered in divide
acf = avf[: nlags + 1] / avf[0]
推定された因子¶
未観測因子をプロットすると役立つ場合がありますが、ここでは、次の2つの理由から、考えられるほど役立ちません。
上記の符号に関連する識別問題。
データは差分化されているため、推定された因子は元のデータではなく、差分化されたデータの変動を説明します。
これらの理由から、一致指数が作成されます(以下を参照)。
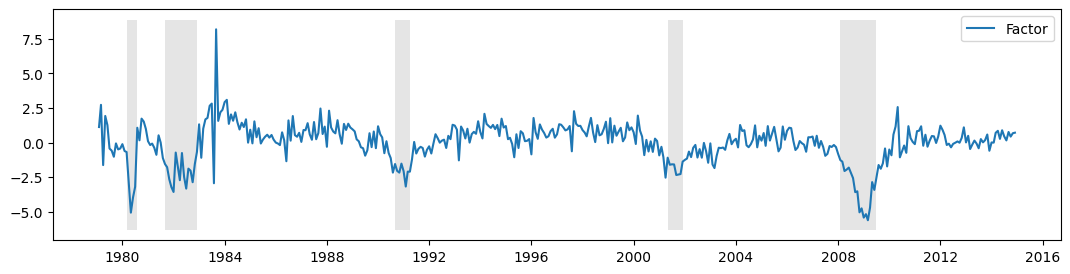
これらの留保事項を踏まえて、未観測因子は、米国の景気後退のNBER指標とともに、以下にプロットされています。この因子は、ある程度の景気循環活動を捉えることに成功しているようです。
[10]:
fig, ax = plt.subplots(figsize=(13,3))
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, res.factors.filtered[0], label='Factor')
ax.legend()
# Retrieve and also plot the NBER recession indicators
rec = DataReader('USREC', 'fred', start=start, end=end)
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);
推定後¶
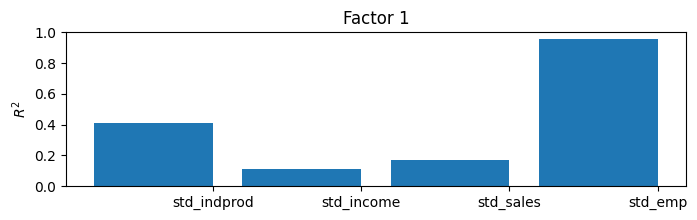
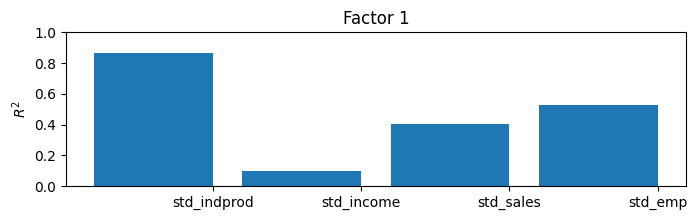
ここでは一致指数を構築することでモデルの結果を解釈できますが、推定された因子によって何が捉えられているかを理解するための有用で一般的なアプローチがあります。推定された因子を所与として、それぞれ(一度に1つずつ)を観測された各変数に回帰し、決定係数(\(R^2\) 値)を記録することにより、各因子が分散のかなりの部分を説明する変数とそうでない変数を理解することができます。
より多くの変数とより多くの因子を持つモデルでは、これは因子に解釈を与えることがあります(たとえば、ある因子は主に実変数に、別の因子は名目変数に負荷されることがあります)。
このモデルでは、内生変数が4つだけで因子が1つしかないため、\(R^2\) 値の単純な表を理解するのは簡単ですが、より大きなモデルではそうではありません。このため、棒グラフがよく使用されます。プロットから、因子が工業生産指数の変動のほとんどと、売上と雇用の変動のかなりの部分を説明していることが容易にわかりますが、所得を説明するのにはあまり役立ちません。
[11]:
res.plot_coefficients_of_determination(figsize=(8,2));
一致指数¶
上記で説明したように、このモデルの目標は、マクロ経済の現状を理解するために使用できる解釈可能な系列を作成することでした。これは、一致指数が設計された目的です。以下に構築されています。構築の説明に興味のある読者は、Kim and Nelson(1999)またはStock and Watson(1991)を参照してください。
本質的に行われていることは、(差分)因子の平均を再構築することです。これを、フィラデルフィア連邦準備銀行(FREDのUSPHCI)が公表している一致指数と比較します。
[12]:
usphci = DataReader('USPHCI', 'fred', start='1979-01-01', end='2014-12-01')['USPHCI']
usphci.plot(figsize=(13,3));
[13]:
dusphci = usphci.diff()[1:].values
def compute_coincident_index(mod, res):
# Estimate W(1)
spec = res.specification
design = mod.ssm['design']
transition = mod.ssm['transition']
ss_kalman_gain = res.filter_results.kalman_gain[:,:,-1]
k_states = ss_kalman_gain.shape[0]
W1 = np.linalg.inv(np.eye(k_states) - np.dot(
np.eye(k_states) - np.dot(ss_kalman_gain, design),
transition
)).dot(ss_kalman_gain)[0]
# Compute the factor mean vector
factor_mean = np.dot(W1, dta.loc['1972-02-01':, 'dln_indprod':'dln_emp'].mean())
# Normalize the factors
factor = res.factors.filtered[0]
factor *= np.std(usphci.diff()[1:]) / np.std(factor)
# Compute the coincident index
coincident_index = np.zeros(mod.nobs+1)
# The initial value is arbitrary; here it is set to
# facilitate comparison
coincident_index[0] = usphci.iloc[0] * factor_mean / dusphci.mean()
for t in range(0, mod.nobs):
coincident_index[t+1] = coincident_index[t] + factor[t] + factor_mean
# Attach dates
coincident_index = pd.Series(coincident_index, index=dta.index).iloc[1:]
# Normalize to use the same base year as USPHCI
coincident_index *= (usphci.loc['1992-07-01'] / coincident_index.loc['1992-07-01'])
return coincident_index
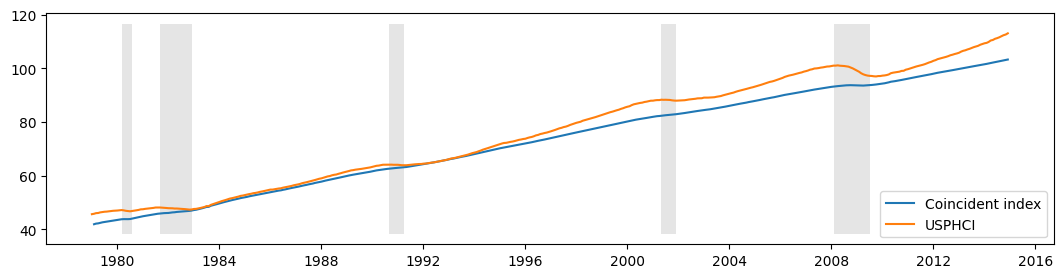
以下では、計算された一致指数を、米国の景気後退と比較一致指数USPHCIとともにプロットします。
[14]:
fig, ax = plt.subplots(figsize=(13,3))
# Compute the index
coincident_index = compute_coincident_index(mod, res)
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, coincident_index, label='Coincident index')
ax.plot(usphci.index._mpl_repr(), usphci, label='USPHCI')
ax.legend(loc='lower right')
# Retrieve and also plot the NBER recession indicators
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);
付録1:動的因子モデルの拡張¶
前の仕様は次のように記述されていたことを思い出してください。
状態空間形式で記述すると、モデルの以前の仕様は次の観測方程式を持っていました
そして遷移方程式
DynamicFactor モデルは状態空間表現の設定を処理し、DynamicFactor.update メソッドでは、適切な場所にフィッティングされたパラメータ値を入力します。
拡張された仕様は、前の例と同じですが、雇用が因子の遅延値にも依存できるようにしたい点が異なります。これにより、\(y_{\text{emp},t}\) 方程式に変更が生じます。これで、次のようになります。
ここで、対応する観測方程式は次のようになります。
\(f_{t-2}\) と \(f_{t-3}\) という2つの新しい状態変数を導入したことに注意してください。つまり、遷移方程式を更新する必要があります。
このモデルは、DynamicFactor クラスではそのまま処理できませんが、状態空間表現を適切な方法で変更するサブクラスを作成することで処理できます。
まず、factor_order = 4 に設定した場合、ほぼ目的のものが得られることに注意してください。その場合、観測方程式の最後の行は次のようになります。
そして遷移方程式の最初の行は次のようになります。
私たちが望むものと比較して、次の違いがあります。
上記の状況では、\(\lambda_{\text{emp}, j}\) は \(j > 0\) の場合ゼロに強制されますが、パラメータとして推定したいと考えています。
因子がAR(2)に従ってのみ遷移するようにしたいのですが、上記の状況ではAR(4)です。
私たちの戦略は、DynamicFactor のサブクラスを作成し、factor_order = 4 であると仮定するほとんどの作業(状態空間表現の設定など)を実行させることです。サブクラスで実際に行うことは、これら2つの問題を修正することだけです。
まず、サブクラスの完全なコードを以下に示します。以下で説明します。最初に、以下に定義されているメソッドはいずれも省略できなかったことに注意することが重要です。実際、メソッド __init__、start_params、param_names、transform_params、untransform_params、および update は、DynamicFactor クラスだけでなく、statsmodelsのすべての状態空間モデルの中核を形成します。
[15]:
from statsmodels.tsa.statespace import tools
class ExtendedDFM(sm.tsa.DynamicFactor):
def __init__(self, endog, **kwargs):
# Setup the model as if we had a factor order of 4
super(ExtendedDFM, self).__init__(
endog, k_factors=1, factor_order=4, error_order=2,
**kwargs)
# Note: `self.parameters` is an ordered dict with the
# keys corresponding to parameter types, and the values
# the number of parameters of that type.
# Add the new parameters
self.parameters['new_loadings'] = 3
# Cache a slice for the location of the 4 factor AR
# parameters (a_1, ..., a_4) in the full parameter vector
offset = (self.parameters['factor_loadings'] +
self.parameters['exog'] +
self.parameters['error_cov'])
self._params_factor_ar = np.s_[offset:offset+2]
self._params_factor_zero = np.s_[offset+2:offset+4]
@property
def start_params(self):
# Add three new loading parameters to the end of the parameter
# vector, initialized to zeros (for simplicity; they could
# be initialized any way you like)
return np.r_[super(ExtendedDFM, self).start_params, 0, 0, 0]
@property
def param_names(self):
# Add the corresponding names for the new loading parameters
# (the name can be anything you like)
return super(ExtendedDFM, self).param_names + [
'loading.L%d.f1.%s' % (i, self.endog_names[3]) for i in range(1,4)]
def transform_params(self, unconstrained):
# Perform the typical DFM transformation (w/o the new parameters)
constrained = super(ExtendedDFM, self).transform_params(
unconstrained[:-3])
# Redo the factor AR constraint, since we only want an AR(2),
# and the previous constraint was for an AR(4)
ar_params = unconstrained[self._params_factor_ar]
constrained[self._params_factor_ar] = (
tools.constrain_stationary_univariate(ar_params))
# Return all the parameters
return np.r_[constrained, unconstrained[-3:]]
def untransform_params(self, constrained):
# Perform the typical DFM untransformation (w/o the new parameters)
unconstrained = super(ExtendedDFM, self).untransform_params(
constrained[:-3])
# Redo the factor AR unconstrained, since we only want an AR(2),
# and the previous unconstrained was for an AR(4)
ar_params = constrained[self._params_factor_ar]
unconstrained[self._params_factor_ar] = (
tools.unconstrain_stationary_univariate(ar_params))
# Return all the parameters
return np.r_[unconstrained, constrained[-3:]]
def update(self, params, transformed=True, **kwargs):
# Peform the transformation, if required
if not transformed:
params = self.transform_params(params)
params[self._params_factor_zero] = 0
# Now perform the usual DFM update, but exclude our new parameters
super(ExtendedDFM, self).update(params[:-3], transformed=True, **kwargs)
# Finally, set our new parameters in the design matrix
self.ssm['design', 3, 1:4] = params[-3:]
では、私たちは一体何をしたのでしょうか?
``__init__``
ここでの重要なステップは、操作対象となる基本的な動的因子モデルを指定することでした。特に、上記で説明したように、最終的には因子のAR(2)モデルになるとしても、factor_order=4で初期化します。また、一般的なセットアップ関連のタスクもいくつか実行しました。
``start_params``
start_paramsは、オプティマイザの初期値として使用されます。3つの新しいパラメータを追加しているので、それらを渡す必要があります。これを行わない場合、オプティマイザはデフォルトの開始値を使用しますが、これは3つの要素が不足しています。
``param_names``
param_namesはさまざまな場所で使用されますが、特に結果クラスで使用されます。以下では、すべてのパラメータに関連付けられた名前がある場合にのみ可能な、完全な結果の概要を取得します。
``transform_params`` と ``untransform_params``
オプティマイザは、制約のない方法でパラメータ値を選択する可能性があります。これは通常は望ましくありません(たとえば、分散は負になることはできません)。transform_paramsは、オプティマイザで使用される制約のない値を、モデルに適した制約のある値に変換するために使用されます。分散項は通常2乗され(正になるように強制されます)、ARラグ係数は定常モデルになるように制約されることがよくあります。untransform_paramsは逆の操作に使用されます(開始パラメータは通常モデルに適した値で指定され、最適化ルーチンを開始する前にオプティマイザに適したパラメータに変換する必要があるため、重要です)。
新しいパラメータを変換または逆変換する必要はありませんが(負荷は理論的には任意の値を取ることができます)、2つの理由でこの関数を変更する必要があります
DynamicFactorクラスのバージョンは、現在よりも3つ少ないパラメータを想定しています。少なくとも、3つの新しいパラメータを処理する必要があります。DynamicFactorクラスのバージョンは、AR(4)モデルであるかのように、因子ラグ係数を定常になるように制約します。実際にはAR(2)モデルがあるので、制約をやり直す必要があります。また、ここで最後の2つの自己回帰係数をゼロに設定します。
``update``
新しいupdateメソッドを指定する必要がある最も重要な理由は、状態空間定式化に配置する必要がある3つの新しいパラメータがあるためです。特に、親のDynamicFactor.updateクラスに、3つの新しいパラメータを除くすべてのパラメータを状態空間表現に配置させ、最後の3つを手動で配置します。
[16]:
# Create the model
extended_mod = ExtendedDFM(endog)
initial_extended_res = extended_mod.fit(maxiter=1000, disp=False)
extended_res = extended_mod.fit(initial_extended_res.params, method='nm', maxiter=1000)
print(extended_res.summary(separate_params=False))
Optimization terminated successfully.
Current function value: 4.686378
Iterations: 279
Function evaluations: 479
Statespace Model Results
=================================================================================================================
Dep. Variable: ['std_indprod', 'std_income', 'std_sales', 'std_emp'] No. Observations: 431
Model: DynamicFactor(factors=1, order=4) Log Likelihood -2019.829
+ AR(2) errors AIC 4085.658
Date: Thu, 03 Oct 2024 BIC 4179.178
Time: 16:08:10 HQIC 4122.583
Sample: 02-01-1979
- 12-01-2014
Covariance Type: opg
====================================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------------------------
loading.f1.std_indprod -0.7064 0.036 -19.661 0.000 -0.777 -0.636
loading.f1.std_income -0.2505 0.039 -6.460 0.000 -0.327 -0.175
loading.f1.std_sales -0.4504 0.023 -19.252 0.000 -0.496 -0.405
loading.f1.std_emp -0.4117 0.038 -10.805 0.000 -0.486 -0.337
sigma2.std_indprod 0.2338 0.045 5.156 0.000 0.145 0.323
sigma2.std_income 0.8735 0.030 29.571 0.000 0.816 0.931
sigma2.std_sales 0.5226 0.035 15.117 0.000 0.455 0.590
sigma2.std_emp 0.2599 0.023 11.352 0.000 0.215 0.305
L1.f1.f1 0.2845 0.054 5.300 0.000 0.179 0.390
L2.f1.f1 0.3890 0.058 6.686 0.000 0.275 0.503
L3.f1.f1 0 3.92e-10 0 1.000 -7.68e-10 7.68e-10
L4.f1.f1 0 3.92e-10 0 1.000 -7.68e-10 7.68e-10
L1.e(std_indprod).e(std_indprod) -0.2225 0.119 -1.864 0.062 -0.456 0.011
L2.e(std_indprod).e(std_indprod) -0.1977 0.094 -2.098 0.036 -0.382 -0.013
L1.e(std_income).e(std_income) -0.2009 0.023 -8.915 0.000 -0.245 -0.157
L2.e(std_income).e(std_income) -0.0981 0.047 -2.099 0.036 -0.190 -0.006
L1.e(std_sales).e(std_sales) -0.4842 0.047 -10.269 0.000 -0.577 -0.392
L2.e(std_sales).e(std_sales) -0.2280 0.050 -4.543 0.000 -0.326 -0.130
L1.e(std_emp).e(std_emp) 0.2325 0.041 5.707 0.000 0.153 0.312
L2.e(std_emp).e(std_emp) 0.4893 0.049 10.044 0.000 0.394 0.585
loading.L1.f1.std_emp -0.0824 0.037 -2.257 0.024 -0.154 -0.011
loading.L2.f1.std_emp -0.0065 0.035 -0.185 0.854 -0.076 0.063
loading.L3.f1.std_emp -0.1730 0.028 -6.094 0.000 -0.229 -0.117
=====================================================================================================
Ljung-Box (L1) (Q): 0.13, 0.01, 1.06, 4.34 Jarque-Bera (JB): 272.57, 10233.58, 25.49, 3815.68
Prob(Q): 0.72, 0.92, 0.30, 0.04 Prob(JB): 0.00, 0.00, 0.00, 0.00
Heteroskedasticity (H): 0.75, 4.84, 0.44, 0.44 Skew: 0.26, -0.98, 0.26, 0.78
Prob(H) (two-sided): 0.08, 0.00, 0.00, 0.00 Kurtosis: 6.86, 26.79, 4.07, 17.49
=====================================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[2] Covariance matrix is singular or near-singular, with condition number 7.43e+17. Standard errors may be unstable.
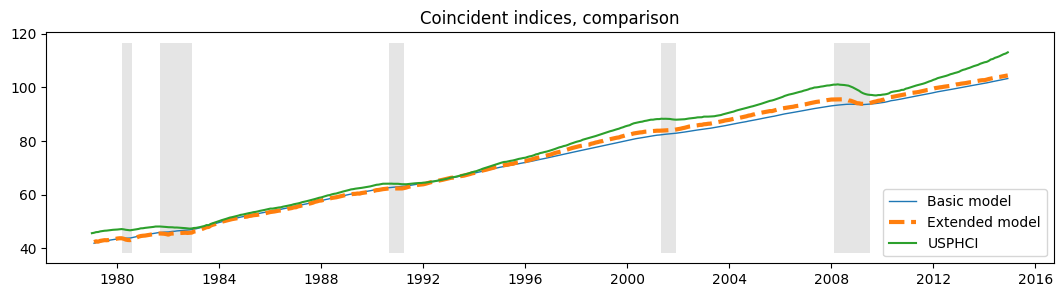
このモデルは尤度を増加させますが、追加の3つのパラメータにペナルティを課すAICおよびBICメジャーでは推奨されません。
さらに、更新された\(R^2\)チャートと新しい一致指数からわかるように、定性的な結果は変更されていません。どちらも以前の結果と実質的に同じです。
[17]:
extended_res.plot_coefficients_of_determination(figsize=(8,2));
[18]:
fig, ax = plt.subplots(figsize=(13,3))
# Compute the index
extended_coincident_index = compute_coincident_index(extended_mod, extended_res)
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, coincident_index, '-', linewidth=1, label='Basic model')
ax.plot(dates, extended_coincident_index, '--', linewidth=3, label='Extended model')
ax.plot(usphci.index._mpl_repr(), usphci, label='USPHCI')
ax.legend(loc='lower right')
ax.set(title='Coincident indices, comparison')
# Retrieve and also plot the NBER recession indicators
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);