予測、データセットの更新、そして「ニュース」¶
このノートブックでは、Statsmodelsを使用して、更新または修正されたデータセットが、サンプル外予測または欠損データのサンプル内推定に与える影響を計算する方法について説明します。「Nowcasting」文献(最後に参考文献を参照)のアプローチに従い、状態空間モデルを使用して、入ってくるデータの「ニュース」と影響を計算します。
注:このノートブックはStatsmodels v0.12以降に適用されます。さらに、sm.tsa.statespace.ExponentialSmoothing、sm.tsa.arima.ARIMA、sm.tsa.SARIMAX、sm.tsa.UnobservedComponents、sm.tsa.VARMAX、およびsm.tsa.DynamicFactorである、状態空間モデルまたは関連クラスにのみ適用されます。
[1]:
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
macrodata = sm.datasets.macrodata.load_pandas().data
macrodata.index = pd.period_range('1959Q1', '2009Q3', freq='Q')
予測演習は、多くの場合、モデル選択とパラメータ推定に使用される固定された履歴データセットから始まります。次に、適合した選択モデル(またはモデル)を使用して、サンプル外予測を作成できます。ほとんどの場合、これで話は終わりではありません。新しいデータが入ってくるにつれて、予測誤差を評価し、モデルを更新し、更新されたサンプル外予測を作成する必要がある場合があります。これは、「リアルタイム」予測演習と呼ばれることがあります(対照的に、疑似リアルタイム演習は、この手順をシミュレートするものです)。
予測誤差(MSEなど)に基づく損失関数を最小限に抑えることがすべてである場合、新しいデータが入ってきたら、更新されたデータポイントを使用して、モデル選択、パラメータ推定、およびサンプル外予測を完全にやり直すことができます。これを行うと、新しい予測は2つの理由で変化します。
新しい情報を提供する新しいデータを受け取った
予測モデルまたは推定されたパラメータが異なる
このノートブックでは、最初の効果を分離する方法に焦点を当てます。これを行う方法は、いわゆる「ナウキャスティング」文献、特にBańbura、Giannone、およびReichlin(2011)、BańburaおよびModugno(2014)、およびBańbura et al.(2014)からのものです。彼らはこの演習を「ニュース」の計算として説明しており、Statsmodelsでこの言語を使用する際に彼らに従います。
これらの方法は、複数の変数が同時に更新される可能性があり、どの更新された変数によってどの予測変更が作成されたかがすぐに明らかではないため、多変量モデルで最も役立つ場合があります。ただし、単変量モデルの予測修正について考えるのにも役立つ場合があります。したがって、最初に単純な単変量ケースから始めて、物事がどのように機能するかを説明し、その後、多変量ケースに移ります。
修正に関する注記:使用しているフレームワークは、新しく観測されたデータポイントからの予測の変更を分解するように設計されています。以前に公開されたデータポイントへの修正も考慮できますが、それらを個別に分解しません。代わりに、「修正」の全体的な効果のみを表示します。
``exog``データに関する注記:使用しているフレームワークは、モデル化された変数の新しく観測されたデータポイントからの予測の変更のみを分解します。これらはStatsmodelsでendog引数で指定される「左辺」変数です。このフレームワークは、exog引数に含まれるもののような、モデル化されていない「右辺」変数の変更を分解または考慮しません。
単純な単変量例:AR(1)¶
最初に、単純な自己回帰モデルであるAR(1)から始めます。
パラメータ \(\phi\) は系列の持続性を捉えます
このモデルを使用してインフレを予測します。
このノートブックで予測更新を簡単に説明するために、平均化されたインフレデータを使用しますが、実際には平均項でモデルを拡張するのは簡単です。
[2]:
# De-mean the inflation series
y = macrodata['infl'] - macrodata['infl'].mean()
ステップ1:利用可能なデータセットへのモデルの適合¶
ここでは、最後の5つの観測値を除くすべてのデータを使用してモデルを構築および適合させることにより、サンプル外演習をシミュレートします。これらの値をまだ観測していないと仮定し、後続のステップで分析に追加し直します。
[3]:
y_pre = y.iloc[:-5]
y_pre.plot(figsize=(15, 3), title='Inflation');
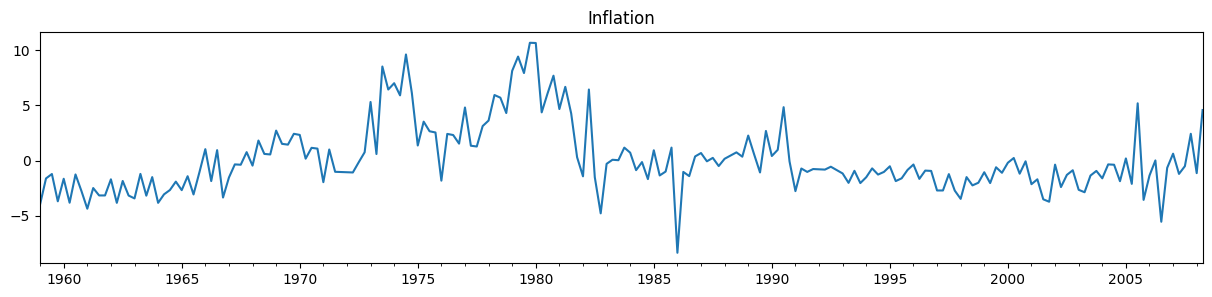
予測を構築するには、最初にモデルのパラメータを推定します。これにより、予測の生成に使用できる結果オブジェクトが返されます。
[4]:
mod_pre = sm.tsa.arima.ARIMA(y_pre, order=(1, 0, 0), trend='n')
res_pre = mod_pre.fit()
print(res_pre.summary())
SARIMAX Results
==============================================================================
Dep. Variable: infl No. Observations: 198
Model: ARIMA(1, 0, 0) Log Likelihood -446.407
Date: Thu, 03 Oct 2024 AIC 896.813
Time: 15:47:15 BIC 903.390
Sample: 03-31-1959 HQIC 899.475
- 06-30-2008
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.6751 0.043 15.858 0.000 0.592 0.759
sigma2 5.3027 0.367 14.459 0.000 4.584 6.022
===================================================================================
Ljung-Box (L1) (Q): 15.65 Jarque-Bera (JB): 43.04
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 0.85 Skew: 0.18
Prob(H) (two-sided): 0.50 Kurtosis: 5.26
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
結果オブジェクトresから予測を作成するのは簡単です。構築する予測の数を指定してforecastメソッドを呼び出すだけです。この場合、4つのサンプル外予測を構築します。
[5]:
# Compute the forecasts
forecasts_pre = res_pre.forecast(4)
# Plot the last 3 years of data and the four out-of-sample forecasts
y_pre.iloc[-12:].plot(figsize=(15, 3), label='Data', legend=True)
forecasts_pre.plot(label='Forecast', legend=True);
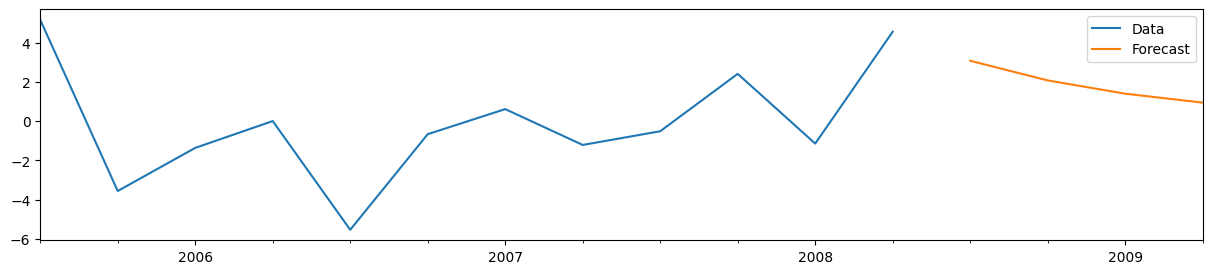
AR(1)モデルの場合、予測を手動で構築することも簡単です。最後に観測された変数を \(y_T\) とし、\(h\)ステップ先の予測を \(y_{T+h|T}\) と表記すると、次のようになります。
ここで、\(\hat \phi\) はAR(1)係数の推定値です。上記の要約出力から、これがモデルの最初のパラメータであり、結果オブジェクトのparams属性からアクセスできることがわかります。
[6]:
# Get the estimated AR(1) coefficient
phi_hat = res_pre.params[0]
# Get the last observed value of the variable
y_T = y_pre.iloc[-1]
# Directly compute the forecasts at the horizons h=1,2,3,4
manual_forecasts = pd.Series([phi_hat * y_T, phi_hat**2 * y_T,
phi_hat**3 * y_T, phi_hat**4 * y_T],
index=forecasts_pre.index)
# We'll print the two to double-check that they're the same
print(pd.concat([forecasts_pre, manual_forecasts], axis=1))
predicted_mean 0
2008Q3 3.084388 3.084388
2008Q4 2.082323 2.082323
2009Q1 1.405812 1.405812
2009Q2 0.949088 0.949088
/tmp/ipykernel_4399/554023716.py:2: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
phi_hat = res_pre.params[0]
ステップ2:新しい観測値からの「ニュース」の計算¶
時間が経過し、別の観測値を受け取ったと仮定します。データセットが大きくなり、予測誤差を評価して、後続の四半期の更新された予測を作成できます。
[7]:
# Get the next observation after the "pre" dataset
y_update = y.iloc[-5:-4]
# Print the forecast error
print('Forecast error: %.2f' % (y_update.iloc[0] - forecasts_pre.iloc[0]))
Forecast error: -10.21
更新されたデータセットに基づいて予測を計算するには、appendメソッドを使用して、前のデータセットに新しい観測値を追加することで、更新された結果オブジェクトres_postを作成します。
デフォルトでは、appendメソッドはモデルのパラメータを再推定しないことに注意してください。これはまさにここで必要なことです。新しい情報による予測への影響のみを分離したいためです。
[8]:
# Create a new results object by passing the new observations to the `append` method
res_post = res_pre.append(y_update)
# Since we now know the value for 2008Q3, we will only use `res_post` to
# produce forecasts for 2008Q4 through 2009Q2
forecasts_post = pd.concat([y_update, res_post.forecast('2009Q2')])
print(forecasts_post)
2008Q3 -7.121330
2008Q4 -4.807732
2009Q1 -3.245783
2009Q2 -2.191284
Freq: Q-DEC, dtype: float64
この場合、予測誤差は非常に大きく、インフレはAR(1)モデルの予測よりも10パーセントポイント以上低くなっています。(これは、世界的な金融危機の周辺での原油価格の大きな変動が主な原因でした)。
これをより詳細に分析するために、Statsmodelsを使用して、新しい情報の影響、つまり予測に対する「ニュース」を分離できます。これは、モデルを変更したり、パラメータを再推定したりしたくないことを意味します。代わりに、状態空間モデルの結果オブジェクトで利用可能なnewsメソッドを使用します。
Statsmodelsでニュースを計算するには、常に前の結果オブジェクトまたはデータセットと、更新された結果オブジェクトまたはデータセットが必要です。ここでは、元の結果オブジェクトres_preを前の結果として使用し、作成したばかりのres_post結果オブジェクトを更新された結果として使用します。
前と更新された結果オブジェクトまたはデータセットが得られたら、newsメソッドを呼び出すことでニュースを計算できます。ここでは、res_pre.newsを呼び出し、最初の引数は更新された結果であるres_postになります(ただし、2つの結果オブジェクトがある場合は、newsメソッドはいずれか一方で呼び出すことができます)。
最初の引数として比較オブジェクトまたはデータセットを指定することに加えて、受け入れられるさまざまな他の引数があります。最も重要なのは、考慮したい「影響期間」を指定することです。これらの「影響期間」は、対象の予測期間に対応します。つまり、これらの日付は予測修正が分解される期間を指定します。
影響期間を指定するには、start、end、およびperiodsのうち2つを渡す必要があります(Pandasのdate_rangeメソッドと同様)。時系列が関連付けられた日付または期間インデックスを持つPandasオブジェクトである場合は、以下のように、startおよびendの値として日付を渡すことができます。
[9]:
# Compute the impact of the news on the four periods that we previously
# forecasted: 2008Q3 through 2009Q2
news = res_pre.news(res_post, start='2008Q3', end='2009Q2')
# Note: one alternative way to specify these impact dates is
# `start='2008Q3', periods=4`
変数newsは、クラスNewsResultsのオブジェクトであり、res_preと比較したres_postのデータの更新、更新されたデータセットの新しい情報、および新しい情報がstartとendの間の期間の予測に与えた影響に関する詳細が含まれています。
結果を要約する簡単な方法の1つは、summary メソッドを使用することです。
[10]:
print(news.summary())
News
===============================================================================
Model: ARIMA Original sample: 1959Q1
Date: Thu, 03 Oct 2024 - 2008Q2
Time: 15:47:16 Update through: 2008Q3
# of revisions: 0
# of new datapoints: 1
Impacts for [impacted variable = infl]
=========================================================
impact date estimate (prev) impact of news estimate (new)
---------------------------------------------------------
2008Q3 3.08 -10.21 -7.12
2008Q4 2.08 -6.89 -4.81
2009Q1 1.41 -4.65 -3.25
2009Q2 0.95 -3.14 -2.19
News from updated observations:
===================================================================
update date updated variable observed forecast (prev) news
-------------------------------------------------------------------
2008Q3 infl -7.12 3.08 -10.21
===================================================================
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 -7.12
Name: observed, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 3.08
Name: forecast (prev), dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 -10.21
Name: news, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
サマリー出力: このニュース結果オブジェクトのデフォルトのサマリーは、4つのテーブルを出力します。
モデルとデータセットのサマリー
更新されたデータからのニュースの詳細
start='2008Q3'とend='2009Q2'の間の新しい情報が予測に与える影響のサマリー更新されたデータが、
start='2008Q3'とend='2009Q2'の間の予測にどのように影響を与えたかの詳細
これらについては、以下で詳しく説明します。
注意点:
この出力を制御するために、
summaryメソッドに渡すことができる引数がいくつかあります。詳細については、ドキュメント/ドックストリングを確認してください。更新と影響の詳細を示すテーブル(4)は、モデルが多変量である場合、複数の更新がある場合、または多数の影響日が選択されている場合、非常に大きくなる可能性があります。これは、デフォルトでは単変量モデルでのみ表示されます。
1番目のテーブル:モデルとデータセットのサマリー
上記の最初のテーブルには、以下が示されています。
予測が作成されたモデルのタイプ。ここでは、AR(1) は ARIMA(p,d,q) モデルの特殊なケースであるため、ARIMA モデルです。
分析が計算された日時。
元のサンプル期間。ここでは
y_preに対応します。更新されたサンプル期間の終了点。ここでは
y_postの最後の日付です。
2番目のテーブル:更新されたデータからのニュース
このテーブルは、更新されたサンプルで更新された観測値に対する以前の結果からの予測を単純に示しています。
注意点:
更新されたデータセット
y_postには、以前に観測されたデータポイントのリビジョンは含まれていませんでした。含まれていた場合、そのようなリビジョンの以前の値と更新された値を示す追加のテーブルが表示されます。
3番目のテーブル:新しい情報の影響のサマリー
列:
上記の3番目のテーブルには、以下が示されています。
各影響日の以前の予測(「推定(以前)」列)
新しい情報(「ニュース」)が各影響日の予測に与えた影響(「ニュースの影響」列)
各影響日の更新された予測(「推定(新規)」列)
注意点:
多変量モデルでは、このテーブルには、各行の関連する影響を受けた変数を記述する追加の列が含まれています。
更新されたデータセット
y_postには、以前に観測されたデータポイントのリビジョンは含まれていませんでした。含まれていた場合、このテーブルには、それらのリビジョンが影響日の予測に与える影響を示す追加の列が表示されます。推定 (新規) = 推定 (以前) + ニュースの影響であることに注意してください。このテーブルには、
summary_impactsメソッドを使用して個別にアクセスできます。
この例では:
この例では、テーブルに以前に計算した値が表示されていることに注意してください。
「推定(以前)」列は、
forecasts_pre変数に含まれる以前のモデルからの予測と同一です。「推定(新規)」列は、2008Q3 の観測値と、2008Q4〜2009Q2 の更新されたモデルからの予測を含む
forecasts_post変数と同一です。
4番目のテーブル:更新とその影響の詳細
上記の4番目のテーブルは、各新しい観測値が各影響日でどのように特定の影響に変換されたかを示しています。
列:
最初の3つの列のテーブルは、関連する更新(「更新」は新しい観測値)について説明しています。
最初の列(「更新日」)は、更新された変数の日付を示しています。
2番目の列(「予測(以前)」)は、以前の結果/データセットに基づいて、更新日に更新変数の予測値となるはずの値を示しています。
3番目の列(「観測値」)は、更新された結果/データセットにおける、その更新された変数/更新日の実際の観測値を示しています。
最後の4つの列は、特定の更新の影響(影響とは、「影響期間」内の変更された予測)について説明しています。
4番目の列(「影響日」)は、特定の更新が影響を与えた日付を示します。
5番目の列(「ニュース」)は、特定の更新に関連付けられた「ニュース」を示しています(これは特定の更新の各影響で同じですが、デフォルトではスパース化されていません)。
6番目の列(「重み」)は、与えられた更新からの「ニュース」が、影響日に影響を受けた変数に与える重みを記述しています。一般的に、重みは「更新された変数」/「更新日」/「影響を受けた変数」/「影響日」の組み合わせごとに異なります。
7番目の列(「影響」)は、特定の更新が、与えられた「影響を受けた変数」/「影響日」に与えた影響を示します。
注意点:
多変量モデルでは、このテーブルには、更新された関連変数と、各行の影響を受けた変数を示す追加の列が含まれています。ここでは、1つの変数(「infl」)のみがあるため、スペースを節約するためにこれらの列は抑制されています。
デフォルトでは、このテーブルの更新は、「更新日」、「予測(以前)」、「観測値」の同じ値をテーブルの各行に繰り返すのを避けるために、ブランクで「スパース化」されます。この動作は、
sparsify引数を使用してオーバーライドできます。影響 = ニュース * 重みであることに注意してください。このテーブルには、
summary_detailsメソッドを使用して個別にアクセスできます。
この例では:
2008Q3への更新と影響日2008Q3の場合、重みは1に等しくなります。これは、変数が1つしかないため、2008Q3のデータを取り込んだ後、この日付の「予測」について残りのあいまいさがなくなるためです。したがって、2008Q3でのこの変数に関するすべての「ニュース」は、直接「予測」に渡されます。
補遺:ニュース、重み、および影響を手動で計算する¶
単変量モデルのこの簡単な例では、上記に示されているすべての値を手動で簡単に計算できます。まず、予測の式 \(y_{T+h|T} = \phi^h y_T\) を思い出してください。また、\(y_{T+h|T+1} = \phi^h y_{T+1}\) も同様に得られることに注意してください。最後に、\(y_{T|T+1} = y_T\) であることに注意してください。これは、\(T+1\) までの観測値の値がわかっている場合、\(y_T\) の値がわかるためです。
ニュース:「ニュース」は、新しい観測値の1つに関連付けられた予測誤差にすぎません。したがって、観測値 \(T+1\) に関連付けられたニュースは
影響:ニュースの影響とは、更新された予測と以前の予測の違いであり、\(i_h \equiv y_{T+h|T+1} - y_{T+h|T}\) です。
\(h=1, \dots, 4\) に対する以前の予測は、\(\begin{pmatrix} \phi y_T & \phi^2 y_T & \phi^3 y_T & \phi^4 y_T \end{pmatrix}'\) です。
\(h=1, \dots, 4\) に対する更新された予測は、\(\begin{pmatrix} y_{T+1} & \phi y_{T+1} & \phi^2 y_{T+1} & \phi^3 y_{T+1} \end{pmatrix}'\) です。
したがって、影響は次のとおりです。
重み:重みを計算するには、予測誤差 \(n_{T+1}\) の観点から影響を書き換えることができることに注意するだけで済みます。
重みは単純に \(w = \begin{pmatrix} 1 \\ \phi \\ \phi^2 \\ \phi^3 \end{pmatrix}\) です。
これが news メソッドで計算された内容であることを確認できます。
[11]:
# Print the news, computed by the `news` method
print(news.news)
# Manually compute the news
print()
print((y_update.iloc[0] - phi_hat * y_pre.iloc[-1]).round(6))
update date updated variable
2008Q3 infl -10.205718
Name: news, dtype: float64
-10.205718
[12]:
# Print the total impacts, computed by the `news` method
# (Note: news.total_impacts = news.revision_impacts + news.update_impacts, but
# here there are no data revisions, so total and update impacts are the same)
print(news.total_impacts)
# Manually compute the impacts
print()
print(forecasts_post - forecasts_pre)
impacted variable infl
impact date
2008Q3 -10.205718
2008Q4 -6.890055
2009Q1 -4.651595
2009Q2 -3.140371
2008Q3 -10.205718
2008Q4 -6.890055
2009Q1 -4.651595
2009Q2 -3.140371
Freq: Q-DEC, dtype: float64
[13]:
# Print the weights, computed by the `news` method
print(news.weights)
# Manually compute the weights
print()
print(np.array([1, phi_hat, phi_hat**2, phi_hat**3]).round(6))
impact date 2008Q3 2008Q4 2009Q1 2009Q2
impacted variable infl infl infl infl
update date updated variable
2008Q3 infl 1.0 0.675117 0.455783 0.307707
[1. 0.675117 0.455783 0.307707]
多変量モデルの例:動的因子¶
この例では、動的因子モデルを使用して、個人消費支出(PCE)物価指数と消費者物価指数(CPI)に基づいて、毎月のコア物価インフレを予測することを検討します。これらの指標はどちらも米国経済における物価を追跡しており、同様のソースデータに基づいていますが、定義上の違いがいくつかあります。それでも、それらは比較的よく互いに追跡するため、単一の動的因子を使用してそれらを共同でモデル化することは理にかなっているようです。
この種のアプローチが役立つ理由の1つは、CPIがPCEよりも月の早い時期に発表されることです。したがって、CPIが発表されたら、その追加のデータポイントで動的因子モデルを更新し、その月のPCEリリースに対して改善された予測を取得できます。この種の分析のより複雑なバージョンは、Knotek and Zaman(2017)で入手できます。
まず、FRED からコアCPIとPCE物価指数のデータをダウンロードし、年換算の月次インフレ率に変換し、2つの外れ値を削除し、各系列を非平均化します(動的因子モデルは平均がゼロではないため)。
[14]:
import pandas_datareader as pdr
levels = pdr.get_data_fred(['PCEPILFE', 'CPILFESL'], start='1999', end='2019').to_period('M')
infl = np.log(levels).diff().iloc[1:] * 1200
infl.columns = ['PCE', 'CPI']
# Remove two outliers and de-mean the series
infl.loc['2001-09':'2001-10', 'PCE'] = np.nan
これがどのように機能するかを示すために、2017年3月のCPI発表データである2017年4月14日であると想像します。一度に複数の更新の効果を示すことができるように、1月末以降データを更新していないと仮定します。
当社の以前のデータセットは、2017年1月までのPCEとCPIのすべての値で構成されます。
当社の更新されたデータセットには、2017年2月と3月のCPI、および2017年2月のPCEデータが追加で組み込まれます。ただし、まだPCEはありません(2017年3月のPCE物価指数は2017年5月1日までリリースされませんでした)。
[15]:
# Previous dataset runs through 2017-02
y_pre = infl.loc[:'2017-01'].copy()
const_pre = np.ones(len(y_pre))
print(y_pre.tail())
PCE CPI
DATE
2016-09 1.591601 2.022262
2016-10 1.540990 1.445830
2016-11 0.533425 1.631694
2016-12 1.393060 2.109728
2017-01 3.203951 2.623570
[16]:
# For the updated dataset, we'll just add in the
# CPI value for 2017-03
y_post = infl.loc[:'2017-03'].copy()
y_post.loc['2017-03', 'PCE'] = np.nan
const_post = np.ones(len(y_post))
# Notice the missing value for PCE in 2017-03
print(y_post.tail())
PCE CPI
DATE
2016-11 0.533425 1.631694
2016-12 1.393060 2.109728
2017-01 3.203951 2.623570
2017-02 2.123190 2.541355
2017-03 NaN -0.258197
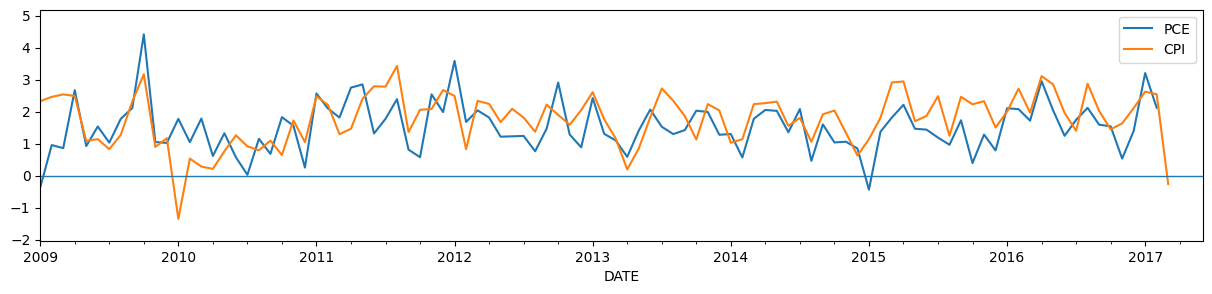
2017年3月には、コアCPI価格が2010年以来初めて下落し、この情報がその月のコアPCE価格を予測するのに役立つ可能性があるため、この特定の例を選択しました。下のグラフは、4月14日に観測されたであろうCPIとPCEの価格データを示しています\(^\dagger\)。
\(\dagger\) この記述は完全に真実ではありません。CPIとPCEの価格指数の両方が、後で一定の範囲で修正される可能性があるためです。結果として、私たちがプルしている系列は、2017年4月14日に観測されたものとまったく同じではありません。これは、FRED の代わりに ALFRED からアーカイブされたデータをプルすることで修正できますが、このチュートリアルには十分なデータです。
[17]:
# Plot the updated dataset
fig, ax = plt.subplots(figsize=(15, 3))
y_post.plot(ax=ax)
ax.hlines(0, '2009', '2017-06', linewidth=1.0)
ax.set_xlim('2009', '2017-06');
演習を実行するために、最初に DynamicFactor モデルを構築して適合させます。具体的には
単一の動的因子(
k_factors=1)を使用しています因子のダイナミクスをAR(6)モデル(
factor_order=6)でモデリングしています。作業しているインフレ系列は平均ゼロではないため、外生変数(
exog=const_pre)として1のベクトルを含めています。
[18]:
mod_pre = sm.tsa.DynamicFactor(y_pre, exog=const_pre, k_factors=1, factor_order=6)
res_pre = mod_pre.fit()
print(res_pre.summary())
This problem is unconstrained.
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 12 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 4.81947D+00 |proj g|= 3.24664D-01
At iterate 5 f= 4.62090D+00 |proj g|= 3.53739D-01
At iterate 10 f= 2.79040D+00 |proj g|= 3.87962D-01
At iterate 15 f= 2.54688D+00 |proj g|= 1.35633D-01
At iterate 20 f= 2.45463D+00 |proj g|= 1.04853D-01
At iterate 25 f= 2.42572D+00 |proj g|= 4.92521D-02
At iterate 30 f= 2.42118D+00 |proj g|= 2.82902D-02
At iterate 35 f= 2.42077D+00 |proj g|= 6.08268D-03
At iterate 40 f= 2.42076D+00 |proj g|= 1.04046D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
12 43 66 1 0 0 3.456D-05 2.421D+00
F = 2.4207581817590249
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
Statespace Model Results
=============================================================================================
Dep. Variable: ['PCE', 'CPI'] No. Observations: 216
Model: DynamicFactor(factors=1, order=6) Log Likelihood -522.884
+ 1 regressors AIC 1069.768
Date: Thu, 03 Oct 2024 BIC 1110.271
Time: 15:48:15 HQIC 1086.131
Sample: 02-28-1999
- 01-31-2017
Covariance Type: opg
===================================================================================
Ljung-Box (L1) (Q): 4.50, 0.54 Jarque-Bera (JB): 13.09, 12.63
Prob(Q): 0.03, 0.46 Prob(JB): 0.00, 0.00
Heteroskedasticity (H): 0.56, 0.44 Skew: 0.18, -0.16
Prob(H) (two-sided): 0.02, 0.00 Kurtosis: 4.15, 4.14
Results for equation PCE
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
loading.f1 0.5499 0.061 9.037 0.000 0.431 0.669
beta.const 1.7039 0.095 17.959 0.000 1.518 1.890
Results for equation CPI
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
loading.f1 0.9033 0.102 8.875 0.000 0.704 1.103
beta.const 1.9621 0.137 14.357 0.000 1.694 2.230
Results for factor equation f1
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
L1.f1 0.1246 0.069 1.805 0.071 -0.011 0.260
L2.f1 0.1823 0.072 2.548 0.011 0.042 0.323
L3.f1 0.0178 0.073 0.244 0.807 -0.125 0.160
L4.f1 -0.0700 0.078 -0.893 0.372 -0.224 0.084
L5.f1 0.1561 0.068 2.308 0.021 0.024 0.289
L6.f1 0.1376 0.075 1.842 0.066 -0.009 0.284
Error covariance matrix
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
sigma2.PCE 0.5422 0.065 8.287 0.000 0.414 0.670
sigma2.CPI 1.322e-12 0.144 9.15e-12 1.000 -0.283 0.283
==============================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
適合されたモデルを使用して、2017年3月のCPIの観測に関連するニュースと影響を構築します。更新されたデータは2017年2月と2017年3月の一部であり、3月と4月の両方への影響を調べます。
単変量の場合の例では、まず更新された結果オブジェクトを作成し、それを news メソッドに渡しました。ここでは、更新されたデータセットを直接渡すことでニュースを作成しています。
以下の点に注意してください。
y_postには、更新されたデータセット全体が含まれています(新しいデータポイントだけではありません)。また、更新された
exog配列を渡す必要もありました。この配列は、両方をカバーする必要があります。y_postに関連付けられた期間全体y_postの終了後、endで指定された最終影響日までに追加されたデータポイント
ここでは、
y_postが 2017 年 3 月に終わるため、exogは 2017 年 4 月まで延長する必要がありました。
[19]:
# Create the news results
# Note
const_post_plus1 = np.ones(len(y_post) + 1)
news = res_pre.news(y_post, exog=const_post_plus1, start='2017-03', end='2017-04')
注意:
上記の単変量の場合の例では、最初に新しい結果オブジェクトを作成し、それを
newsメソッドに渡しました。ここでも同様にできますが、追加の手順が必要です。y_postの終了を超える期間の影響を要求しているため、その期間のexog変数の追加値をnewsに渡す必要があります。res_post = res_pre.apply(y_post, exog=const_post) news = res_pre.news(res_post, exog=[1.], start='2017-03', end='2017-04')
news を計算したので、summary を表示するのが結果を確認するのに便利な方法です。
[20]:
# Show the summary of the news results
print(news.summary())
News
===============================================================================
Model: DynamicFactor Original sample: 1999-02
Date: Thu, 03 Oct 2024 - 2017-01
Time: 15:48:16 Update through: 2017-03
# of revisions: 0
# of new datapoints: 3
Impacts
===========================================================================
impact date impacted variable estimate (prev) impact of news estimate (new)
---------------------------------------------------------------------------
2017-03 CPI 2.07 -2.33 -0.26
NaT PCE 1.77 -1.42 0.35
2017-04 CPI 1.90 -0.23 1.67
NaT PCE 1.67 -0.14 1.53
News from updated observations:
===================================================================
update date updated variable observed forecast (prev) news
-------------------------------------------------------------------
2017-02 CPI 2.54 2.24 0.30
PCE 2.12 1.87 0.25
2017-03 CPI -0.26 2.07 -2.33
===================================================================
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:936: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 2.07
1 1.77
2 1.90
3 1.67
Name: estimate (prev), dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
impacts.iloc[:, 2:] = impacts.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:936: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 0.00
1 0.00
2 0.00
3 0.00
Name: impact of revisions, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
impacts.iloc[:, 2:] = impacts.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:936: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 -2.33
1 -1.42
2 -0.23
3 -0.14
Name: impact of news, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
impacts.iloc[:, 2:] = impacts.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:936: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 -2.33
1 -1.42
2 -0.23
3 -0.14
Name: total impact, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
impacts.iloc[:, 2:] = impacts.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:936: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 -0.26
1 0.35
2 1.67
3 1.53
Name: estimate (new), dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
impacts.iloc[:, 2:] = impacts.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 2.54
1 2.12
2 -0.26
Name: observed, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 2.24
1 1.87
2 2.07
Name: forecast (prev), dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/news.py:1328: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 0.30
1 0.25
2 -2.33
Name: news, dtype: object' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
data.iloc[:, 2:] = data.iloc[:, 2:].map(
複数の変数があるため、デフォルトでは、サマリーには更新されたデータからのニュースと合計インパクトのみが表示されます。
最初の表から、更新されたデータセットには 3 つの新しいデータポイントが含まれており、これらのデータからの「ニュース」のほとんどは 2017 年 3 月の非常に低い数値から来ていることがわかります。
2 番目の表は、これらの 3 つのデータポイントが 2017 年 3 月の PCE の推定値に大幅な影響を与えたことを示しています(まだ観測されていません)。この推定値は約 1.5 パーセントポイント下方修正されました。
更新されたデータは、最初のサンプル外の月である 2017 年 4 月の予測にも影響を与えました。新しいデータを組み込んだ後、その月の CPI および PCE インフレに対するモデルの予測は、それぞれ 0.29 および 0.17 パーセントポイント下方修正されました。
これらの表は「ニュース」と合計インパクトを示していますが、各インパクトが更新されたデータポイントによってどれだけ引き起こされたかは示していません。その情報を確認するには、詳細表を見る必要があります。
詳細表を確認する方法の 1 つは、include_details=True を summary メソッドに渡すことです。ただし、上記の表を繰り返さないように、summary_details メソッドを直接呼び出します。
[21]:
print(news.summary_details())
Details of news for [updated variable = CPI]
======================================================================================================
update date observed forecast (prev) impact date impacted variable news weight impact
------------------------------------------------------------------------------------------------------
2017-02 2.54 2.24 2017-04 CPI 0.30 0.18 0.06
PCE 0.30 0.11 0.03
2017-03 -0.26 2.07 2017-03 CPI -2.33 1.0 -2.33
PCE -2.33 0.61 -1.42
2017-04 CPI -2.33 0.12 -0.29
PCE -2.33 0.08 -0.18
======================================================================================================
この表は、上記の 2017 年 4 月の PCE の推定値に対する修正のほとんどが、2017 年 3 月の CPI リリースに関連するニュースから来ていることを示しています。対照的に、2 月の CPI リリースは 4 月の予測にほとんど影響を与えず、2 月の PCE リリースは本質的に影響を与えませんでした。
参考文献¶
Bańbura, Marta, Domenico Giannone, and Lucrezia Reichlin. “Nowcasting.” The Oxford Handbook of Economic Forecasting. July 8, 2011.
Bańbura, Marta, Domenico Giannone, Michele Modugno, and Lucrezia Reichlin. “Now-casting and the real-time data flow.” In Handbook of economic forecasting, vol. 2, pp. 195-237. Elsevier, 2013.
Bańbura, Marta, and Michele Modugno. “Maximum likelihood estimation of factor models on datasets with arbitrary pattern of missing data.” Journal of Applied Econometrics 29, no. 1 (2014): 133-160.
Knotek, Edward S., and Saeed Zaman. “Nowcasting US headline and core inflation.” Journal of Money, Credit and Banking 49, no. 5 (2017): 931-968.