SARIMAX:はじめに¶
このノートブックは、StataのARIMA時系列推定および推定後分析のドキュメントからの例を再現しています。
まず、4つの推定例を再現します。http://www.stata.com/manuals13/tsarima.pdf
米国卸売物価指数(WPI)データセットに対するARIMA(1,1,1)モデル。
加法季節効果を許容するために、ARIMA(1,1,1)の仕様にMA(4)項を追加した例1のバリエーション。
月次航空会社データのARIMA(2,1,0)x(1,1,0,12)モデル。この例では、乗法季節効果を許容しています。
外生変数を持つARMA(1,1)モデル。消費を自己回帰過程として記述し、マネーサプライも説明変数であると仮定しています。
次に、http://www.stata.com/manuals13/tsarimapostestimation.pdfを再現するための推定後分析機能を示します。例4のモデルを使用して、以下を示します。
1ステップ先の一時点予測
nステップ先の見本外予測
nステップ先の一時点動的予測
[1]:
%matplotlib inline
[2]:
import numpy as np
import pandas as pd
from scipy.stats import norm
import statsmodels.api as sm
import matplotlib.pyplot as plt
from datetime import datetime
import requests
from io import BytesIO
# Register converters to avoid warnings
pd.plotting.register_matplotlib_converters()
plt.rc("figure", figsize=(16,8))
plt.rc("font", size=14)
ARIMA例1:ARIMA¶
例2のグラフに見られるように、卸売物価指数(WPI)は時間とともに増加しています(つまり、定常ではありません)。したがって、ARMAモデルは適切な仕様ではありません。この最初の例では、元の時系列が次数1の積分であると仮定し、その差分が定常であると仮定し、1つの自己回帰ラグと1つの移動平均ラグ、および切片項を持つモデルを適合させます。
仮定されたデータプロセスは次のとおりです。
ここで、\(c\)はARMAモデルの切片、\(\Delta\)は1階差分演算子であり、\(\epsilon_{t} \sim N(0, \sigma^2)\)と仮定します。これは、ラグ多項式を強調するために書き直すことができます(これは以下の例2で役立ちます)。
ここで、\(L\)はラグ演算子です。
Stataの出出力と以下の出力の違いの1つは、Stataが次のモデルを推定することです。
ここで、\(\beta_0\)はプロセス\(y_t\)の平均です。このモデルはstatsmodels SARIMAXクラスで推定されたモデルと同等ですが、解釈が異なります。同等性を確認するために、次のように注意してください。
したがって、\(c = (1 - \phi_1) \beta_0\)です。
[3]:
# Dataset
wpi1 = requests.get('https://www.stata-press.com/data/r12/wpi1.dta').content
data = pd.read_stata(BytesIO(wpi1))
data.index = data.t
# Set the frequency
data.index.freq="QS-OCT"
# Fit the model
mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(1,1,1))
res = mod.fit(disp=False)
print(res.summary())
SARIMAX Results
==============================================================================
Dep. Variable: wpi No. Observations: 124
Model: SARIMAX(1, 1, 1) Log Likelihood -135.351
Date: Thu, 03 Oct 2024 AIC 278.703
Time: 16:05:55 BIC 289.951
Sample: 01-01-1960 HQIC 283.272
- 10-01-1990
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.0943 0.068 1.389 0.165 -0.039 0.227
ar.L1 0.8742 0.055 16.028 0.000 0.767 0.981
ma.L1 -0.4120 0.100 -4.119 0.000 -0.608 -0.216
sigma2 0.5257 0.053 9.849 0.000 0.421 0.630
===================================================================================
Ljung-Box (L1) (Q): 0.09 Jarque-Bera (JB): 9.78
Prob(Q): 0.77 Prob(JB): 0.01
Heteroskedasticity (H): 15.93 Skew: 0.28
Prob(H) (two-sided): 0.00 Kurtosis: 4.26
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
したがって、最尤推定値は、上記の過程について、次のことを意味します。
ここで、\(\epsilon_{t} \sim N(0, 0.5257)\)です。最後に、\(c = (1 - \phi_1) \beta_0\)であることを思い出してください。ここでは、\(c = 0.0943\)および\(\phi_1 = 0.8742\)です。Stataの出出力と比較するために、平均を計算できます。
**注記**:この値は、Stataのドキュメントの値\(\beta_0 = 0.7498\)とほぼ同じです。わずかな違いは、おそらく丸めと使用される数値最適化装置の停止基準の微妙な違いによるものです。
ARIMA例2:加法季節効果のあるARIMA¶
このモデルは、例1のモデルの拡張です。ここでは、データが次の過程に従うと仮定します。
このモデルの新しい部分は、年間の季節効果が許容されていることです(データセットが四半期ごとであるため、周期性は4であるにもかかわらず、年間です)。2番目の違いは、このモデルがレベルではなくデータの対数を使用することです。
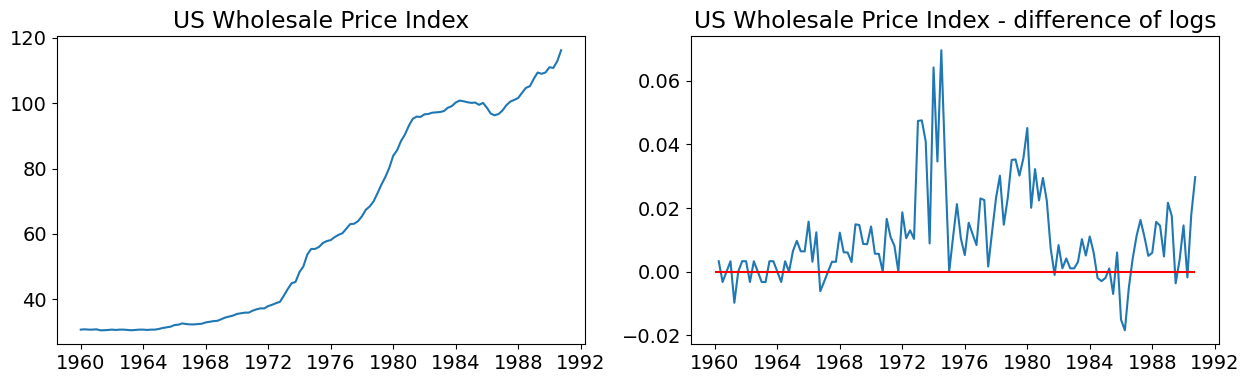
データセットを推定する前に、次のことを示すグラフを示します。
時系列(対数で)
時系列の1階差分(対数で)
自己相関関数
偏自己相関関数。
最初の2つのグラフから、元の時系列は定常ではないように見えるが、1階差分は定常に見えることに注意してください。これは、データの1階差分にARMAモデルを推定するか、積分の次数が1であるARIMAモデルを推定するかのいずれかを支持します(後者のアプローチをとっていることを思い出してください)。最後の2つのグラフは、ARMA(1,1,1)モデルの使用を支持しています。
[4]:
# Dataset
data = pd.read_stata(BytesIO(wpi1))
data.index = data.t
data.index.freq="QS-OCT"
data['ln_wpi'] = np.log(data['wpi'])
data['D.ln_wpi'] = data['ln_wpi'].diff()
[5]:
# Graph data
fig, axes = plt.subplots(1, 2, figsize=(15,4))
# Levels
axes[0].plot(data.index._mpl_repr(), data['wpi'], '-')
axes[0].set(title='US Wholesale Price Index')
# Log difference
axes[1].plot(data.index._mpl_repr(), data['D.ln_wpi'], '-')
axes[1].hlines(0, data.index[0], data.index[-1], 'r')
axes[1].set(title='US Wholesale Price Index - difference of logs');
[6]:
# Graph data
fig, axes = plt.subplots(1, 2, figsize=(15,4))
fig = sm.graphics.tsa.plot_acf(data.iloc[1:]['D.ln_wpi'], lags=40, ax=axes[0])
fig = sm.graphics.tsa.plot_pacf(data.iloc[1:]['D.ln_wpi'], lags=40, ax=axes[1])
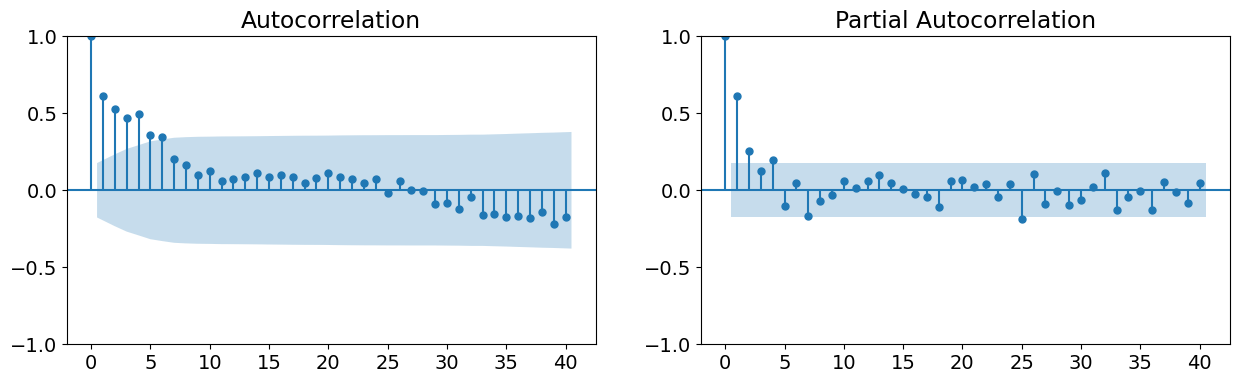
statsmodelsでこのモデルを指定する方法を理解するために、まず例1でARIMA(1,1,1)モデルを指定するために次のコードを使用したことを思い出してください。
mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(1,1,1))
order引数は、(AR 仕様、積分次数、MA 仕様)の形式のタプルです。積分次数は整数である必要があります(たとえば、ここでは1つの積分次数を仮定したので、1として指定されました。基礎となるデータがすでに定常である純粋なARMAモデルでは、0になります)。
AR仕様とMA仕様のコンポーネントには、2つの可能性があります。1つは、対応するラグ多項式の**最大次数**を指定することであり、その場合、コンポーネントは整数になります。たとえば、ARIMA(1,1,4)過程を指定する場合は、
mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(1,1,4))
を使用し、対応するデータプロセスは次のようになります。
または
仕様パラメータがラグ多項式の最大次数として指定されている場合、その次数までのすべての多項式項が含まれることを意味します。\(\epsilon_{t-2}\)と\(\epsilon_{t-3}\)の項が含まれ、ここでは不要であるため、これは使用したいモデルではありません。
必要なのは、1次と4次の項を持つ多項式であり、2次と3次の項は除外されます。そのためには、仕様パラメータにタプルを提供する必要があります。タプルは**ラグ多項式自体**を記述します。特に、ここでは次のを使用する必要があります。
ar = 1 # this is the maximum degree specification
ma = (1,0,0,1) # this is the lag polynomial specification
mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(ar,1,ma)))
これは、データのプロセスに次の形式を与えます。
これは必要なものです。
[7]:
# Fit the model
mod = sm.tsa.statespace.SARIMAX(data['ln_wpi'], trend='c', order=(1,1,(1,0,0,1)))
res = mod.fit(disp=False)
print(res.summary())
SARIMAX Results
=================================================================================
Dep. Variable: ln_wpi No. Observations: 124
Model: SARIMAX(1, 1, [1, 4]) Log Likelihood 386.034
Date: Thu, 03 Oct 2024 AIC -762.067
Time: 16:06:14 BIC -748.006
Sample: 01-01-1960 HQIC -756.355
- 10-01-1990
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.0024 0.002 1.485 0.138 -0.001 0.006
ar.L1 0.7808 0.094 8.269 0.000 0.596 0.966
ma.L1 -0.3993 0.126 -3.174 0.002 -0.646 -0.153
ma.L4 0.3087 0.120 2.572 0.010 0.073 0.544
sigma2 0.0001 9.8e-06 11.114 0.000 8.97e-05 0.000
===================================================================================
Ljung-Box (L1) (Q): 0.02 Jarque-Bera (JB): 45.15
Prob(Q): 0.90 Prob(JB): 0.00
Heteroskedasticity (H): 2.58 Skew: 0.29
Prob(H) (two-sided): 0.00 Kurtosis: 5.91
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
ARIMA例3:航空会社モデル¶
前の例では、季節効果を加法性の方法で含めました。これは、過程が4次のMAラグに依存することを許容する項を加えたことを意味します。代わりに、乗法的な方法で季節効果をモデル化したい場合があります。その場合、モデルはしばしばARIMA \((p,d,q) \times (P,D,Q)_s\)と記述されます。ここで、小文字は非季節成分の仕様を示し、大文字は季節成分の仕様を示します。\(s\)は季節の周期性です(例:四半期データの場合は4、月次データの場合は12が多い)。データ過程は一般的に次のように記述できます。
ここで
\(\phi_p (L)\)は非季節自己回帰ラグ多項式
\(\tilde \phi_P (L^s)\)は季節自己回帰ラグ多項式
\(\Delta^d \Delta_s^D y_t\)は、\(d\)回差分され、\(D\)回季節差分された時系列データです。
\(A(t)\)はトレンド多項式(切片を含む)
\(\theta_q (L)\)は非季節移動平均ラグ多項式
\(\tilde \theta_Q (L^s)\)は季節移動平均ラグ多項式
これを次のように書き直すこともあります。
ここで \(y_t^* = \Delta^d \Delta_s^D y_t\)です。これは、単純な場合と同様に、データの定常性を得るために差分(ここでは非季節と季節の両方)を取った後、結果として得られるモデルは単なるARMAモデルであることを強調しています。
例として、切片を持つ航空会社モデルARIMA \((2,1,0) \times (1,1,0)_{12}\)を考えます。データ過程は上記のように次のように記述できます。
ここでは、
\(\phi_p (L) = (1 - \phi_1 L - \phi_2 L^2)\)
\(\tilde \phi_P (L^s) = (1 - \phi_1 L^{12})\)
\(d = 1, D = 1, s=12\)は、\(y_t^*\)が\(y_t\)からまず1階差分を取り、次に12階差分を取ることで導出されることを示しています。
\(A(t) = c\)は定数トレンド多項式です(つまり、単なる切片です)
\(\theta_q (L) = \tilde \theta_Q (L^s) = 1\)(つまり、移動平均効果はありません)
時系列変数の前に2つのラグ多項式があるのを見るのはまだ分かりにくいかもしれませんが、これらのラグ多項式を掛け合わせると、次のモデルが得られることに注意してください。
これは次のように書き直すことができます。
これは例2の加法的な季節モデルに似ていますが、自己回帰ラグの前にある係数は、実際には基礎となる季節的パラメータと非季節的パラメータの組み合わせです。
statsmodelsでモデルを指定するには、seasonal_order引数を追加するだけで済みます。これは(季節AR仕様、季節積分次数、季節MA、季節周期性)の形式のタプルを受け入れます。前述のように、季節ARとMAの仕様は、最大多項式の次数、またはラグ多項式自体として表現できます。季節周期性は整数です。
切片付きの航空会社モデルARIMA \((2,1,0) \times (1,1,0)_{12}\) のコマンドは次のとおりです。
mod = sm.tsa.statespace.SARIMAX(data['lnair'], order=(2,1,0), seasonal_order=(1,1,0,12))
[8]:
# Dataset
air2 = requests.get('https://www.stata-press.com/data/r12/air2.dta').content
data = pd.read_stata(BytesIO(air2))
data.index = pd.date_range(start=datetime(int(data.time[0]), 1, 1), periods=len(data), freq='MS')
data['lnair'] = np.log(data['air'])
# Fit the model
mod = sm.tsa.statespace.SARIMAX(data['lnair'], order=(2,1,0), seasonal_order=(1,1,0,12), simple_differencing=True)
res = mod.fit(disp=False)
print(res.summary())
SARIMAX Results
==========================================================================================
Dep. Variable: D.DS12.lnair No. Observations: 131
Model: SARIMAX(2, 0, 0)x(1, 0, 0, 12) Log Likelihood 240.821
Date: Thu, 03 Oct 2024 AIC -473.643
Time: 16:06:19 BIC -462.142
Sample: 02-01-1950 HQIC -468.970
- 12-01-1960
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.4057 0.080 -5.045 0.000 -0.563 -0.248
ar.L2 -0.0799 0.099 -0.809 0.419 -0.274 0.114
ar.S.L12 -0.4723 0.072 -6.592 0.000 -0.613 -0.332
sigma2 0.0014 0.000 8.403 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.01 Jarque-Bera (JB): 0.72
Prob(Q): 0.91 Prob(JB): 0.70
Heteroskedasticity (H): 0.54 Skew: 0.14
Prob(H) (two-sided): 0.04 Kurtosis: 3.23
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
ここでは、追加の引数simple_differencing=Trueを使用しました。これは、ARIMAモデルにおける積分次数がどのように処理されるかを制御します。simple_differencing=Trueの場合、endogとして提供された時系列は文字通り差分され、ARMAモデルは結果として得られる新しい時系列に適合します。これは、差分処理によって初期の期間が失われることを意味しますが、他のパッケージ(例:Stataのarimaは常に単純な差分を使用します)の結果と比較する場合、または季節周期性が大きい場合は必要になる可能性があります。
デフォルトはsimple_differencing=Falseで、この場合、積分成分は状態空間定式化の一部として実装され、元のデータ全体を推定に使用できます。
ARIMA例4:ARMAX(Friedman)¶
このモデルは、説明変数(ARMAXのX部分)の使用を示しています。外生回帰変数が含まれている場合、SARIMAXモジュールは「SARIMA誤差を持つ回帰」の概念を使用します(ARIMA誤差を持つ回帰と代替仕様の詳細については、http://robjhyndman.com/hyndsight/arimax/を参照してください)。そのため、モデルは次のように指定されます。
最初の式は単なる線形回帰であり、2番目の式は誤差成分がSARIMAに従う過程を記述していることに注意してください(例3で説明したとおりです)。この仕様の1つの理由は、推定されたパラメータが自然な解釈を持つことです。
この仕様は、多くの単純な仕様を包含します。例えば、AR(2)誤差を持つ回帰は次のようになります。
この例で考慮されるモデルは、ARMA(1,1)誤差を持つ回帰です。この過程は次のように記述されます。
\(\beta_0\)は、上記の例1で説明したように、trend='c'で指定された切片とは異なることに注意してください。上記の例では、トレンド多項式を使用してモデルの切片を推定しましたが、ここでは、外生データセットに定数を追加することで\(\beta_0\)自体を推定する方法を示します。出力では、\(\beta_0\)はconstと呼ばれ、上記では切片\(c\)は出力でinterceptと呼ばれていました。
[9]:
# Dataset
friedman2 = requests.get('https://www.stata-press.com/data/r12/friedman2.dta').content
data = pd.read_stata(BytesIO(friedman2))
data.index = data.time
data.index.freq = "QS-OCT"
# Variables
endog = data.loc['1959':'1981', 'consump']
exog = sm.add_constant(data.loc['1959':'1981', 'm2'])
# Fit the model
mod = sm.tsa.statespace.SARIMAX(endog, exog, order=(1,0,1))
res = mod.fit(disp=False)
print(res.summary())
SARIMAX Results
==============================================================================
Dep. Variable: consump No. Observations: 92
Model: SARIMAX(1, 0, 1) Log Likelihood -340.508
Date: Thu, 03 Oct 2024 AIC 691.015
Time: 16:06:21 BIC 703.624
Sample: 01-01-1959 HQIC 696.105
- 10-01-1981
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -36.0606 56.643 -0.637 0.524 -147.078 74.957
m2 1.1220 0.036 30.824 0.000 1.051 1.193
ar.L1 0.9348 0.041 22.717 0.000 0.854 1.015
ma.L1 0.3091 0.089 3.488 0.000 0.135 0.483
sigma2 93.2556 10.889 8.565 0.000 71.914 114.597
===================================================================================
Ljung-Box (L1) (Q): 0.04 Jarque-Bera (JB): 23.49
Prob(Q): 0.84 Prob(JB): 0.00
Heteroskedasticity (H): 22.51 Skew: 0.17
Prob(H) (two-sided): 0.00 Kurtosis: 5.45
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
ARIMA推定後:例1 - 動的予測¶
ここでは、statsmodelsのSARIMAXの推定後の機能の一部について説明します。
まず、例のモデルを使用して、最後のいくつかの観測値を除外したデータを使用してパラメータを推定します(これは例としては少し人工的ですが、サンプル外予測のパフォーマンスを考慮し、Stataのドキュメントとの比較を容易にします)。
[10]:
# Dataset
raw = pd.read_stata(BytesIO(friedman2))
raw.index = raw.time
raw.index.freq = "QS-OCT"
data = raw.loc[:'1981']
# Variables
endog = data.loc['1959':, 'consump']
exog = sm.add_constant(data.loc['1959':, 'm2'])
nobs = endog.shape[0]
# Fit the model
mod = sm.tsa.statespace.SARIMAX(endog.loc[:'1978-01-01'], exog=exog.loc[:'1978-01-01'], order=(1,0,1))
fit_res = mod.fit(disp=False, maxiter=250)
print(fit_res.summary())
SARIMAX Results
==============================================================================
Dep. Variable: consump No. Observations: 77
Model: SARIMAX(1, 0, 1) Log Likelihood -243.316
Date: Thu, 03 Oct 2024 AIC 496.633
Time: 16:06:22 BIC 508.352
Sample: 01-01-1959 HQIC 501.320
- 01-01-1978
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.6782 18.492 0.037 0.971 -35.565 36.922
m2 1.0379 0.021 50.329 0.000 0.997 1.078
ar.L1 0.8775 0.059 14.859 0.000 0.762 0.993
ma.L1 0.2771 0.108 2.572 0.010 0.066 0.488
sigma2 31.6979 4.683 6.769 0.000 22.520 40.876
===================================================================================
Ljung-Box (L1) (Q): 0.32 Jarque-Bera (JB): 6.05
Prob(Q): 0.57 Prob(JB): 0.05
Heteroskedasticity (H): 6.09 Skew: 0.57
Prob(H) (two-sided): 0.00 Kurtosis: 3.76
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
次に、データセット全体の結果を取得しますが、(データのサブセットで)推定されたパラメータを使用します。
[11]:
mod = sm.tsa.statespace.SARIMAX(endog, exog=exog, order=(1,0,1))
res = mod.filter(fit_res.params)
predictコマンドは、最初にサンプル内予測を取得するためにここで適用されます。full_results=True引数を使用して、信頼区間を計算できます(predictのデフォルト出力は予測値のみです)。
他の引数がない場合、predictは、サンプル全体の1ステップ先サンプル内予測を返します。
[12]:
# In-sample one-step-ahead predictions
predict = res.get_prediction()
predict_ci = predict.conf_int()
動的予測も取得できます。1ステップ先予測は、各ステップで内生変数の真の値を使用して、次のサンプル内値を予測します。動的予測は、データセットのある時点まで(dynamic引数で指定)1ステップ先予測を使用します。その後、新しい予測要素ごとに、前の予測された内生変数の値が真の内生変数の値の代わりに使用されます。
dynamic引数は、start引数に対するオフセットとして指定されます。startが指定されていない場合、0とみなされます。
ここでは、1978年第1四半期から始まる動的予測を実行します。
[13]:
# Dynamic predictions
predict_dy = res.get_prediction(dynamic='1978-01-01')
predict_dy_ci = predict_dy.conf_int()
1ステップ先予測と動的予測(および対応する信頼区間)をグラフ化して、それらの相対的なパフォーマンスを確認できます。動的予測が始まる時点(1978年第1四半期)までは、両方が同じであることに注意してください。
[14]:
# Graph
fig, ax = plt.subplots(figsize=(9,4))
npre = 4
ax.set(title='Personal consumption', xlabel='Date', ylabel='Billions of dollars')
# Plot data points
data.loc['1977-07-01':, 'consump'].plot(ax=ax, style='o', label='Observed')
# Plot predictions
predict.predicted_mean.loc['1977-07-01':].plot(ax=ax, style='r--', label='One-step-ahead forecast')
ci = predict_ci.loc['1977-07-01':]
ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], color='r', alpha=0.1)
predict_dy.predicted_mean.loc['1977-07-01':].plot(ax=ax, style='g', label='Dynamic forecast (1978)')
ci = predict_dy_ci.loc['1977-07-01':]
ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], color='g', alpha=0.1)
legend = ax.legend(loc='lower right')
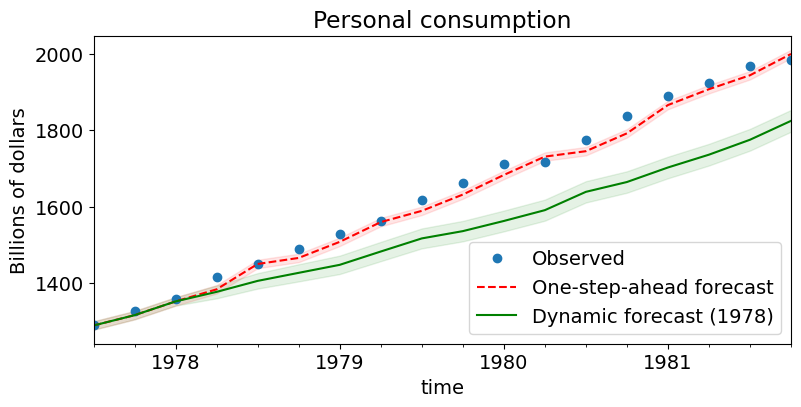
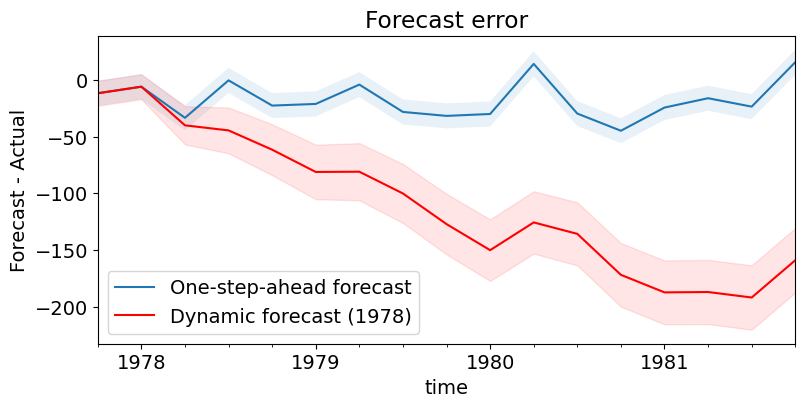
最後に、予測誤差をグラフ化します。予想どおり、1ステップ先予測の方がかなり優れていることは明らかです。
[15]:
# Prediction error
# Graph
fig, ax = plt.subplots(figsize=(9,4))
npre = 4
ax.set(title='Forecast error', xlabel='Date', ylabel='Forecast - Actual')
# In-sample one-step-ahead predictions and 95% confidence intervals
predict_error = predict.predicted_mean - endog
predict_error.loc['1977-10-01':].plot(ax=ax, label='One-step-ahead forecast')
ci = predict_ci.loc['1977-10-01':].copy()
ci.iloc[:,0] -= endog.loc['1977-10-01':]
ci.iloc[:,1] -= endog.loc['1977-10-01':]
ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], alpha=0.1)
# Dynamic predictions and 95% confidence intervals
predict_dy_error = predict_dy.predicted_mean - endog
predict_dy_error.loc['1977-10-01':].plot(ax=ax, style='r', label='Dynamic forecast (1978)')
ci = predict_dy_ci.loc['1977-10-01':].copy()
ci.iloc[:,0] -= endog.loc['1977-10-01':]
ci.iloc[:,1] -= endog.loc['1977-10-01':]
ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], color='r', alpha=0.1)
legend = ax.legend(loc='lower left');
legend.get_frame().set_facecolor('w')