TVP-VAR、MCMC、およびスパース シミュレーション スムージング¶
[1]:
%matplotlib inline
from importlib import reload
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
from scipy.stats import invwishart, invgamma
# Get the macro dataset
dta = sm.datasets.macrodata.load_pandas().data
dta.index = pd.date_range('1959Q1', '2009Q3', freq='QS')
背景¶
マルコフ連鎖モンテカルロ(MCMC)法による線形ガウス状態空間モデルのベイズ分析は、特にデータとモデルパラメータを条件とした観測されていない状態ベクトルの結合事後分布からのサンプリングの進歩により、近年では一般的かつ比較的簡単になってきました(特に Carter and Kohn(1994)、de Jong and Shephard(1995)、および Durbin and Koopman(2002)を参照)。これは、ギブスサンプリングMCMCアプローチに特に役立ちます。
これらの手順では、再帰的なカルマンフィルターとスムーザーの順方向/逆方向の適用を利用しますが、最近の研究では別のアプローチを採用し、状態のベクトル全体の事後結合分布を一度に構築します。特に、計量経済学的な時系列の扱いについては Chan and Jeliazkov(2009)を、より一般的な調査については McCausland et al.(2011)を参照してください。特に、事後平均と精度行列は明示的に構築され、後者はスパースバンド行列です。次に、スパースバンド行列のコレスキー分解のための効率的なアルゴリズムが利用されます。これにより、メモリコストが削減され、パフォーマンスが向上します。McCausland et al.(2011)に従って、この方法を「コレスキー因子アルゴリズム」(CFA)アプローチと呼びます。
CFAベースのシミュレーションスムーザーには、より一般的なカルマンフィルターとスムーザー(KFS)に基づくものと比較して、いくつかの利点と欠点があります。
CFAの利点:
結合事後分布の導出は比較的簡単で理解しやすい。
場合によっては、KFSアプローチよりも高速でメモリ消費量が少ない可能性があります
このノートブックの最後にある付録では、TVP-VARモデルの2つのシミュレーションスムーザーのパフォーマンスについて簡単に説明します。要約すると、1台のマシンでの簡単なテストでは、TVP-VARモデルの場合、StatsmodelsのCFAおよびKFS実装の実行時間はほぼ同じであり、両方の実装は、Chan and Jeliazkov(2009)が提供するMatlabで記述された複製コードよりも約2倍高速であることが示唆されています。
CFAの欠点:
主な欠点は、この方法が(少なくともこれまでのところ)KFSアプローチの汎用性に達していないことです。例えば
観測または状態方程式にランクが縮小された誤差項があるモデルでは使用できません。
このことの一つの意味は、自己回帰モデルの高次ラグに対応するために状態方程式に恒等式を含めるという一般的な状態空間モデルのトリックが適用できないことです。これらのモデルはCFAアプローチでも処理できますが、含まれるラグごとにわずかに異なる実装が必要になるという犠牲を伴います。
例として、状態空間形式でARMAおよびVARMAプロセスを表す標準的な方法には、観測および/または状態方程式に恒等式が含まれているため、Chan and Jeliazkov(2009)に示されている基本的な式はこれらのモデルにはすぐには適用できません。
状態初期化/事前分布で使用できる柔軟性が低くなります。
Statsmodels における実装¶
Chan and Jeliazkov(2009)に示されている基本的な式に沿ったCFAシミュレーションスムーザーがStatsmodelsに実装されました。
注記:
したがって、StatsmodelsのCFAシミュレーションスムーザーは、状態遷移が真に一次マルコフ過程である場合のみをサポートします(つまり、恒等式を使用して一次過程にスタックされたp次マルコフ過程をサポートしません)。
対照的に、StatsmodelsのKFSスムーザーは完全に一般的であり、スタックされたp次マルコフ過程や観測および状態方程式の他の恒等式を含む、任意の状態空間モデルに使用できます。
KFSまたはCFAシミュレーションスムーザーのいずれかは、simulation_smootherメソッドを使用して状態空間モデルから構築できます。基本的な考え方を示すために、まず簡単な例を検討します。
ローカルレベルモデル¶
ローカルレベルモデルは、観測された系列\(y_t\)を、永続的なトレンド\(\mu_t\)と一時的な誤差成分に分解します
このモデルは、観測誤差項\(\varepsilon_t\)と状態イノベーション項\(\eta_t\)の両方が非縮退であるため、つまり、それらの共分散行列がフルランクであるため、CFAシミュレーションスムーザーの要件を満たしています。
このモデルをインフレーションに適用し、結合状態ベクトルの事後分布からドローをシミュレートすることを検討します。つまり、サンプリングに関心があるのは、
ここで、\(\mu^t \equiv (\mu_1, \dots, \mu_T)'\)および\(y^t \equiv (y_1, \dots, y_T)'\)と定義します。
Statsmodelsでは、ローカルレベルモデルはより一般的な「観測されない成分」モデルのクラスに分類され、次のように構築できます。
[2]:
# Construct a local level model for inflation
mod = sm.tsa.UnobservedComponents(dta.infl, 'llevel')
# Fit the model's parameters (sigma2_varepsilon and sigma2_eta)
# via maximum likelihood
res = mod.fit()
print(res.params)
# Create simulation smoother objects
sim_kfs = mod.simulation_smoother() # default method is KFS
sim_cfa = mod.simulation_smoother(method='cfa') # can specify CFA method
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 2 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 2.40814D+00 |proj g|= 1.27979D-01
At iterate 5 f= 2.24982D+00 |proj g|= 9.50561D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
2 7 9 1 0 0 2.953D-07 2.250D+00
F = 2.2498167187365663
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
sigma2.irregular 3.373368
sigma2.level 0.744712
dtype: float64
This problem is unconstrained.
シミュレーションスムーザーオブジェクトsim_kfsとsim_cfaには、シミュレーションスムージングを実行するsimulateメソッドがあります。simulateが呼び出されるたびに、simulated_state属性は事後分布からの新しいシミュレーションドローで再設定されます。
以下では、最尤パラメータ推定値でのシミュレーションで、KFSとCFAのアプローチを使用して、トレンドの20個のシミュレーションパスを構築します。
[3]:
nsimulations = 20
simulated_state_kfs = pd.DataFrame(
np.zeros((mod.nobs, nsimulations)), index=dta.index)
simulated_state_cfa = pd.DataFrame(
np.zeros((mod.nobs, nsimulations)), index=dta.index)
for i in range(nsimulations):
# Apply KFS simulation smoothing
sim_kfs.simulate()
# Save the KFS simulated state
simulated_state_kfs.iloc[:, i] = sim_kfs.simulated_state[0]
# Apply CFA simulation smoothing
sim_cfa.simulate()
# Save the CFA simulated state
simulated_state_cfa.iloc[:, i] = sim_cfa.simulated_state[0]
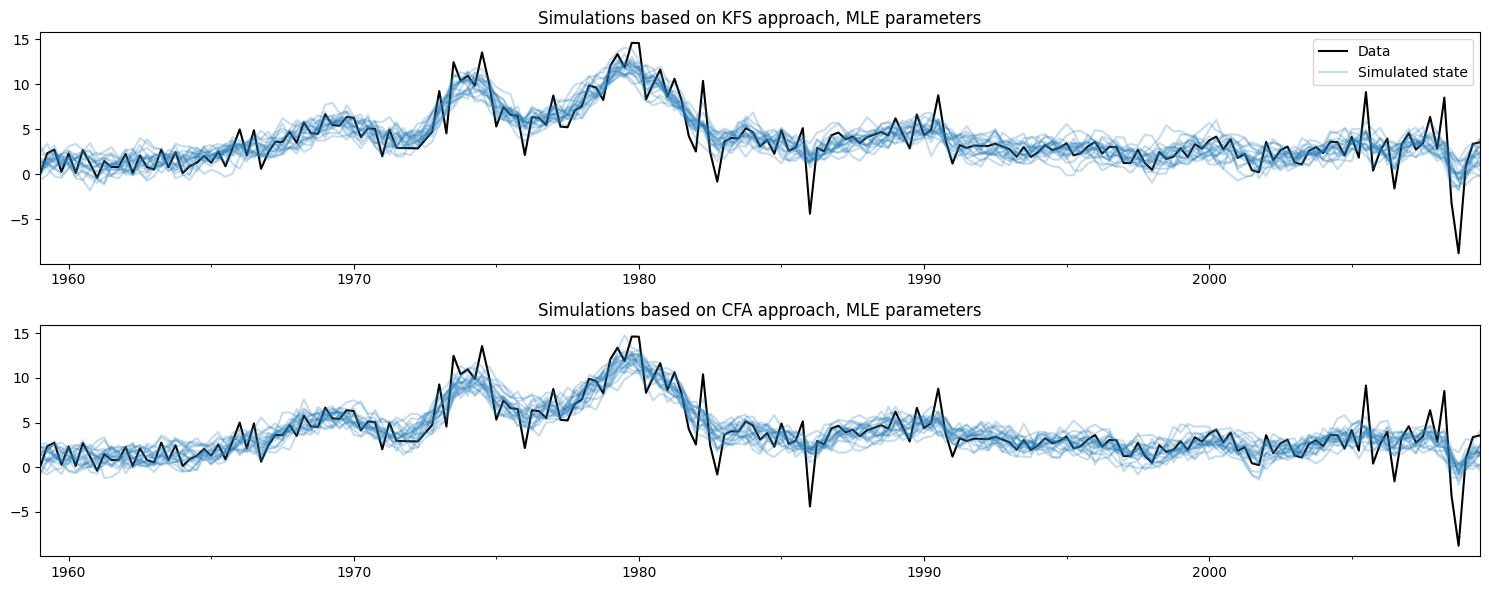
観測されたデータと、以下の各方法を使用して作成されたシミュレーションをプロットすると、これら2つの方法が同じことを行っていることが容易にわかります。
[4]:
# Plot the inflation data along with simulated trends
fig, axes = plt.subplots(2, figsize=(15, 6))
# Plot data and KFS simulations
dta.infl.plot(ax=axes[0], color='k')
axes[0].set_title('Simulations based on KFS approach, MLE parameters')
simulated_state_kfs.plot(ax=axes[0], color='C0', alpha=0.25, legend=False)
# Plot data and CFA simulations
dta.infl.plot(ax=axes[1], color='k')
axes[1].set_title('Simulations based on CFA approach, MLE parameters')
simulated_state_cfa.plot(ax=axes[1], color='C0', alpha=0.25, legend=False)
# Add a legend, clean up layout
handles, labels = axes[0].get_legend_handles_labels()
axes[0].legend(handles[:2], ['Data', 'Simulated state'])
fig.tight_layout();
モデルのパラメータの更新¶
シミュレーションスムーザーは、モデルインスタンス(ここでは変数mod)に紐付けられています。モデルインスタンスが新しいパラメータで更新されるたびに、シミュレーションスムーザーは、今後のsimulateメソッドの呼び出しで、それらの新しいパラメータを考慮に入れます。
これは、MCMCアルゴリズムに便利です。MCMCアルゴリズムは、(a)モデルのパラメータを更新し、(b)状態ベクトルのサンプルを抽出し、(c)モデルのパラメータの新しい値を抽出することを繰り返します。
ここでは、モデルをより滑らかなトレンドを生成する別のパラメータ化に変更し、シミュレーションされた値がどのように変化するかを示します(簡潔にするために、KFSアプローチからのシミュレーションのみを示しますが、CFAアプローチからのシミュレーションも同じになります)。
[5]:
fig, ax = plt.subplots(figsize=(15, 3))
# Update the model's parameterization to one that attributes more
# variation in inflation to the observation error and so has less
# variation in the trend component
mod.update([4, 0.05])
# Plot simulations
for i in range(nsimulations):
sim_kfs.simulate()
ax.plot(dta.index, sim_kfs.simulated_state[0],
color='C0', alpha=0.25, label='Simulated state')
# Plot data
dta.infl.plot(ax=ax, color='k', label='Data', zorder=-1)
# Add title, legend, clean up layout
ax.set_title('Simulations with alternative parameterization yielding a smoother trend')
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles[-2:], labels[-2:])
fig.tight_layout();

応用:MCMCによるTVP-VARモデルのベイズ分析¶
Chan and Jeliazkov(2009)が検討しているアプリケーションの1つは、ベイズギブサンプリング(MCMC)法で推定された時間変動パラメータベクトル自己回帰(TVP-VAR)モデルです。彼らはこれを、4つのマクロ経済時系列の共同運動をモデル化するために適用します
実質GDP成長率
インフレーション
失業率
短期金利
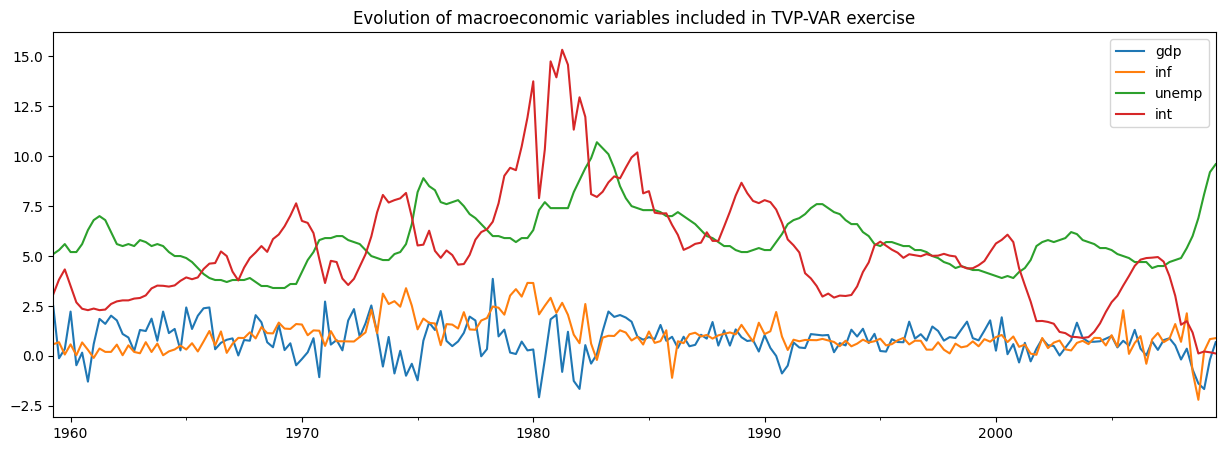
Statsmodelsに含まれている非常に類似したデータセットを使用して、彼らの例を再現します。
[6]:
# Subset to the four variables of interest
y = dta[['realgdp', 'cpi', 'unemp', 'tbilrate']].copy()
y.columns = ['gdp', 'inf', 'unemp', 'int']
# Convert to real GDP growth and CPI inflation rates
y[['gdp', 'inf']] = np.log(y[['gdp', 'inf']]).diff() * 100
y = y.iloc[1:]
fig, ax = plt.subplots(figsize=(15, 5))
y.plot(ax=ax)
ax.set_title('Evolution of macroeconomic variables included in TVP-VAR exercise');
TVP-VARモデル¶
注:このセクションはChan and Jeliazkov(2009)のセクション3.1に基づいており、詳細については参照できます。
通常の(時間不変)VAR(1)モデルは、通常次のように記述されます
ここで、\(y_t\)は時間\(t\)で観測された変数の\(p \times 1\)ベクトルであり、\(H\)は共分散行列です。
TVP-VAR(1)モデルはこれを一般化して、係数が時間とともに変化できるようにします。\(\alpha_t = \text{vec}([\mu_t : \Phi_t])\)に従ってすべてのパラメータをベクトルにスタックします。ここで、\(\text{vec}\)は行列の列をベクトルにスタックする操作を示します。時間とともに進化する様子を次のようにモデル化します。
言い換えれば、各パラメータはランダムウォークに従って独立して進化します。
\(\mu_t\)には\(p\)個の係数があり、\(\Phi_t\)には\(p^2\)個の係数があるため、完全な状態ベクトル\(\alpha\)の形状は\(p * (p + 1) \times 1\)です。
TVP-VAR(1)モデルを状態空間形式にするのは比較的簡単であり、実際には観測方程式をSUR形式に書き換えるだけで済みます
ここで
\(H\) がフルランクであり、各分散 \(\sigma_i^2\) がゼロでない限り、このモデルはCFAシミュレーション・スムーザーの要件を満たします。
初期状態 \(\alpha_1\) の初期化/事前分布も指定する必要があります。ここでは、Chan and Jeliazkov (2009) に従い、\(\alpha_1 \sim N(0, 5 I)\) を使用しますが、拡散型としてモデル化することもできます。
時間変動係数 \(\alpha_t\) に加えて、推定する必要がある他のパラメータは、共分散行列 \(H\) の要素と、ランダムウォーク分散 \(\sigma_i^2\) です。
StatsmodelsにおけるTVP-VARモデル¶
Statsmodelsでこのモデルをプログラム的に構築することも比較的簡単です。基本的には4つのステップがあります。
sm.tsa.statespace.MLEModelのサブクラスとして新しいTVPVARクラスを作成します。状態空間システムの行列の固定値を埋めます。
\(\alpha_1\) の初期化を指定します。
共分散行列 \(H\) およびランダムウォーク分散 \(\sigma_i^2\) の新しい値で状態空間システムの行列を更新するためのメソッドを作成します。
これを行うために、まずStatsmodelsで使用される一般的な状態空間表現が以下であることに注意してください。
そして、TVP-VAR(1) モデルは、以下の特殊化を意味します。
切片項はゼロです。つまり \(c_t = d_t = 0\) です。
デザイン行列 \(Z_t\) は時間変動しますが、その値は上記のように固定されています (つまり、その値には1と \(y_t\) のラグが含まれます)。
観測共分散行列は時間変動しません。つまり \(H_t = H_{t+1} = H\) です。
遷移行列は時間変動せず、単位行列に等しいです。つまり \(T_t = T_{t+1} = I\) です。
選択行列 \(R_t\) は時間変動せず、単位行列にも等しいです。つまり \(R_t = R_{t+1} = I\) です。
状態共分散行列 \(Q_t\) は時間変動せず、対角行列です。つまり \(Q_t = Q_{t+1} = \text{diag}(\{\sigma_i^2\})\) です。
[7]:
# 1. Create a new TVPVAR class as a subclass of sm.tsa.statespace.MLEModel
class TVPVAR(sm.tsa.statespace.MLEModel):
# Steps 2-3 are best done in the class "constructor", i.e. the __init__ method
def __init__(self, y):
# Create a matrix with [y_t' : y_{t-1}'] for t = 2, ..., T
augmented = sm.tsa.lagmat(y, 1, trim='both', original='in', use_pandas=True)
# Separate into y_t and z_t = [1 : y_{t-1}']
p = y.shape[1]
y_t = augmented.iloc[:, :p]
z_t = sm.add_constant(augmented.iloc[:, p:])
# Recall that the length of the state vector is p * (p + 1)
k_states = p * (p + 1)
super().__init__(y_t, exog=z_t, k_states=k_states)
# Note that the state space system matrices default to contain zeros,
# so we don't need to explicitly set c_t = d_t = 0.
# Construct the design matrix Z_t
# Notes:
# -> self.k_endog = p is the dimension of the observed vector
# -> self.k_states = p * (p + 1) is the dimension of the observed vector
# -> self.nobs = T is the number of observations in y_t
self['design'] = np.zeros((self.k_endog, self.k_states, self.nobs))
for i in range(self.k_endog):
start = i * (self.k_endog + 1)
end = start + self.k_endog + 1
self['design', i, start:end, :] = z_t.T
# Construct the transition matrix T = I
self['transition'] = np.eye(k_states)
# Construct the selection matrix R = I
self['selection'] = np.eye(k_states)
# Step 3: Initialize the state vector as alpha_1 ~ N(0, 5I)
self.ssm.initialize('known', stationary_cov=5 * np.eye(self.k_states))
# Step 4. Create a method that we can call to update H and Q
def update_variances(self, obs_cov, state_cov_diag):
self['obs_cov'] = obs_cov
self['state_cov'] = np.diag(state_cov_diag)
# Finally, it can be convenient to define human-readable names for
# each element of the state vector. These will be available in output
@property
def state_names(self):
state_names = np.empty((self.k_endog, self.k_endog + 1), dtype=object)
for i in range(self.k_endog):
endog_name = self.endog_names[i]
state_names[i] = (
['intercept.%s' % endog_name] +
['L1.%s->%s' % (other_name, endog_name) for other_name in self.endog_names])
return state_names.ravel().tolist()
上記のクラスは、任意のデータセットに対する状態空間モデルを定義しました。次に、実質GDP成長率、インフレ率、失業率、および金利を含む以前に作成したデータセットを使用して、その特定のインスタンスを作成する必要があります。
[8]:
# Create an instance of our TVPVAR class with our observed dataset y
mod = TVPVAR(y)
H, Q におけるアドホックなパラメータによる予備調査¶
以下の分析では、MCMCの反復をいくつかの初期パラメータ化から開始する必要があります。Chan and Jeliazkov (2009) に従い、\(H\) をデータセットのサンプル共分散行列に設定し、各 \(i\) に対して \(\sigma_i^2 = 0.01\) に設定します。
モデルに関する推論を可能にするMCMCスキームについて議論する前に、これらの初期パラメータを単純にプラグインした場合のモデルの出力を検討することができます。これらのパラメータを埋めるために、以前に定義した update_variances メソッドを使用し、それらのパラメータを条件としてカルマンフィルターとスムージングを実行します。
警告:この演習は説明に過ぎません。モデルの実際の意味を意味のある方法で研究するためには、MCMC演習の出力を待つ必要があります。.
[9]:
initial_obs_cov = np.cov(y.T)
initial_state_cov_diag = [0.01] * mod.k_states
# Update H and Q
mod.update_variances(initial_obs_cov, initial_state_cov_diag)
# Perform Kalman filtering and smoothing
# (the [] is just an empty list that in some models might contain
# additional parameters. Here, we don't have any additional parameters
# so we just pass an empty list)
initial_res = mod.smooth([])
initial_res 変数には、それらの初期パラメータを条件としたカルマンフィルターとスムージングの出力が含まれています。特に、\(E[\alpha_t \mid y^t, H, \{\sigma_i^2\}]\) である「平滑化された状態」に関心があるかもしれません。
まず、観測された変数の式に分離して、係数を時間経過でグラフ化する関数を作成しましょう。
[10]:
def plot_coefficients_by_equation(states):
fig, axes = plt.subplots(2, 2, figsize=(15, 8))
# The way we defined Z_t implies that the first 5 elements of the
# state vector correspond to the first variable in y_t, which is GDP growth
ax = axes[0, 0]
states.iloc[:, :5].plot(ax=ax)
ax.set_title('GDP growth')
ax.legend()
# The next 5 elements correspond to inflation
ax = axes[0, 1]
states.iloc[:, 5:10].plot(ax=ax)
ax.set_title('Inflation rate')
ax.legend();
# The next 5 elements correspond to unemployment
ax = axes[1, 0]
states.iloc[:, 10:15].plot(ax=ax)
ax.set_title('Unemployment equation')
ax.legend()
# The last 5 elements correspond to the interest rate
ax = axes[1, 1]
states.iloc[:, 15:20].plot(ax=ax)
ax.set_title('Interest rate equation')
ax.legend();
return ax
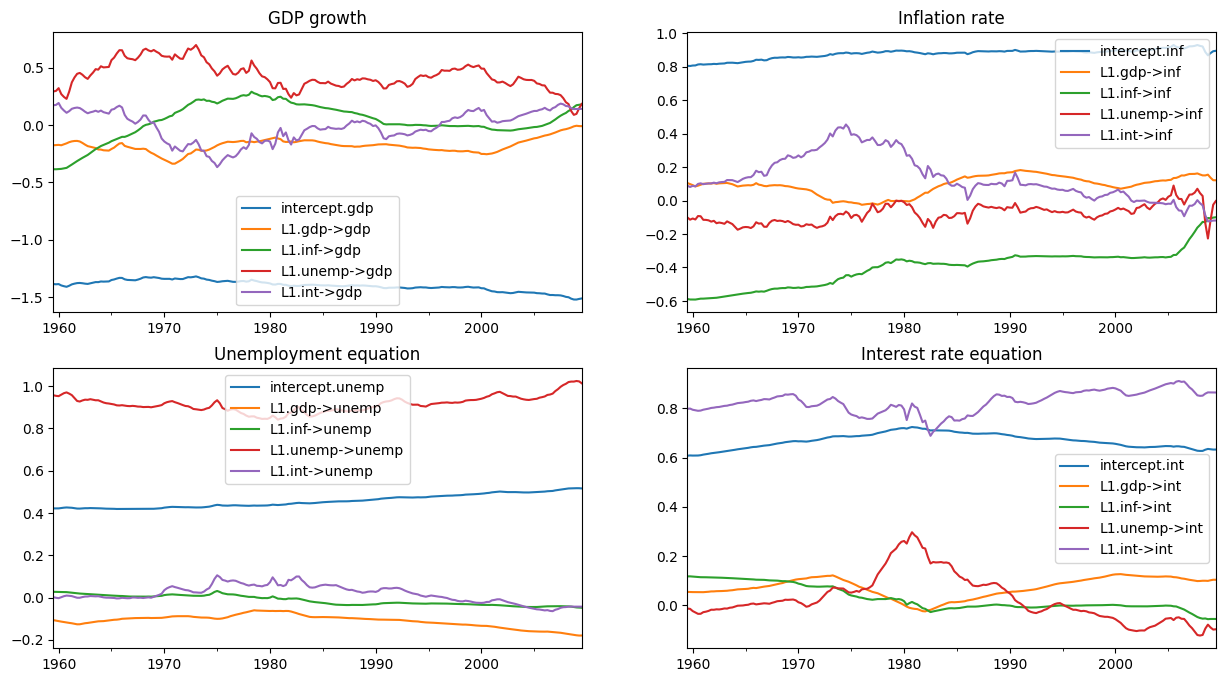
さて、結果オブジェクト initial_res の states.smoothed 属性で利用可能な平滑化された状態に関心があります。
下のグラフが示すように、初期パラメータ化は、一部の係数にかなりの時間変動があることを意味します。
[11]:
# Here, for illustration purposes only, we plot the time-varying
# coefficients conditional on an ad-hoc parameterization
# Recall that `initial_res` contains the Kalman filtering and smoothing,
# and the `states.smoothed` attribute contains the smoothed states
plot_coefficients_by_equation(initial_res.states.smoothed);
MCMCによるベイズ推定¶
次に、Chan and Jeliazkov (2009) のアルゴリズム 2 で説明されているギブスサンプラー方式を実装します。
以下の (条件付きで共役な) 事前分布を使用します。
ここで、\(\mathcal{IW}\) は逆ウィシャート分布を表し、\(\mathcal{IG}\) は逆ガンマ分布を表します。事前分布のハイパーパラメータは次のように設定します。
[12]:
# Prior hyperparameters
# Prior for obs. cov. is inverse-Wishart(v_1^0=k + 3, S10=I)
v10 = mod.k_endog + 3
S10 = np.eye(mod.k_endog)
# Prior for state cov. variances is inverse-Gamma(v_{i2}^0 / 2 = 3, S+{i2}^0 / 2 = 0.005)
vi20 = 6
Si20 = 0.01
MCMCの反復を実行する前に、いくつかの実際的なステップがあります。
状態ベクトル、観測共分散行列、および状態誤差分散のドローを格納するための配列を作成します。
HとQの初期値 (上記で説明) をストレージベクトルに入れます。
状態ベクトルのドローを作成するために、
TVPVARインスタンスに関連付けられたシミュレーション・スムーザーオブジェクトを構築します。
[13]:
# Gibbs sampler setup
niter = 11000
nburn = 1000
# 1. Create storage arrays
store_states = np.zeros((niter + 1, mod.nobs, mod.k_states))
store_obs_cov = np.zeros((niter + 1, mod.k_endog, mod.k_endog))
store_state_cov = np.zeros((niter + 1, mod.k_states))
# 2. Put in the initial values
store_obs_cov[0] = initial_obs_cov
store_state_cov[0] = initial_state_cov_diag
mod.update_variances(store_obs_cov[0], store_state_cov[0])
# 3. Construct posterior samplers
sim = mod.simulation_smoother(method='cfa')
以前と同様に、カルマンフィルターとスムーザーに基づくシミュレーション・スムーザー、またはコレスキー分解アルゴリズムに基づくシミュレーション・スムーザーのいずれかを使用できます。
[14]:
for i in range(niter):
mod.update_variances(store_obs_cov[i], store_state_cov[i])
sim.simulate()
# 1. Sample states
store_states[i + 1] = sim.simulated_state.T
# 2. Simulate obs cov
fitted = np.matmul(mod['design'].transpose(2, 0, 1), store_states[i + 1][..., None])[..., 0]
resid = mod.endog - fitted
store_obs_cov[i + 1] = invwishart.rvs(v10 + mod.nobs, S10 + resid.T @ resid)
# 3. Simulate state cov variances
resid = store_states[i + 1, 1:] - store_states[i + 1, :-1]
sse = np.sum(resid**2, axis=0)
for j in range(mod.k_states):
rv = invgamma.rvs((vi20 + mod.nobs - 1) / 2, scale=(Si20 + sse[j]) / 2)
store_state_cov[i + 1, j] = rv
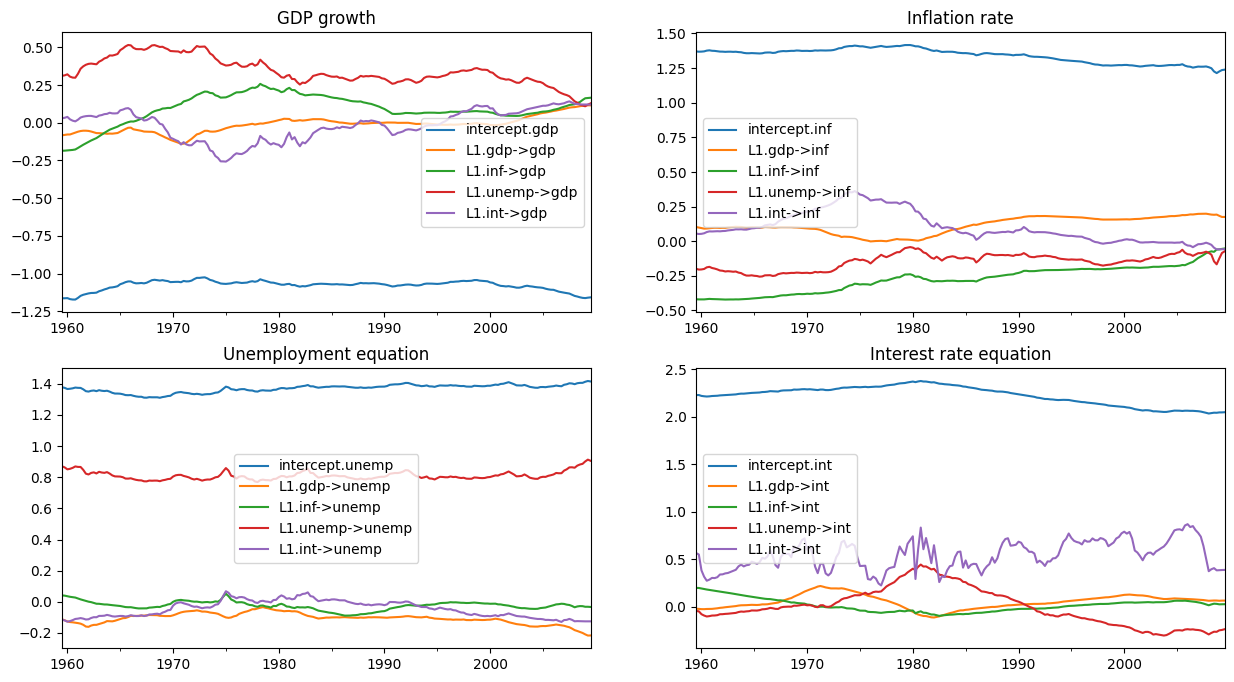
初期のドローをいくつか削除した後、事後分布からの残りのドローを使用すると、推論を実行できます。以下に、時間変動回帰係数の事後平均をプロットします。
(注: これらのプロットは、Chan and Jeliazkov (2009) の公開版の図 1 とは異なりますが、http://joshuachan.org/code/code_TVPVAR.html で入手可能なMatlab複製コードで生成されたものと非常によく似ています)
[15]:
# Collect the posterior means of each time-varying coefficient
states_posterior_mean = pd.DataFrame(
np.mean(store_states[nburn + 1:], axis=0),
index=mod._index, columns=mod.state_names)
# Plot these means over time
plot_coefficients_by_equation(states_posterior_mean);
Pythonには、ベイズモデルの探索を支援するためのライブラリも多数あります。ここでは、arviz パッケージを使用して、各共分散および分散パラメータの信用区間を探索するだけですが、分析のためのはるかに幅広いツールセットが利用可能です。
[16]:
import arviz as az
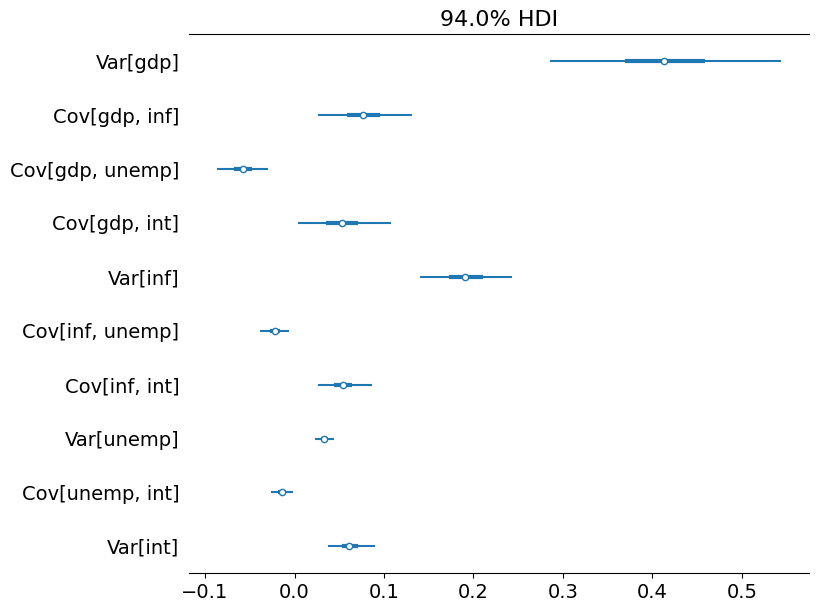
# Collect the observation error covariance parameters
az_obs_cov = az.convert_to_inference_data({
('Var[%s]' % mod.endog_names[i] if i == j else
'Cov[%s, %s]' % (mod.endog_names[i], mod.endog_names[j])):
store_obs_cov[nburn + 1:, i, j]
for i in range(mod.k_endog) for j in range(i, mod.k_endog)})
# Plot the credible intervals
az.plot_forest(az_obs_cov, figsize=(8, 7));
[17]:
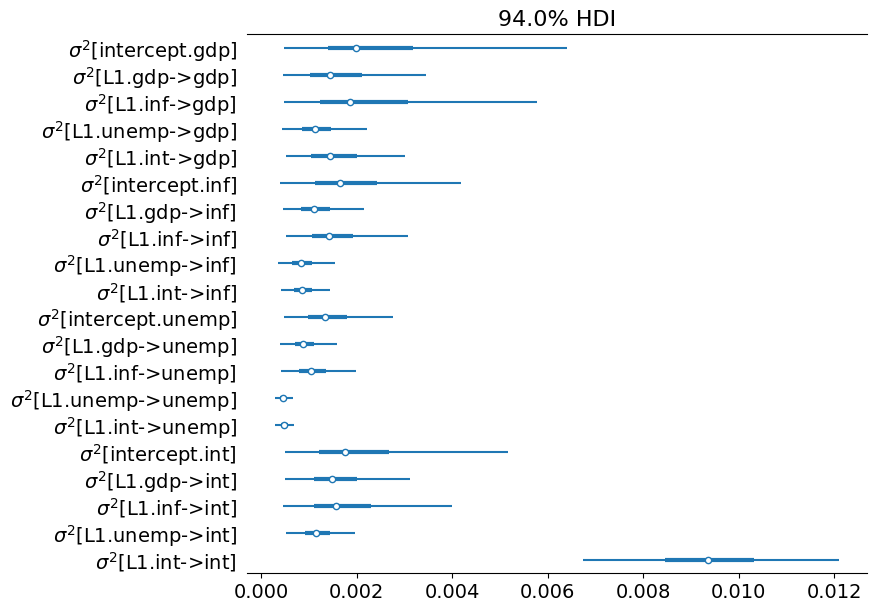
# Collect the state innovation variance parameters
az_state_cov = az.convert_to_inference_data({
r'$\sigma^2$[%s]' % mod.state_names[i]: store_state_cov[nburn + 1:, i]
for i in range(mod.k_states)})
# Plot the credible intervals
az.plot_forest(az_state_cov, figsize=(8, 7));
付録: パフォーマンス¶
最後に、%timeit Jupyter Notebookマジックを使用して、KFSとCFAのシミュレーション・スムーザーのパフォーマンスを比較するための簡単なテストをいくつか実行します。
1つの注意点は、KFSシミュレーション・スムーザーは、事後状態ベクトルのシミュレーションだけでなく、さまざまな出力を生成する可能性があり、これらの追加の計算が結果を偏らせる可能性があることです。結果を比較可能にするために、simulation_output 引数を使用して、状態のシミュレーションのみを計算するようにKFSシミュレーション・スムーザーに指示します。
[18]:
from statsmodels.tsa.statespace.simulation_smoother import SIMULATION_STATE
sim_cfa = mod.simulation_smoother(method='cfa')
sim_kfs = mod.simulation_smoother(simulation_output=SIMULATION_STATE)
次に、以下のコードを使用して、基本的なタイミング演習を実行できます。
%timeit -n 10000 -r 3 sim_cfa.simulate()
%timeit -n 10000 -r 3 sim_kfs.simulate()
これをテストしたマシンでは、次のような結果になりました。
2.06 ms ± 26.5 µs per loop (mean ± std. dev. of 3 runs, 10000 loops each)
2.02 ms ± 68.4 µs per loop (mean ± std. dev. of 3 runs, 10000 loops each)
これらの結果は、少なくともこのモデルでは、KFSアプローチと比較して、CFAアプローチによる計算上の顕著な利点はないことを示唆しています。ただし、これは次のことを除外するものではありません。
CFAシミュレーション・スムーザーのStatsmodels実装は、さらに最適化される可能性があります。
CFAアプローチは、特定のモデル (たとえば、多数の
endog変数を持つモデル) に対してのみ改善を示す可能性があります。
最初の可能性を評価するための最初の簡単な方法は、CFAシミュレーション・スムーザーのStatsmodels実装の実行時間を、Chan and Jeliazkov (2009) の複製コードのMatlab実装 ( http://joshuachan.org/code/code_TVPVAR.html で入手可能) と比較することです。
CFAシミュレーション・スムーザーのStatsmodelsバージョンはCythonで記述され、Cコードにコンパイルされますが、MatlabバージョンはMatlabのスパース行列機能を利用しています。その結果、コンパイルされたコードではありませんが、比較的優れたパフォーマンスが得られると予想できます。
これをテストしたマシンでは、Matlabバージョンは通常、11,000回の反復でMCMCループを70〜75秒で実行しましたが、このノートブックのStatsmodels CFAシミュレーション・スムーザーを使用したMCMCループ (上記参照) は、11,000回の反復で40〜45秒で実行しました。これは、CFAスムーザーのStatsmodels実装がすでに比較的うまく機能しているといういくつかの証拠です (ただし、追加の改善の余地がないわけではありません)。
参考文献¶
Carter, Chris K., and Robert Kohn. “On Gibbs sampling for state space models.” Biometrika 81, no. 3 (1994): 541-553.
Chan, Joshua CC, and Ivan Jeliazkov. “Efficient simulation and integrated likelihood estimation in state space models.” International Journal of Mathematical Modelling and Numerical Optimisation 1, no. 1-2 (2009): 101-120.
De Jong, Piet, and Neil Shephard. “The simulation smoother for time series models.” Biometrika 82, no. 2 (1995): 339-350.
Durbin, James, and Siem Jan Koopman. “A simple and efficient simulation smoother for state space time series analysis.” Biometrika 89, no. 3 (2002): 603-616.
McCausland, William J., Shirley Miller, and Denis Pelletier. “Simulation smoothing for state–space models: A computational efficiency analysis.” Computational Statistics & Data Analysis 55, no. 1 (2011): 199-212.