SARIMAXとARIMA：よくある質問（FAQ）¶
このノートブックには、よくある質問の説明が含まれています。
`SARIMAX`、`ARIMA`、および`AutoReg`におけるトレンドと外生変数の比較
`SARIMAX`と`ARIMA`における残差、適合値、および予測の再構築
`SARIMAX`と`ARIMA`における初期残差
`SARIMAX`、`ARIMA`、および`AutoReg`におけるトレンドと外生変数の比較¶
`ARIMA`は、正式にはARMA誤差を持つOLSです。ARMA誤差を持つOLSにおける基本的なAR（1）は、次のように記述されます。
\[\begin{split}\begin{align} Y_t & = \delta + \epsilon_t \\ \epsilon_t & = \rho \epsilon_{t-1} + \eta_t \\ \eta_t & \sim WN(0,\sigma^2) \\ \end{align}\end{split}\]
大標本では、\(\hat{\delta}\stackrel{p}{\rightarrow} E[Y]\)です。
`SARIMAX`は異なる表現を使用するため、`SARIMAX`を使用して推定されるモデルは次のようになります。
\[\begin{split}\begin{align} Y_t & = \phi + \rho Y_{t-1} + \eta_t \\ \eta_t & \sim WN(0,\sigma^2) \\ \end{align}\end{split}\]
これは、モデルがOLS（`AutoReg`）を使用して推定される場合に使用されるのと同じ表現です。大標本では、\(\hat{\phi}\stackrel{p}{\rightarrow} E[Y](1-\rho)\)です。
次のセルでは、大標本をシミュレートし、これらの関係が実際に成立することを確認します。
[1]:
%matplotlib inline
[2]:
import numpy as np
import pandas as pd
rng = np.random.default_rng(20210819)
eta = rng.standard_normal(5200)
rho = 0.8
beta = 10
epsilon = eta.copy()
for i in range(1, eta.shape[0]):
epsilon[i] = rho * epsilon[i - 1] + eta[i]
y = beta + epsilon
y = y[200:]
[3]:
from statsmodels.tsa.api import SARIMAX, AutoReg
from statsmodels.tsa.arima.model import ARIMA
3つのモデルは、次のセルで指定および推定されます。AR（0）は参照として含まれています。AR（0）は、3つのすべての推定量を使用して同一です。
[4]:
ar0_res = SARIMAX(y, order=(0, 0, 0), trend="c").fit()
sarimax_res = SARIMAX(y, order=(1, 0, 0), trend="c").fit()
arima_res = ARIMA(y, order=(1, 0, 0), trend="c").fit()
autoreg_res = AutoReg(y, 1, trend="c").fit()
This problem is unconstrained.
This problem is unconstrained.
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 2 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 1.91760D+00 |proj g|= 3.68860D-06
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
2 0 1 0 0 0 3.689D-06 1.918D+00
F = 1.9175996129577773
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 3 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 1.41373D+00 |proj g|= 9.51828D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
3 2 5 1 0 0 4.516D-05 1.414D+00
F = 1.4137311050015484
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
以下の表には、モデルの推定パラメータ、推定AR（1）係数、および推定パラメータ（AR（0）または`ARIMA`）に等しいか、切片と1からAR（1）パラメータを引いた値の比率に依存する長期平均が含まれています。
[5]:
intercept = [
ar0_res.params[0],
sarimax_res.params[0],
arima_res.params[0],
autoreg_res.params[0],
]
rho_hat = [0] + [r.params[1] for r in (sarimax_res, arima_res, autoreg_res)]
long_run = [
ar0_res.params[0],
sarimax_res.params[0] / (1 - sarimax_res.params[1]),
arima_res.params[0],
autoreg_res.params[0] / (1 - autoreg_res.params[1]),
]
cols = ["AR(0)", "SARIMAX", "ARIMA", "AutoReg"]
pd.DataFrame(
[intercept, rho_hat, long_run],
columns=cols,
index=["delta-or-phi", "rho", "long-run mean"],
)
[5]:
| AR(0) | SARIMAX | ARIMA | AutoReg | |
|---|---|---|---|---|
| deltaまたはphi | 9.7745 | 1.985714 | 9.774498 | 1.985790 |
| rho | 0.0000 | 0.796846 | 0.796875 | 0.796882 |
| 長期平均 | 9.7745 | 9.774424 | 9.774498 | 9.776537 |
`SARIMAX`におけるトレンドとexogの違い¶
`SARIMAX`に`exog`変数が含まれる場合、`exog`はOLS回帰変数として扱われるため、推定されるモデルは次のようになります。
\[\begin{split}\begin{align} Y_t - X_t \beta & = \delta + \rho (Y_{t-1} - X_{t-1}\beta) + \eta_t \\ \eta_t & \sim WN(0,\sigma^2) \\ \end{align}\end{split}\]
次の例では、トレンドを省略し、代わりに1の列を含めます。これにより、大標本では、外生回帰変数がない場合と`trend="c"`の場合と同等のモデルが生成されます。ここで、`const`の推定値は、`ARIMA`を使用して推定された値と一致します。これは、`SARIMAX`のexogと`ARIMA`のトレンドの両方が、ARMA誤差を持つ線形回帰モデルとして扱われるためです。
[6]:
sarimax_exog_res = SARIMAX(y, exog=np.ones_like(y), order=(1, 0, 0), trend="n").fit()
print(sarimax_exog_res.summary())
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 3 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 1.41373D+00 |proj g|= 1.06920D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
3 1 4 1 0 0 4.752D-05 1.414D+00
F = 1.4137311099487531
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
This problem is unconstrained.
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 5000
Model: SARIMAX(1, 0, 0) Log Likelihood -7068.656
Date: Thu, 03 Oct 2024 AIC 14143.311
Time: 15:45:04 BIC 14162.863
Sample: 0 HQIC 14150.164
- 5000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 9.7745 0.069 141.177 0.000 9.639 9.910
ar.L1 0.7969 0.009 93.691 0.000 0.780 0.814
sigma2 0.9894 0.020 49.921 0.000 0.951 1.028
===================================================================================
Ljung-Box (L1) (Q): 0.42 Jarque-Bera (JB): 0.08
Prob(Q): 0.51 Prob(JB): 0.96
Heteroskedasticity (H): 0.97 Skew: -0.01
Prob(H) (two-sided): 0.47 Kurtosis: 2.99
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
`SARIMAX`と`ARIMA`における`exog`の使用¶
`exog`は両方のモデルで同じように扱われますが、切片は引き続き異なります。以下では、`y`に外生回帰変数を追加し、3つのすべての方法を使用してモデルを適合させます。データ生成プロセスは次のようになります。
\[\begin{split}\begin{align} Y_t & = \delta + X_t \beta + \epsilon_t \\ \epsilon_t & = \rho \epsilon_{t-1} + \eta_t \\ \eta_t & \sim WN(0,\sigma^2) \\ \end{align}\end{split}\]
[7]:
full_x = rng.standard_normal(eta.shape)
x = full_x[200:]
y += 3 * x
[8]:
sarimax_exog_res = SARIMAX(y, exog=x, order=(1, 0, 0), trend="c").fit()
arima_exog_res = ARIMA(y, exog=x, order=(1, 0, 0), trend="c").fit()
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 4 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 1.42683D+00 |proj g|= 2.05943D-01
This problem is unconstrained.
At iterate 5 f= 1.41332D+00 |proj g|= 1.60874D-03
At iterate 10 f= 1.41329D+00 |proj g|= 3.11659D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
4 11 15 1 0 0 1.796D-06 1.413D+00
F = 1.4132928400115858
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
パラメータテーブルを調べると、`x1`のパラメータ推定値は同一ですが、これらの推定量におけるトレンドの処理の違いにより、`intercept`の推定値は引き続き異なります。
`SARIMAX`¶
[9]:
def print_params(s):
from io import StringIO
return pd.read_csv(StringIO(s.tables[1].as_csv()), index_col=0)
print_params(sarimax_exog_res.summary())
[9]:
| 係数 | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 切片 | 1.9849 | 0.085 | 23.484 | 0.0 | 1.819 | 2.151 |
| x1 | 3.0231 | 0.011 | 277.150 | 0.0 | 3.002 | 3.044 |
| ar.L1 | 0.7969 | 0.009 | 93.735 | 0.0 | 0.780 | 0.814 |
| sigma2 | 0.9886 | 0.020 | 49.941 | 0.0 | 0.950 | 1.027 |
`ARIMA`¶
[10]:
print_params(arima_exog_res.summary())
[10]:
| 係数 | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 定数 | 9.7741 | 0.069 | 141.201 | 0.0 | 9.638 | 9.910 |
| x1 | 3.0231 | 0.011 | 277.140 | 0.0 | 3.002 | 3.044 |
| ar.L1 | 0.7969 | 0.009 | 93.728 | 0.0 | 0.780 | 0.814 |
| sigma2 | 0.9886 | 0.020 | 49.941 | 0.0 | 0.950 | 1.027 |
`AutoReg`における`exog`¶
`AutoReg`を使用してOLSでモデルを推定する場合、モデルは`SARIMAX`と`ARIMA`の両方とは異なります。外生変数を持つ`AutoReg`の仕様は次のとおりです。
\[\begin{split}\begin{align} Y_t & = \phi + \rho Y_{t-1} + X_{t}\beta + \eta_t \\ \eta_t & \sim WN(0,\sigma^2) \\ \end{align}\end{split}\]
この仕様は、`SARIMAX`と`ARIMA`で推定される仕様と同等ではありません。ここで、違いは些細なものではなく、同じ時系列に対する単純な推定では、大標本（および極限）であっても異なるパラメータ値が得られます。このモデルを推定すると、AR（1）係数のパラメータ推定値が変更されます。
`AutoReg`¶
[11]:
autoreg_exog_res = AutoReg(y, 1, exog=x, trend="c").fit()
print_params(autoreg_exog_res.summary())
[11]:
| 係数 | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 定数 | 7.9714 | 0.064 | 124.525 | 0.0 | 7.846 | 8.097 |
| y.L1 | 0.1838 | 0.006 | 29.890 | 0.0 | 0.172 | 0.196 |
| x1 | 3.0311 | 0.021 | 142.513 | 0.0 | 2.989 | 3.073 |
重要な違いは、モデルをラグ演算子表記で記述することでわかります。
\[\begin{split}\begin{align} (1-\phi L ) Y_t & = X_{t}\beta + \eta_t \Rightarrow \\ Y_t & = (1-\phi L )^{-1}\left(X_{t}\beta + \eta_t\right) \\ Y_t & = \sum_{i=0}^{\infty} \phi^i \left(X_{t-i}\beta + \eta_{t-i}\right) \end{align}\end{split}\]
ここで、\(|\phi|<1\)と仮定します。ここで、\(Y_t\)は\(X_t\)と\(\eta_t\)のすべてのラグ値に依存することがわかります。これは、`SARIMAX`と`ARIMA`で推定される仕様とは異なり、次のように表すことができます。
\[\begin{split}\begin{align} Y_t - X_t \beta & = \delta + \rho (Y_{t-1} - X_{t-1}\beta) + \eta_t \\ \left(1-\rho L \right)\left(Y_t - X_t \beta\right) & = \delta + \eta_t \\ Y_t - X_t \beta & = \frac{\delta}{1-\rho} + \left(1-\rho L \right)^{-1}\eta_t \\ Y_t - X_t \beta & = \frac{\delta}{1-\rho} + \sum_{i=0}^\infty \rho^i \eta_{t-i} \\ Y_t & = \frac{\delta}{1-\rho} + X_t \beta + \sum_{i=0}^\infty \rho^i \eta_{t-i} \\ \end{align}\end{split}\]
この仕様では、\(Y_t\)は\(X_t\)のみに依存し、他のラグには依存しません。
`AutoReg`で正しいDGPを使用する¶
`AutoReg`で推定されるプロセスをシミュレートすると、パラメータが真のモデルから回復されることがわかります。
[12]:
y = beta + eta
epsilon = eta.copy()
for i in range(1, eta.shape[0]):
y[i] = beta * (1 - rho) + rho * y[i - 1] + 3 * full_x[i] + eta[i]
y = y[200:]
正しいDGPを使用した`AutoReg`¶
[13]:
autoreg_alt_exog_res = AutoReg(y, 1, exog=x, trend="c").fit()
print_params(autoreg_alt_exog_res.summary())
[13]:
| 係数 | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 定数 | 1.9870 | 0.030 | 66.526 | 0.0 | 1.928 | 2.046 |
| y.L1 | 0.7968 | 0.003 | 300.382 | 0.0 | 0.792 | 0.802 |
| x1 | 3.0263 | 0.014 | 217.034 | 0.0 | 2.999 | 3.054 |
`SARIMAX`と`ARIMA`における残差、適合値、および予測の再構築¶
自己回帰項、トレンド、および外生変数のみを含むモデルでは、モデルの最大ラグ長に達すると、適合値と予測値を簡単に再構築できます。実際には、これは \((P+D)s+p+d\) 期間後を意味します。モデルは \(Y_t|Y_{t-1},Y_{t-2},...\) に対する最良の予測を構築するため、それ以前の予測と残差は再構築がより困難です。\(Y\) のラグ数が自己回帰次数より少ない場合、最適予測の式はモデルと異なります。たとえば、最初の値 \(Y_1\) を予測する場合、\(Y\) の履歴から利用できる情報がないため、最良の予測は無条件平均です。AR(1) の場合、2 番目の予測はモデルに従います。そのため、ARIMA を使用する場合、予測は次のようになります。
\[Y_2 = \hat{\delta} + \hat{\rho} \left(Y_1 - \hat{\delta}\right)\]
ARIMA は外生項とトレンド項の両方を ARMA 誤差を持つ回帰として扱うためです。
これは、次のセルのセットで確認できます。
[14]:
arima_res = ARIMA(y, order=(1, 0, 0), trend="c").fit()
print_params(arima_res.summary())
[14]:
| 係数 | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 定数 | 9.9346 | 0.222 | 44.667 | 0.0 | 9.499 | 10.371 |
| ar.L1 | 0.7957 | 0.009 | 92.515 | 0.0 | 0.779 | 0.813 |
| sigma2 | 10.3015 | 0.204 | 50.496 | 0.0 | 9.902 | 10.701 |
[15]:
arima_res.predict(0, 2)
[15]:
array([ 9.93458658, 10.91088035, 11.80415747])
[16]:
delta_hat, rho_hat = arima_res.params[:2]
delta_hat + rho_hat * (y[0] - delta_hat)
[16]:
np.float64(10.910880346250012)
SARIMAX はトレンド項を異なる方法で処理するため、SARIMAX を使用して推定されたモデルからの 1 ステップ予測は次のようになります。
\[Y_2 = \hat\delta + \hat\rho Y_1\]
[17]:
sarima_res = SARIMAX(y, order=(1, 0, 0), trend="c").fit()
print_params(sarima_res.summary())
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 3 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 2.58518D+00 |proj g|= 5.99456D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
3 3 5 1 0 0 3.347D-05 2.585D+00
F = 2.5851830060985752
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
This problem is unconstrained.
[17]:
| 係数 | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 切片 | 2.0283 | 0.097 | 20.841 | 0.0 | 1.838 | 2.219 |
| ar.L1 | 0.7959 | 0.009 | 92.536 | 0.0 | 0.779 | 0.813 |
| sigma2 | 10.3007 | 0.204 | 50.500 | 0.0 | 9.901 | 10.700 |
[18]:
sarima_res.predict(0, 2)
[18]:
array([ 9.93588659, 10.91128867, 11.80469658])
[19]:
delta_hat, rho_hat = sarima_res.params[:2]
delta_hat + rho_hat * y[0]
[19]:
np.float64(10.911288670367867)
MA 成分を含む予測¶
モデルに MA 成分が含まれている場合、誤差は直接観測できないため、予測はより複雑になります。予測は依然として \(Y_t|Y_{t-1},Y_{t-2},...\) であり、MA 成分が反転可能な場合、最適予測は \(t\)-ラグ AR プロセスとして表すことができます。\(t\) が大きい場合、これは誤差が観測可能である場合の予測と非常に近くなります。短いラグの場合、これは大きく異なる可能性があります。
次のセルでは、MA(1) プロセスをシミュレートし、MA モデルを適合させます。
[20]:
rho = 0.8
beta = 10
epsilon = eta.copy()
for i in range(1, eta.shape[0]):
epsilon[i] = rho * eta[i - 1] + eta[i]
y = beta + epsilon
y = y[200:]
ma_res = ARIMA(y, order=(0, 0, 1), trend="c").fit()
print_params(ma_res.summary())
[20]:
| 係数 | 標準誤差 | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| 定数 | 9.9185 | 0.025 | 391.129 | 0.0 | 9.869 | 9.968 |
| ma.L1 | 0.8025 | 0.009 | 93.864 | 0.0 | 0.786 | 0.819 |
| sigma2 | 0.9904 | 0.020 | 49.925 | 0.0 | 0.951 | 1.029 |
まず、サンプルの開始付近の予測、y[1]、…、y[5] に対応する予測を見てみましょう。
[21]:
ma_res.predict(1, 5)
[21]:
array([ 8.57011015, 9.19907188, 8.96971353, 9.78987115, 11.11984478])
そして、「直接」予測を生成するために必要な対応する残差は次のとおりです。
[22]:
ma_res.resid[:5]
[22]:
array([-2.7621904 , -1.12255005, -1.33557621, -0.17206944, 1.5634041 ])
モデルパラメータを使用して、MA(1) 仕様を使用して「直接」予測を生成できます。
\[\hat Y_t = \hat\delta + \hat\rho \hat\epsilon_{t-1}\]
これらは初期予測の実際のモデル予測に特に近いわけではありませんが、ギャップは急速に縮小することがわかります。
[23]:
delta_hat, rho_hat = ma_res.params[:2]
direct = delta_hat + rho_hat * ma_res.resid[:5]
direct
[23]:
array([ 7.70168405, 9.01756049, 8.84659855, 9.7803589 , 11.17314527])
差は最初の予測ではほぼ標準偏差ですが、インデックスが増加するにつれて減少します。
[24]:
ma_res.predict(1, 5) - direct
[24]:
array([ 0.8684261 , 0.18151139, 0.12311499, 0.00951225, -0.05330049])
次に、サンプルの終わりと最後の 3 つの予測を見てみましょう。
[25]:
t = y.shape[0]
ma_res.predict(t - 3, t - 1)
[25]:
array([ 9.79692804, 10.51272714, 10.55855562])
[26]:
ma_res.resid[-4:-1]
[26]:
array([-0.15142355, 0.74049384, 0.79759816])
[27]:
direct = delta_hat + rho_hat * ma_res.resid[-4:-1]
direct
[27]:
array([ 9.79692804, 10.51272714, 10.55855562])
「直接」予測は同一です。これは、短いサンプルの影響がサンプルの終わりまでに消えるためです（実際には、観測値 100 程度までに無視できる程度になり、観測値 160 程度までに数値的にはなくなります）。
[28]:
ma_res.predict(t - 3, t - 1) - direct
[28]:
array([0., 0., 0.])
同じ原則は、複数のラグまたは季節項を含むより複雑なモデルにも適用されます。AR モデルの予測は、有効なラグ長に達すると単純になりますが、MA 成分を含むモデルの予測は、MA ラグ多項式の最大根が十分に小さくなり、残差が真の残差に近くなった場合にのみ単純になります。
SARIMAX と ARIMA の予測の違い¶
SARIMAX モデルと ARIMA モデルから予測を行うために使用される式は、1 つの重要な点で異なります。ARIMA は、切片や時間トレンドなど、すべてのトレンド項を外生回帰変数の一部として扱います。たとえば、ARIMA を使用して推定された、切片と線形時間トレンドを持つ AR(1) モデルの仕様は次のとおりです。
\[\begin{split}\begin{align*} Y_t - \delta_0 - \delta_1 t & = \epsilon_t \\ \epsilon_t & = \rho \epsilon_{t-1} + \eta_t \end{align*}\end{split}\]
同じモデルを SARIMAX を使用して推定する場合、仕様は次のようになります。
\[\begin{split}\begin{align*} Y_t & = \epsilon_t \\ \epsilon_t & = \delta_0 + \delta_1 t + \rho \epsilon_{t-1} + \eta_t \end{align*}\end{split}\]
モデルに外生回帰変数 \(X_t\) が含まれている場合、違いはより顕著になります。ARIMA の仕様は次のとおりです。
\[\begin{split}\begin{align*} Y_t - \delta_0 - \delta_1 t - X_t \beta & = \epsilon_t \\ \epsilon_t & = \rho \epsilon_{t-1} + \eta_t \\ & = \rho \left(Y_{t-1} - \delta_0 - \delta_1 (t-1) - X_{t-1} \beta\right) + \eta_t \end{align*}\end{split}\]
SARIMAX の仕様は次のとおりです。
\[\begin{split}\begin{align*} Y_t & = X_t \beta + \epsilon_t \\ \epsilon_t & = \delta_0 + \delta_1 t + \rho \epsilon_{t-1} + \eta_t \\ & = \delta_0 + \delta_1 t + \rho \left(Y_{t-1} - X_{t-1}\beta\right) + \eta_t \end{align*}\end{split}\]
これら 2 つの主な違いは、切片とトレンドは ARIMA では外生回帰と事実上同等ですが、SARIMAX では標準の ARMA 項に似ていることです。
次のセルでは、ARIMA の仕様を使用して時間トレンドを持つ ARX をシミュレートし、両方の推定量を使用してパラメータを推定します。
[29]:
rho = 0.8
beta = 2
delta0 = 10
delta1 = 0.5
epsilon = eta.copy()
for i in range(1, eta.shape[0]):
epsilon[i] = rho * epsilon[i - 1] + eta[i]
t = np.arange(epsilon.shape[0])
y = delta0 + delta1 * t + beta * full_x + epsilon
y = y[200:]
[30]:
start = np.array([110, delta1, beta, rho, 1])
arx_res = ARIMA(y, exog=x, order=(1, 0, 0), trend="ct").fit()
mod = SARIMAX(y, exog=x, order=(1, 0, 0), trend="ct")
start[:2] *= 1 - rho
sarimax_res = mod.fit(start_params=start, method="bfgs")
Current function value: 1.413691
Iterations: 43
Function evaluations: 72
Gradient evaluations: 62
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/scipy/optimize/_optimize.py:1291: OptimizeWarning: Desired error not necessarily achieved due to precision loss.
res = _minimize_bfgs(f, x0, args, fprime, callback=callback, **opts)
/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/base/model.py:607: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
warnings.warn("Maximum Likelihood optimization failed to "
2 つの推定量は同様に適合しますが、対数尤度にわずかな違いがあります。これは数値的な問題であり、予測に重大な影響を与えるべきではありません。重要なのは、2 つのトレンドパラメータ、const と x1 (残念ながら時間トレンドの名前が付けられています) が、2 つの推定量で異なっていることです。他のパラメータは事実上同一です。
[31]:
print(arx_res.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 5000
Model: ARIMA(1, 0, 0) Log Likelihood -7069.171
Date: Thu, 03 Oct 2024 AIC 14148.343
Time: 15:45:16 BIC 14180.928
Sample: 0 HQIC 14159.763
- 5000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 109.2112 0.137 796.186 0.000 108.942 109.480
x1 0.5000 4.78e-05 1.05e+04 0.000 0.500 0.500
x2 2.0495 0.011 187.517 0.000 2.028 2.071
ar.L1 0.7965 0.009 93.669 0.000 0.780 0.813
sigma2 0.9897 0.020 49.854 0.000 0.951 1.029
===================================================================================
Ljung-Box (L1) (Q): 0.33 Jarque-Bera (JB): 0.15
Prob(Q): 0.57 Prob(JB): 0.93
Heteroskedasticity (H): 0.97 Skew: -0.01
Prob(H) (two-sided): 0.53 Kurtosis: 3.00
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
[32]:
print(sarimax_res.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 5000
Model: SARIMAX(1, 0, 0) Log Likelihood -7068.457
Date: Thu, 03 Oct 2024 AIC 14146.914
Time: 15:45:16 BIC 14179.500
Sample: 0 HQIC 14158.335
- 5000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 22.7438 0.929 24.481 0.000 20.923 24.565
drift 0.1019 0.004 23.985 0.000 0.094 0.110
x1 2.0230 0.011 185.290 0.000 2.002 2.044
ar.L1 0.7963 0.008 93.745 0.000 0.780 0.813
sigma2 0.9894 0.020 49.899 0.000 0.951 1.028
===================================================================================
Ljung-Box (L1) (Q): 0.47 Jarque-Bera (JB): 0.13
Prob(Q): 0.49 Prob(JB): 0.94
Heteroskedasticity (H): 0.97 Skew: -0.01
Prob(H) (two-sided): 0.47 Kurtosis: 3.00
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
初期残差 SARIMAX と ARIMA¶
AR、MA、季節 AR、季節 MA、および差分パラメータに依存する最大モデル次数より前の観測値の残差は信頼性が低く、パフォーマンス評価に使用しないでください。一般に、次数 \((p,d,q)\times(P,D,Q,s)\) の ARIMA では、精度が低い残差の式は次のとおりです。
\[\max((P+D)s+p+d,Qs+q)\]
ARIMA(1,0,0)(1,0,0,12) からいくつかのデータをシミュレートし、残差を調べることができます。
[33]:
import numpy as np
import pandas as pd
rho = 0.8
psi = -0.6
beta = 20
epsilon = eta.copy()
for i in range(13, eta.shape[0]):
epsilon[i] = (
rho * epsilon[i - 1]
+ psi * epsilon[i - 12]
- (rho * psi) * epsilon[i - 13]
+ eta[i]
)
y = beta + epsilon
y = y[200:]
サンプルが大きい場合、パラメータ推定値は DGP パラメータと非常に近くなります。
[34]:
res = ARIMA(y, order=(1, 0, 0), trend="c", seasonal_order=(1, 0, 0, 12)).fit()
print(res.summary())
SARIMAX Results
========================================================================================
Dep. Variable: y No. Observations: 5000
Model: ARIMA(1, 0, 0)x(1, 0, 0, 12) Log Likelihood -7076.266
Date: Thu, 03 Oct 2024 AIC 14160.532
Time: 15:45:19 BIC 14186.600
Sample: 0 HQIC 14169.668
- 5000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 19.8586 0.043 458.609 0.000 19.774 19.943
ar.L1 0.7972 0.008 93.925 0.000 0.781 0.814
ar.S.L12 -0.6044 0.011 -53.280 0.000 -0.627 -0.582
sigma2 0.9914 0.020 49.899 0.000 0.952 1.030
===================================================================================
Ljung-Box (L1) (Q): 0.50 Jarque-Bera (JB): 0.11
Prob(Q): 0.48 Prob(JB): 0.95
Heteroskedasticity (H): 0.96 Skew: -0.01
Prob(H) (two-sided): 0.40 Kurtosis: 2.99
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
まず、最初の 13 個の残差をモデルの実際のショックに対してプロットすることで調べることができます。対応関係はありますが、かなり弱く、相関は 1 よりはるかに小さくなります。
[35]:
import matplotlib.pyplot as plt
plt.rc("figure", figsize=(10, 10))
plt.rc("font", size=14)
_ = plt.scatter(res.resid[:13], eta[200 : 200 + 13])
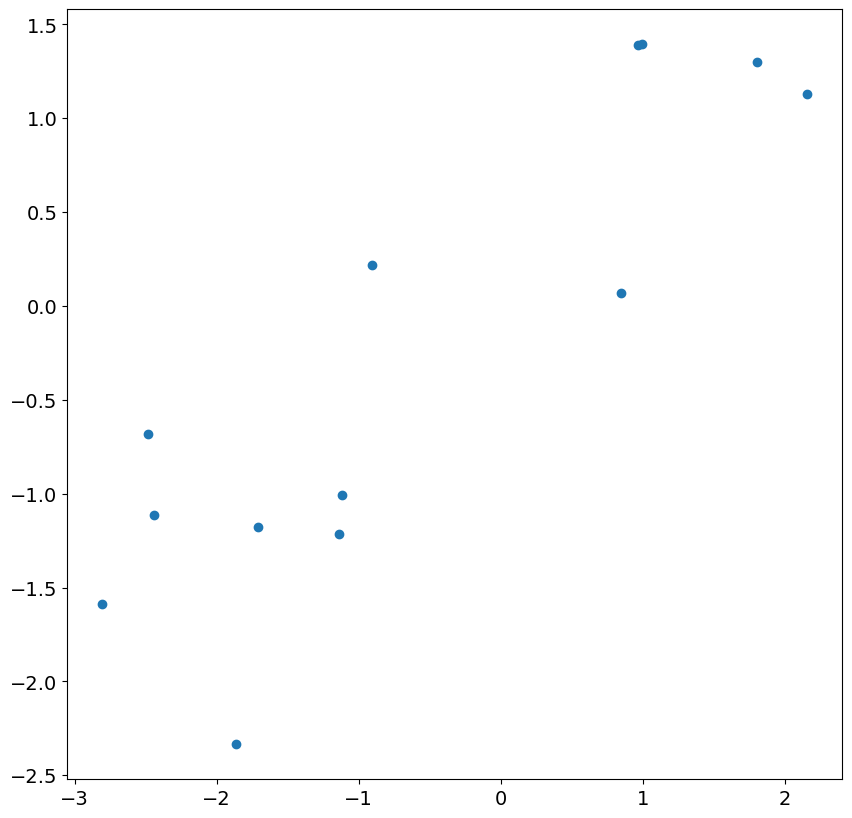
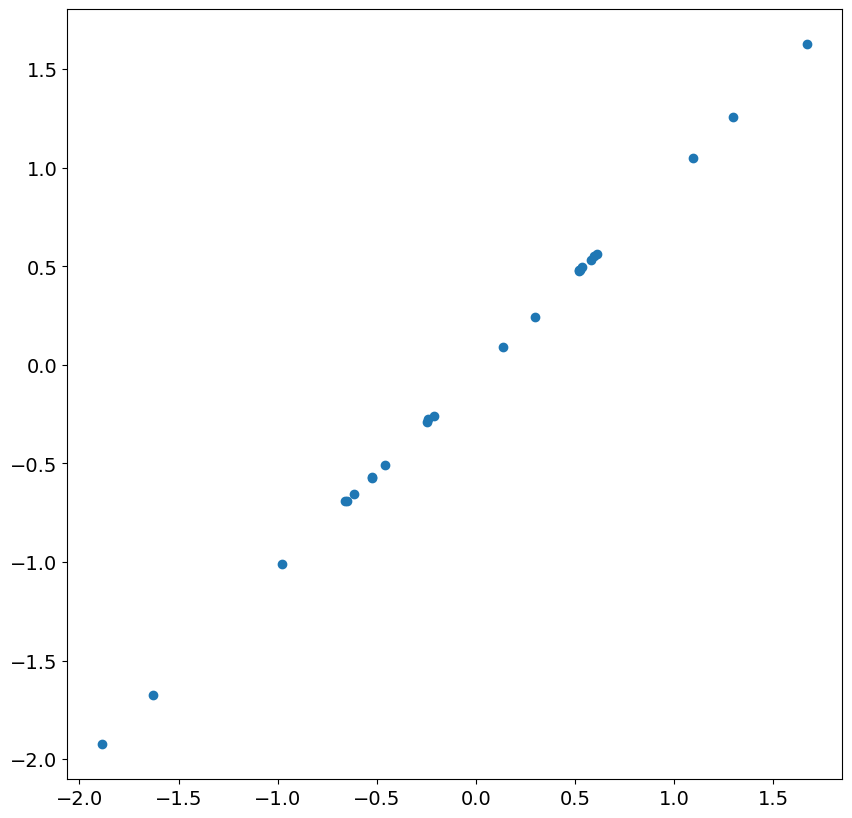
次の 24 個の残差とショックを見ると、ほぼ完全な相関があることがわかります。これは、精度が低い残差が無視されると、大きなサンプルで期待されることです。
[36]:
_ = plt.scatter(res.resid[13:37], eta[200 + 13 : 200 + 37])
次に、ARIMA(1,1,0) をシミュレートし、時間トレンドを含めます。
[37]:
rng = np.random.default_rng(20210819)
eta = rng.standard_normal(5200)
rho = 0.8
beta = 20
epsilon = eta.copy()
for i in range(2, eta.shape[0]):
epsilon[i] = (1 + rho) * epsilon[i - 1] - rho * epsilon[i - 2] + eta[i]
t = np.arange(epsilon.shape[0])
y = beta + 2 * t + epsilon
y = y[200:]
ここでも、パラメータ推定値は DGP パラメータと非常に近くなります。
[38]:
res = ARIMA(y, order=(1, 1, 0), trend="t").fit()
print(res.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 5000
Model: ARIMA(1, 1, 0) Log Likelihood -7067.739
Date: Thu, 03 Oct 2024 AIC 14141.479
Time: 15:45:20 BIC 14161.030
Sample: 0 HQIC 14148.331
- 5000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
x1 1.7747 0.069 25.642 0.000 1.639 1.910
ar.L1 0.7968 0.009 93.658 0.000 0.780 0.813
sigma2 0.9896 0.020 49.908 0.000 0.951 1.028
===================================================================================
Ljung-Box (L1) (Q): 0.43 Jarque-Bera (JB): 0.09
Prob(Q): 0.51 Prob(JB): 0.96
Heteroskedasticity (H): 0.97 Skew: -0.01
Prob(H) (two-sided): 0.47 Kurtosis: 2.99
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
残差は正確ではなく、最初の残差は約 500 です。他の残差はより近いですが、このモデルでは、最初の 2 つの残差は通常無視する必要があります。
[39]:
res.resid[:5]
[39]:
array([ 5.08403002e+02, -1.58904197e+00, -1.54902446e+00, 1.04992617e-01,
1.33644383e+00])
最初の残差がこれほど大きい理由は、この値の最適予測が差の平均である 1.77 であるためです。最初の値がわかると、2 番目の値はその予測に最初の値を使用するため、予測は真実にかなり近くなります。
[40]:
res.predict(0, 5)
[40]:
array([ 1.77472562, 511.95355128, 510.87392196, 508.85708934,
509.03356182, 511.85245439])
結果クラスには、どの残差に問題があるかを理解するのに役立つ 2 つのパラメータ、loglikelihood_burn と nobs_diffuse が含まれていることに注意してください。
[41]:
res.loglikelihood_burn, res.nobs_diffuse
[41]:
(1, 0)
最終更新日: 2024 年 10 月 3 日