デトレンド、様式化された事実、ビジネスサイクル

影響力のある記事の中で、ハーヴェイとイェーガー (1993) は、観測不能成分モデル（別名「構造時系列モデル」）を使用して、ビジネスサイクルの様式化された事実を導き出す方法について述べました。

彼らの論文は、次のように始まります。

"Establishing the 'stylized facts' associated with a set of time series is widely considered a crucial step
in macroeconomic research ... For such facts to be useful they should (1) be consistent with the stochastic
properties of the data and (2) present meaningful information."

特に、彼らは、これらの目標は、一般的な Hodrick-Prescott フィルタや Box-Jenkins ARIMA モデリング手法ではなく、観測不能成分アプローチを使用して達成されることがよくあります。

statsmodels には、3 種類すべての分析を実行する機能があり、以下では、わずかに更新されたデータセットを使用して論文の手順に従います。

[1]:

%matplotlib inline

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

from IPython.display import display, Latex

観測不能成分

statsmodels で使用可能な観測不能成分モデルは次のように書くことができます。

\[y_t = \underbrace{\mu_{t}}_{\text{トレンド}} + \underbrace{\gamma_{t}}_{\text{季節変動}} + \underbrace{c_{t}}_{\text{周期}} + \sum_{j=1}^k \underbrace{\beta_j x_{jt}}_{\text{説明変数}} + \underbrace{\varepsilon_t}_{\text{不規則性}}\]

表記および追加の詳細については、ダビンとクープマンの 2012 年の第 3 章を参照してください。異なる個々の成分に対する異なる仕様は、さまざまなモデルをサポートできることに注意してください。論文および以下で考慮される特定のモデルはこの一般的な方程式の特殊化です。

トレンド

トレンド成分は、切片と線形時系列トレンドを含む回帰モデルの動的な拡張です。

\[\begin{split}\begin{align} \underbrace{\mu_{t+1}}_{\text{レベル}} & = \mu_t + \nu_t + \eta_{t+1} \qquad & \eta_{t+1} \sim N(0, \sigma_\eta^2) \\\\ \underbrace{\nu_{t+1}}_{\text{トレンド}} & = \nu_t + \zeta_{t+1} & \zeta_{t+1} \sim N(0, \sigma_\zeta^2) \\ \end{align}\end{split}\]

レベルがインターセプトタームを一般化したもので、時間とともに動的に変化し、トレンドが時系列トレンドの一般化で、傾きが時間とともに動的に変化します。

両方の要素（レベルとトレンド）において、以下のモデルを検討できます。

  • 要素の含めと除外（トレンドを含める場合は、レベルも含まれている必要があります）。

  • 要素の決定論的と確率的（すなわち、誤差項の分散がゼロに限定されるかどうか）。

MLEによって推定される追加のパラメータは、含まれている確率的構成要素の分散のみです。

これにより、次の仕様が得られます。

レベル

トレンド

確率的レベル

確率的トレンド

定数

✓

ローカルレベル（ランダムウォーク）

✓

✓

決定論的トレンド

✓

✓

決定論的トレンドを伴うローカルレベル（ドリフトを伴うランダムウォーク）

✓

✓

✓

ローカル線形トレンド

✓

✓

✓

✓

スムーズトレンド（積分ランダムウォーク）

✓

✓

✓

季節性

季節成分は次のように記述されます。

\[\gamma_t = - \sum_{j=1}^{s-1} \gamma_{t+1-j} + \omega_t \qquad \omega_t \sim N(0, \sigma_\omega^2)\]

周期（季節の数）はsで、決定的な特徴は（誤差項なしで）季節成分が1つの完全なサイクルでゼロに合計されることです。誤差項を含めることで、季節的な影響が時間とともに変化します。

このモデルのバリエーションは次のとおりです。

  • 周期s

  • 季節の影響を確率的にするかどうかの設定。

季節の影響が確率的な場合、MLEによって推定する追加のパラメータが1つあります（誤差項の分散）。

サイクル

循環成分は、季節成分によってキャプチャされる時間フレームよりもはるかに長い時間フレームの循環効果をキャプチャすることを目的としています。たとえば、経済学では、通常、循環用語はビジネスサイクルをキャプチャすることを意図しており、その後、「1.5年から12年」の間の期間があると予想されています（ダービンとクープマンを参照）。

サイクルは次のように記述されます。

\[\begin{split}\begin{align} c_{t+1} & = c_t \cos \lambda_c + c_t^* \sin \lambda_c + \tilde \omega_t \qquad & \tilde \omega_t \sim N(0, \sigma_{\tilde \omega}^2) \\\\ c_{t+1}^* & = -c_t \sin \lambda_c + c_t^* \cos \lambda_c + \tilde \omega_t^* & \tilde \omega_t^* \sim N(0, \sigma_{\tilde \omega}^2) \end{align}\end{split}\]

パラメータ\(\lambda_c\)（サイクルの周波数）は、MLEによって推定される追加のパラメータです。季節的な効果が確率的な場合、推定されるパラメータが1つあります（誤差項の分散。ここで両方の誤差項は同じ分散を共有しますが、独立描画があると想定されています）。

不規則

不規則成分は白色雑音誤差項であると仮定されます。その分散は、MLEによって推定されるパラメータです。すなわち

\[\varepsilon_t \sim N(0, \sigma_\varepsilon^2)\]

場合によっては、自己回帰効果を考慮するように不規則成分を一般化できます。

\[\varepsilon_t = \rho(L) \varepsilon_{t-1} + \epsilon_t, \qquad \epsilon_t \sim N(0, \sigma_\epsilon^2)\]

この場合、自己回帰パラメータもMLEによって推定されます。

回帰効果

追加の項を含めることで説明変数に対応する場合があります。

\[\sum_{j=1}^k \beta_j x_{jt}\]

または、次を含めることで介入効果に対応します。

\[\begin{split}\begin{align} \delta w_t \qquad \text{where} \qquad w_t & = 0, \qquad t < \tau, \\\\ & = 1, \qquad t \ge \tau \end{align}\end{split}\]

これら追加パラメーターは MLE で推定するか、状態空間定式のコンポーネントとして含めることで推定可能です。

データ

Harvey と Jaeger に倣って次の時系列を検討してみます。

  • 米国の実質 GNP、「産出」（GNPC96）

  • 米国の GNP 暗示価格デフレーター、「価格」（GNPDEF）

  • 米国の通貨ベース、「通貨」（AMBSL）

元の論文での時間枠はシリーズによって異なりますが、概ね 1954 年から 1989 年です。以下ではすべてのシリーズについて、1948 年から 2008 年までのデータを使用します。未観測成分法を使用すると、モデル内で季節成分を分離できますが、この論文やここでは、すでに季節調整されたシリーズが検討されます。

ここで検討するすべてのデータ系列は 連邦準備理事会経済データ (FRED) から取得しています。便利なことに、Python ライブラリの Pandas は FRED からデータを直接ダウンロードできます。

[2]:

# Datasets
from pandas_datareader.data import DataReader

# Get the raw data
start = '1948-01'
end = '2008-01'
us_gnp = DataReader('GNPC96', 'fred', start=start, end=end)
us_gnp_deflator = DataReader('GNPDEF', 'fred', start=start, end=end)
us_monetary_base = DataReader('AMBSL', 'fred', start=start, end=end).resample('QS').mean()
recessions = DataReader('USRECQ', 'fred', start=start, end=end).resample('QS').last().values[:,0]

# Construct the dataframe
dta = pd.concat(map(np.log, (us_gnp, us_gnp_deflator, us_monetary_base)), axis=1)
dta.columns = ['US GNP','US Prices','US monetary base']
dta.index.freq = dta.index.inferred_freq
dates = dta.index._mpl_repr()

これら 3 つの変数の時間的枠組みを把握するために、プロットしてみます。

[3]:

# Plot the data
ax = dta.plot(figsize=(13,3))
ylim = ax.get_ylim()
ax.xaxis.grid()
ax.fill_between(dates, ylim[0]+1e-5, ylim[1]-1e-5, recessions, facecolor='k', alpha=0.1);
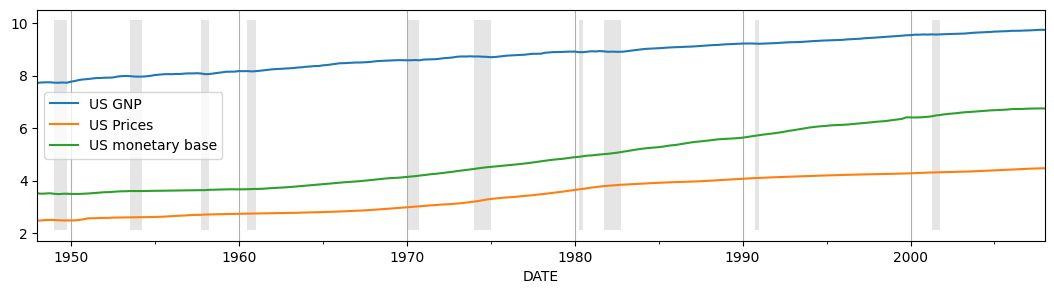
../../../_images/examples_notebooks_generated_statespace_structural_harvey_jaeger_6_0.png

モデル

データはすでに季節調整されており、明白な説明変数がないため、検討する一般的なモデルは以下のとおりです。

\[y_t = \underbrace{\mu_{t}}_{\text{トレンド}} + \underbrace{c_{t}}_{\text{サイクル}} + \underbrace{\varepsilon_t}_{\text{不規則}}\]

不規則はホワイトノイズと仮定され、サイクルは確率的かつ減衰しています。最終的なモデリングの選択は、トレンド成分に使用される仕様です。Harvey と Jaeger では次の 2 つのモデルが検討されます。

  1. ローカル線形トレンド（「無制限」モデル）

  2. スムーズトレンド（\(\sigma_\eta = 0\) を強制しているため、「制限」モデル）

以下に、これらの各モデルタイプの kwargs ディクショナリを作成しています。モデルを指定する方法は 2 つあることに注意してください。1 つは、上の表のようにコンポーネントを直接指定する方法です。もう 1 つは、さまざまな仕様にマップする文字列名を使用する方法です。

[4]:

# Model specifications

# Unrestricted model, using string specification
unrestricted_model = {
    'level': 'local linear trend', 'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True
}

# Unrestricted model, setting components directly
# This is an equivalent, but less convenient, way to specify a
# local linear trend model with a stochastic damped cycle:
# unrestricted_model = {
#     'irregular': True, 'level': True, 'stochastic_level': True, 'trend': True, 'stochastic_trend': True,
#     'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True
# }

# The restricted model forces a smooth trend
restricted_model = {
    'level': 'smooth trend', 'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True
}

# Restricted model, setting components directly
# This is an equivalent, but less convenient, way to specify a
# smooth trend model with a stochastic damped cycle. Notice
# that the difference from the local linear trend model is that
# `stochastic_level=False` here.
# unrestricted_model = {
#     'irregular': True, 'level': True, 'stochastic_level': False, 'trend': True, 'stochastic_trend': True,
#     'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True
# }

ここで、次のモデルにフィットします。

  1. 無制限モデルの産出

  2. 無制限モデルの価格

  3. 制限モデルの価格

  4. 無制限モデルの通貨

  5. 制限モデルの通貨

[5]:

# Output
output_mod = sm.tsa.UnobservedComponents(dta['US GNP'], **unrestricted_model)
output_res = output_mod.fit(method='powell', disp=False)

# Prices
prices_mod = sm.tsa.UnobservedComponents(dta['US Prices'], **unrestricted_model)
prices_res = prices_mod.fit(method='powell', disp=False)

prices_restricted_mod = sm.tsa.UnobservedComponents(dta['US Prices'], **restricted_model)
prices_restricted_res = prices_restricted_mod.fit(method='powell', disp=False)

# Money
money_mod = sm.tsa.UnobservedComponents(dta['US monetary base'], **unrestricted_model)
money_res = money_mod.fit(method='powell', disp=False)

money_restricted_mod = sm.tsa.UnobservedComponents(dta['US monetary base'], **restricted_model)
money_restricted_res = money_restricted_mod.fit(method='powell', disp=False)

これらのモデルにフィットしたら、情報を表示する方法は多数あります。米国の GNP モデルを見ると、フィットの summary メソッドを使用してモデルのフィットをまとめることができます。

[6]:

print(output_res.summary())

                            Unobserved Components Results
=====================================================================================
Dep. Variable:                        US GNP   No. Observations:                  241
Model:                    local linear trend   Log Likelihood                 769.972
                   + damped stochastic cycle   AIC                          -1527.945
Date:                       Thu, 03 Oct 2024   BIC                          -1507.136
Time:                               15:50:16   HQIC                         -1519.558
Sample:                           01-01-1948
                                - 01-01-2008
Covariance Type:                         opg
====================================================================================
                       coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------------
sigma2.irregular  1.399e-06   7.35e-06      0.190      0.849    -1.3e-05    1.58e-05
sigma2.level      2.775e-06   4.97e-05      0.056      0.955   -9.47e-05       0.000
sigma2.trend      3.199e-06   1.48e-06      2.162      0.031    2.99e-07     6.1e-06
sigma2.cycle      3.871e-05   2.55e-05      1.517      0.129   -1.13e-05    8.87e-05
frequency.cycle      0.4496      0.047      9.548      0.000       0.357       0.542
damping.cycle        0.8672      0.042     20.564      0.000       0.785       0.950
===================================================================================
Ljung-Box (L1) (Q):                   0.00   Jarque-Bera (JB):                 9.27
Prob(Q):                              1.00   Prob(JB):                         0.01
Heteroskedasticity (H):               0.26   Skew:                            -0.04
Prob(H) (two-sided):                  0.00   Kurtosis:                         3.97
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

未観測成分モデルの場合、特に序文の (2) 番目のポイントに従って定型的な事実を探索する場合、推定された未観測成分（レベル、トレンド、サイクルなど）自体をプロットして、それらがデータの有意義な記述を提供するかどうかを確認すると、より有益な場合がほとんどです。

フィットオブジェクトの plot_components メソッドを使用して、推定状態のそれぞれのプロットと信頼区間を表示したり、観測されたデータとモデルの 1 ステップ先予測とのプロットを使用してフィットを評価したりできます。

[7]:

fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9));

/opt/hostedtoolcache/Python/3.10.15/x64/lib/python3.10/site-packages/statsmodels/tsa/statespace/structural.py:1738: RuntimeWarning: invalid value encountered in sqrt
  std_errors = np.sqrt(component_bunch['%s_cov' % which])
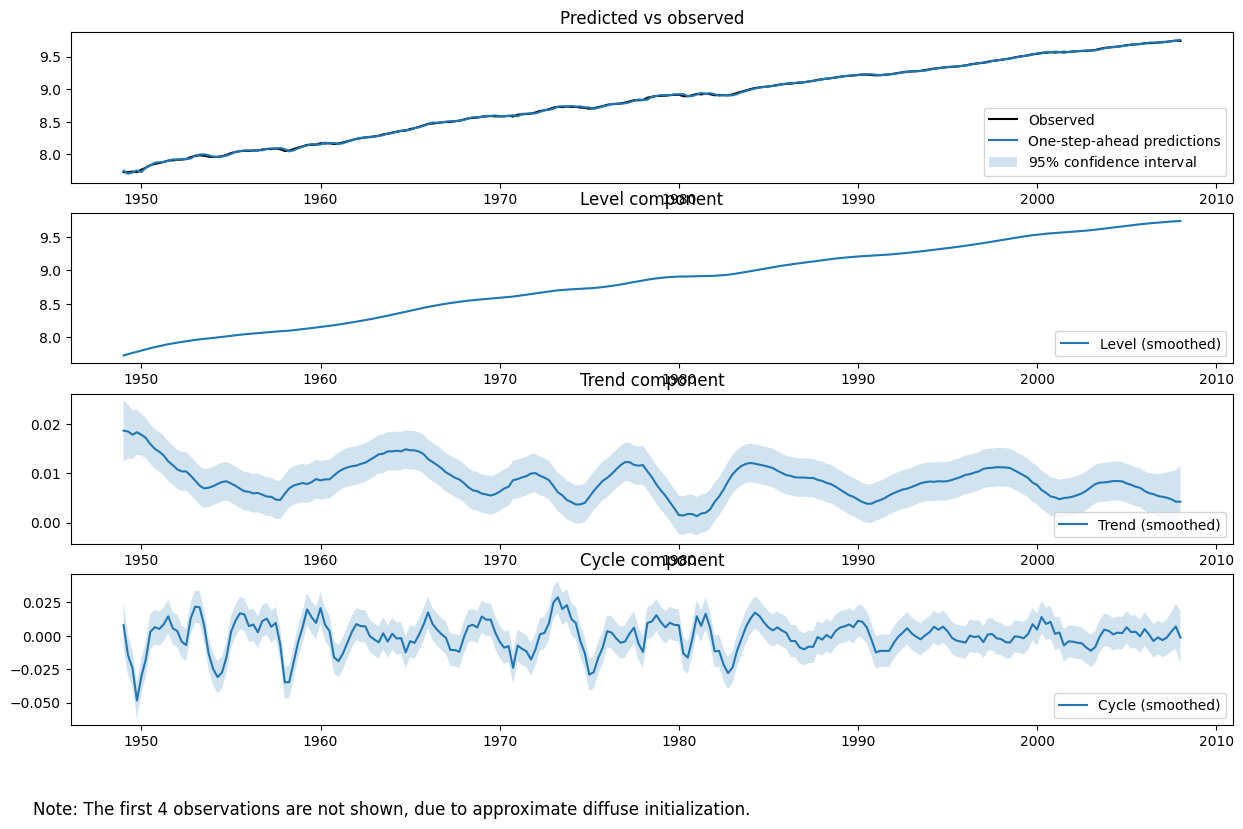
../../../_images/examples_notebooks_generated_statespace_structural_harvey_jaeger_14_1.png

最後に、Harvey と Jaeger はモデルを別の方法でまとめて、トレンドコンポーネントと周期コンポーネントの相対的な重要性を強調しました。以下に、表 I を複製します。私たちが見つけた値は彼らの表の値と概ね一致していますが、細部は異なります。

[8]:

# Create Table I
table_i = np.zeros((5,6))

start = dta.index[0]
end = dta.index[-1]
time_range = '%d:%d-%d:%d' % (start.year, start.quarter, end.year, end.quarter)
models = [
    ('US GNP', time_range, 'None'),
    ('US Prices', time_range, 'None'),
    ('US Prices', time_range, r'$\sigma_\eta^2 = 0$'),
    ('US monetary base', time_range, 'None'),
    ('US monetary base', time_range, r'$\sigma_\eta^2 = 0$'),
]
index = pd.MultiIndex.from_tuples(models, names=['Series', 'Time range', 'Restrictions'])
parameter_symbols = [
    r'$\sigma_\zeta^2$', r'$\sigma_\eta^2$', r'$\sigma_\kappa^2$', r'$\rho$',
    r'$2 \pi / \lambda_c$', r'$\sigma_\varepsilon^2$',
]

i = 0
for res in (output_res, prices_res, prices_restricted_res, money_res, money_restricted_res):
    if res.model.stochastic_level:
        (sigma_irregular, sigma_level, sigma_trend,
         sigma_cycle, frequency_cycle, damping_cycle) = res.params
    else:
        (sigma_irregular, sigma_level,
         sigma_cycle, frequency_cycle, damping_cycle) = res.params
        sigma_trend = np.nan
    period_cycle = 2 * np.pi / frequency_cycle

    table_i[i, :] = [
        sigma_level*1e7, sigma_trend*1e7,
        sigma_cycle*1e7, damping_cycle, period_cycle,
        sigma_irregular*1e7
    ]
    i += 1

pd.set_option('float_format', lambda x: '%.4g' % np.round(x, 2) if not np.isnan(x) else '-')
table_i = pd.DataFrame(table_i, index=index, columns=parameter_symbols)
table_i

[8]:
$\sigma_\zeta^2$ $\sigma_\eta^2$ $\sigma_\kappa^2$ $\rho$ $2 \pi / \lambda_c$ $\sigma_\varepsilon^2$
時系列 時間範囲 制約
米国国民総生産 1948:1-2008:1 なし 27.75 31.99 387.1 0.87 13.98 13.99
米国物価 1948:1-2008:1 なし 0 61.88 20.71 0.43 6.55 0
$\sigma_\eta^2 = 0$ 61.92 NaN 20.69 0.43 6.55 0
米国の金融ベース 1948:1-2008:1 なし 68.75 18.86 192.7 0.89 23.19 0
$\sigma_\eta^2 = 0$ 18.92 NaN 247.1 0.89 23.8 0
最終更新: 2024年10月03日